5.14 - Exercícios

Exercício 5.1

O módulo time fornece uma função, também chamada time, que devolve a Hora Média de Greenwich na “época”, que é um momento arbitrário usado como ponto de referência. Em sistemas UNIX, a época é primeiro de janeiro de 1970.

>>> import time
>>> time.time()
1437746094.5735958

Escreva um script que leia a hora atual e a converta em um tempo em horas, minutos e segundos, mais o número de dias desde a época.

Exercício 5.2

O último teorema de Fermat diz que não existem números inteiros a, b e c tais que a**n + b**n == c**n para quaisquer valores de n maiores que 2.

  1. Escreva uma função chamada check_fermat que receba quatro parâmetros – a, b, c e n – e verifique se o teorema de Fermat se mantém. Se n for maior que 2 e a**n + b**n == c**n o programa deve imprimir, “Holy smokes, Fermat was wrong!” Senão o programa deve exibir “No, that doesn’t work.”

  2. Escreva uma função que peça ao usuário para digitar valores para a, b, c e n, os converta em números inteiros e use check_fermat para verificar se violam o teorema de Fermat.

Exercício 5.3

Se você tiver três gravetos, pode ser que consiga arranjá-los em um triângulo ou não. Por exemplo, se um dos gravetos tiver 12 polegadas de comprimento e outros dois tiverem uma polegada de comprimento, não será possível fazer com que os gravetos curtos se encontrem no meio. Há um teste simples para ver se é possível formar um triângulo para quaisquer três comprimentos:

Se algum dos três comprimentos for maior que a soma dos outros dois, então você não pode formar um triângulo. Senão, você pode. (Se a soma de dois comprimentos igualar o terceiro, eles formam um triângulo chamado “degenerado”)

  1. Escreva uma função chamada is_triangle que receba três números inteiros como argumentos, e que imprima “Yes” ou “No”, dependendo da possibilidade de formar ou não um triângulo de gravetos com os comprimentos dados.

  2. Escreva uma função que peça ao usuário para digitar três comprimentos de gravetos, os converta em números inteiros e use is_triangle para verificar se os gravetos com os comprimentos dados podem formar um triângulo.

Exercício 5.4

Qual é a saída do seguinte programa? Desenhe um diagrama da pilha que mostre o estado do programa quando exibir o resultado.

def recurse(n, s):
    if n == 0:
        print(s)
    else:
        recurse(n-1, n+s)

recurse(3, 0)

  1. O que aconteceria se você chamasse esta função desta forma: recurse(-1, 0)?

  2. Escreva uma docstring que explique tudo o que alguém precisaria saber para usar esta função (e mais nada).

Os seguintes exercícios usam o módulo turtle, descrito no Capítulo 4:

Exercício 5.5

Leia a próxima função e veja se consegue compreender o que ela faz (veja os exemplos no Capítulo 4). Então execute-a e veja se acertou.

def draw(t, length, n):
    if n == 0:
        return
    angle = 50
    t.fd(length * n)
    t.lt(angle)
    draw(t, length, n-1)
    t.rt(2 * angle)
    draw(t, length, n-1)
    t.lt(angle)
    t.bk(length * n)

Exercício 5.6

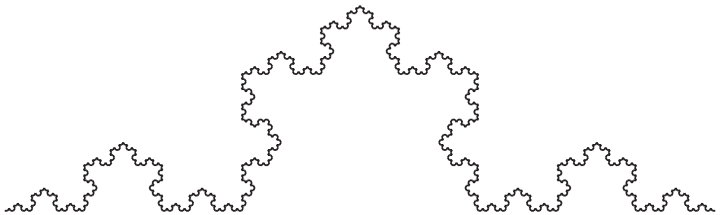Figura 5.2 – Uma curva de Koch.
Figura 5.2 – Uma curva de Koch.

A curva de Koch é um fractal que parece com o da Figura 5.2. Para desenhar uma curva de Koch com o comprimento x, tudo o que você tem que fazer é:

  1. Desenhe uma curva de Koch com o comprimento x/3.

  2. Vire 60 graus à esquerda.

  3. Desenhe uma curva de Koch com o comprimento x/3.

  4. Vire 120 graus à direita.

  5. Desenhe uma curva de Koch com o comprimento x/3.

  6. Vire 60 graus à esquerda.

  7. Desenhe uma curva de Koch com o comprimento x/3.

A exceção é se x for menor que 3: neste caso, você pode desenhar apenas uma linha reta com o comprimento x.

  1. Escreva uma função chamada koch que receba um turtle e um comprimento como parâmetros, e use o turtle para desenhar uma curva de Koch com o comprimento dado.

  2. Escreva uma função chamada snowflake que desenhe três curvas de Koch para fazer o traçado de um floco de neve.

        Solução: http://thinkpython2.com/code/koch.py.

  1. A curva de Koch pode ser generalizada de vários modos. Veja exemplos em http://en.wikipedia.org/wiki/Koch_snowflake e implemente o seu favorito.