11.6 - Memos
Se usou a função de fibonacci em “Mais um exemplo”, na página 101, pode ter notado que quanto maior o argumento dado mais tempo a função leva para ser executada. Além disso, o tempo de execução aumenta rapidamente.
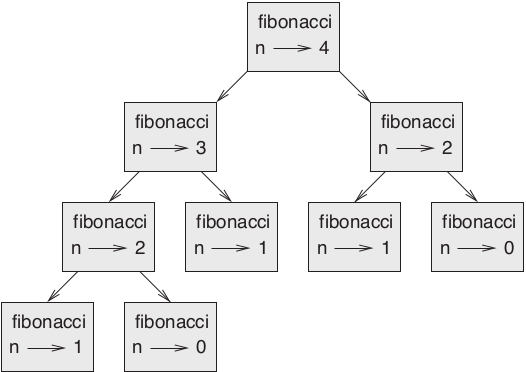
Para entender por que, considere a Figura 11.2, que mostra o gráfico de chamada de fibonacci com n=4.
 .
.
Figura 11.2 – Gráfico de chamada para fibonacci.
Um gráfico de chamada mostra um conjunto de frames de função, com linhas que unem cada frame aos frames das funções que chama. Na parte de cima do gráfico, fibonacci com n=4 chama fibonacci com n=3 e n=2. Por sua vez, fibonacci com n=3 chama fibonacci com n=2 e n=1. E assim por diante.
Conte quantas vezes fibonacci(0) e fibonacci(1) são chamadas. Essa é uma solução ineficiente para o problema, e piora conforme o argumento se torna maior.
Uma solução é acompanhar os valores que já foram calculados, guardando-os em um dicionário. Um valor calculado anteriormente que é guardado para uso posterior é chamado de memo. Aqui está uma versão com memos de fibonacci:
known = {0:0, 1:1}
def fibonacci(n):
if n in known:
return known[n]
res = fibonacci(n-1) + fibonacci(n-2)
known[n] = res
return res
known é um dicionário que monitora os números de Fibonacci que já conhecemos. Começa com dois itens: 0 mapeia a 0 e 1 mapeia a 1.
Sempre que fibonacci é chamada, ela verifica known. Se o resultado já estiver lá, pode voltar imediatamente. Se não for o caso, é preciso calcular o novo valor, acrescentá-lo ao dicionário e devolvê-lo.
Se você executar essa versão de fibonacci e a comparar com a original, descobrirá que é muito mais rápida.