Pense em Python

6.11 - Exercícios

Exercício 6.1

Desenhe um diagrama da pilha do seguinte programa. O que o programa exibe?

def b(z):
    prod = a(z, z)
    print(z, prod)
    return prod

def a(x, y):
    x = x + 1
    return x * y

def c(x, y, z):
    total = x + y + z
    square = b(total)**2
    return square

x = 1
y = x + 1
print(c(x, y+3, x+y))

Exercício 6.2

A função de Ackermann, A(m, n), é definida assim:

.

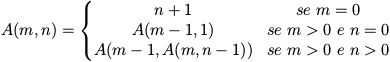Veja http://en.wikipedia.org/wiki/Ackermann_function. Escreva uma função denominada ack que avalie a função de Ackermann. Use a sua função para avaliar ack(3, 4), cujo resultado deve ser 125. O que acontece para valores maiores de m e n?

Solução: http://thinkpython2.com/code/ackermann.py.

Exercício 6.3

Um palíndromo é uma palavra que se soletra da mesma forma nos dois sentidos, como “osso” e “reviver”. Recursivamente, uma palavra é um palíndromo se a primeira e última letras forem iguais e o meio for um palíndromo.

As funções seguintes recebem uma string como argumento e retornam as letras iniciais, finais e do meio das palavras:

def first(word):
    return word[0]
def last(word):
    return word[-1]
def middle(word):
    return word[1:-1]

Veremos como funcionam no Capítulo 8.

1. Digite essas funções em um arquivo chamado palindrome.py e teste-as. O que acontece se chamar middle com uma string de duas letras? Uma letra? E se a string estiver vazia, escrita com '' e não contiver nenhuma letra?

2. Escreva uma função chamada is_palindrome que receba uma string como argumento e retorne True se for um palíndromo e False se não for. Lembre-se de que você pode usar a função integrada len para verificar o comprimento de uma string.

Solução: http://thinkpython2.com/code/palindrome_soln.py.

Exercício 6.4

Um número a é uma potência de b se for divisível por b e a/b for uma potência de b. Escreva uma função chamada is_power que receba os parâmetros a e b e retorne True se a for uma potência de b. Dica: pense no caso-base.

Exercício 6.5

O maior divisor comum (MDC, ou GCD em inglês) de a e b é o maior número que divide ambos sem sobrar resto.

Um modo de encontrar o MDC de dois números é observar qual é o resto r quando a é dividido por b, verificando que gcd(a, b) = gcd(b, r). Como caso-base, podemos usar gcd(a, 0) = a.

Escreva uma função chamada gcd que receba os parâmetros a e b e devolva o maior divisor comum.

Crédito: Este exercício é baseado em um exemplo do livro de Abelson e Sussman, Structure and Interpretation of Computer Programs (Estrutura e interpretação de programas de computador, MIT Press, 1996).