7.9 - Exercícios
Exercício 7.1
Copie o loop de “Raízes quadradas”, na página 111, e encapsule-o em uma função chamada mysqrt que receba a como parâmetro, escolha um valor razoável de x e devolva uma estimativa da raiz quadrada de a.
Para testar, escreva uma função denominada test_square_root, que exibe uma tabela como esta:
a mysqrt(a) math.sqrt(a) diff
- --------- ------------ ----
1.0 1.0 1.0 0.0
2.0 1.41421356237 1.41421356237 2.22044604925e-16
3.0 1.73205080757 1.73205080757 0.0
4.0 2.0 2.0 0.0
5.0 2.2360679775 2.2360679775 0.0
6.0 2.44948974278 2.44948974278 0.0
7.0 2.64575131106 2.64575131106 0.0
8.0 2.82842712475 2.82842712475 4.4408920985e-16
9.0 3.0 3.0 0.0
A primeira coluna é um número, a; a segunda coluna é a raiz quadrada de a calculada com mysqrt; a terceira coluna é a raiz quadrada calculada por math.sqrt; a quarta coluna é o valor absoluto da diferença entre as duas estimativas.
Exercício 7.2
A função integrada eval toma uma string e a avalia, usando o interpretador do Python. Por exemplo:
>>> eval('1 + 2 * 3')
7
>>> import math
>>> eval('math.sqrt(5)')
2.2360679774997898
>>> eval('type(math.pi)')
<class 'float'>
Escreva uma função chamada eval_loop que iterativamente peça uma entrada ao usuário, a avalie usando eval e exiba o resultado.
Ela deve continuar até que o usuário digite done; então deverá exibir o valor da última expressão avaliada.
Exercício 7.3
O matemático Srinivasa Ramanujan encontrou uma série infinita que pode ser usada para gerar uma aproximação numérica de 1/π:
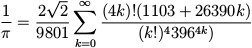 .
.
Escreva uma função chamada estimate_pi que use esta fórmula para computar e devolver uma estimativa de π. Você deve usar o loop while para calcular os termos da adição até que o último termo seja menor que 1e-15 (que é a notação do Python para 10 ** 15). Você pode verificar o resultado comparando-o com math.pi.