6.2 - Desenvolvimento incremental
Conforme você escrever funções maiores, pode ser que passe mais tempo as depurando.
Para lidar com programas cada vez mais complexos, você pode querer tentar usar um processo chamado de desenvolvimento incremental. A meta do desenvolvimento incremental é evitar longas sessões de depuração, acrescentando e testando pequenas partes do código de cada vez.
Como um exemplo, vamos supor que você queira encontrar a distância entre dois pontos dados pelas coordenadas (x1, y1) e(x2, y2). Pelo teorema de Pitágoras, a distância é:
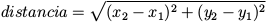 .
.
O primeiro passo é pensar como uma função distance deveria ser no Python. Em outras palavras, quais são as entradas (parâmetros) e qual é a saída (valor de retorno)?
Nesse caso, as entradas são dois pontos que você pode representar usando quatro números. O valor de retorno é a distância representada por um valor de ponto flutuante.
Imediatamente, é possível escrever um rascunho da função:
def distance(x1, y1, x2, y2):
return 0.0
Claro que esta versão não calcula distâncias; sempre retorna zero. Mas está sintaticamente correta, e pode ser executada, o que significa que você pode testá-la antes de torná-la mais complicada.
Para testar a nova função, chame-a com argumentos de amostra:
>>> distance(1, 2, 4, 6)
0.0
Escolhi esses valores para que a distância horizontal seja 3 e a distância vertical, 4; assim, o resultado final é 5, a hipotenusa de um triângulo 3-4-5. Ao testar uma função, é útil saber a resposta certa.
Neste ponto confirmamos que a função está sintaticamente correta, e podemos começar a acrescentar código ao corpo. Um próximo passo razoável é encontrar as diferenças x2 − x1 e y2 − y1. A próxima versão guarda esses valores em variáveis temporárias e os exibe:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
print('dx is', dx)
print('dy is', dy)
return 0.0
Se a função estiver funcionando, deve exibir dx is 3 e dy is 4. Nesse caso sabemos que a função está recebendo os argumentos corretos e executando o primeiro cálculo acertadamente. Se não, há poucas linhas para verificar.
Depois calculamos a soma dos quadrados de dx e dy:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
print('dsquared is: ', dsquared)
return 0.0
Nesta etapa você executaria o programa mais uma vez e verificaria a saída (que deve ser 25). Finalmente, pode usar math.sqrt para calcular e devolver o resultado:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
result = math.sqrt(dsquared)
return result
Se funcionar corretamente, pronto. Senão, uma ideia é exibir o valor result antes da instrução de retorno.
A versão final da função não exibe nada ao ser executada; apenas retorna um valor. As instruções print que escrevemos são úteis para depuração, mas assim que conferir se a função está funcionando você deve retirá-las. Códigos desse tipo são chamados de scaffolding (andaime) porque são úteis para construir o programa, mas não são parte do produto final.
Ao começar, você deveria acrescentar apenas uma linha ou duas de código de cada vez. Conforme adquira mais experiência, poderá escrever e depurar parcelas maiores. De qualquer forma, o desenvolvimento incremental pode economizar muito tempo de depuração.
Os principais aspectos do processo são:
-
Comece com um programa que funcione e faça pequenas alterações incrementais. Se houver um erro em qualquer ponto, será bem mais fácil encontrá-lo.
-
Use variáveis para guardar valores intermediários, assim poderá exibi-los e verificá-los.
-
Uma vez que o programa esteja funcionando, você pode querer remover uma parte do scaffolding ou consolidar várias instruções em expressões compostas, mas apenas se isso não tornar o programa difícil de ler.
Como exercício, use o desenvolvimento incremental para escrever uma função chamada hypotenuse, que devolva o comprimento da hipotenusa de um triângulo retângulo dados os comprimentos dos outros dois lados como argumentos. Registre cada etapa do processo de desenvolvimento no decorrer do processo.