Pense em Python
Pense como um cientista da computação

Este livro ensina programação para quem nunca programou, usando Python 3 nos exemplos. É aplicado no Olin College, IBMEC e outras faculdades de engenharia de primeira linha.
DICA: Você pode comprar um exemplar impresso de Pense em Python no site da Editora Novatec ou em livrarias. ISBN: 978-85-7522-508-0.
Pense em Python é uma tradução do livro Think Python (2ª edição), de Allen B. Downey, traduzido e publicado no Brasil pela Editora Novatec sob licença da O'Reilly Media.
Créditos da edição brasileira
Editor: Rubens Prates
Tradução: Sheila Gomes
Revisão Gramatical: Smirna Cavalheiro
Editoração Eletrônica: Carolina Kuwabata
Assistente Editorial: Priscila A. Yoshimatsu
Histórico
Allen Downey publicou o original em inglês sob uma licença Creative Commons Atribuição-NãoComercial CC BY-NC 3.0. A Novatec oferece à comunidade esta tradução nos termos da mesma licença do original, CC BY-NC 3.0, atendendo ao desejo do autor oferecer seu trabalho através de uma licença livre.
Esta versão digital de Pense em Python em português foi gerada por Luciano Ramalho da ThoughtWorks a partir de arquivos cedidos por Rubens Prates da Editora Novatec.
Prefácio
A estranha história deste livro
Em janeiro de 1999 eu me preparava para dar aula a uma turma de programação introdutória em Java. Já tinha dado esse curso três vezes e estava ficando frustrado. O índice de aprovação era muito baixo e mesmo entre os alunos aprovados, o nível geral das notas era baixo demais.
Um dos problemas que eu via eram os livros. Eram muito grandes, com detalhes desnecessários sobre o Java, e não havia orientação de alto nível sobre como programar. E todos eles sofriam do efeito alçapão: no início era fácil, os alunos iam aprendendo aos poucos, e lá pelo Capítulo 5, perdiam o chão. Era muito material novo, muito rápido, e eles acabavam engatinhando no resto do semestre.
Duas semanas antes do primeiro dia de aula, eu decidi escrever meu próprio livro. Meus objetivos eram:
-
que o livro fosse curto. Era melhor os alunos lerem 10 páginas que não lerem 50.
-
abordar o vocabulário com cuidado. Tentei minimizar o jargão e definir cada termo no momento do primeiro uso.
-
construir o aprendizado passo a passo. Para evitar alçapões, dividi os tópicos mais difíceis e em uma série de etapas menores.
-
que o conteúdo fosse concentrado em programar mesmo, não na linguagem de programação. Selecionei um subconjunto mínimo útil do Java e omiti o resto.
Eu precisava de um título, então, por capricho, decidi chamá-lo de Pense como um cientista da computação.
A minha primeira versão era apenas um esboço, mas funcionou. Os alunos liam e entendiam o suficiente para podermos usar o tempo de aula para os tópicos difíceis, interessantes e (o mais importante) para permitir que os alunos praticassem.
Lancei o livro sob uma Licença de Documentação Livre GNU, que permite aos usuários copiar, modificar e distribuir o livro.
E o que aconteceu em seguida foi legal. Jeff Elkner, um professor de ensino médio na Virgínia adotou meu livro e o traduziu para Python. Ele me enviou uma cópia de sua tradução e tive a experiência excepcional de aprender Python lendo o meu próprio livro. Com a editora Green Tea, publiquei a primeira versão em Python em 2001.
Em 2003 comecei a trabalhar no Olin College e a ensinar Python pela primeira vez na vida. O contraste com o Java era notável. Os estudantes tinham menos dificuldades, aprendiam mais, trabalhavam em projetos mais interessantes e geralmente se divertiam muito mais.
Desde então continuei a desenvolver o livro, corrigindo erros, melhorando alguns exemplos e acrescentando material, especialmente exercícios.
O resultado está aqui, agora com o título menos grandioso de Pense em Python. Fiz algumas alterações:
-
Acrescentei uma seção sobre depuração (debugging) no fim de cada capítulo. Essas seções apresentam técnicas gerais para encontrar e evitar bugs (erros de programação) e avisos sobre armadilhas do Python.
-
Acrescentei exercícios, incluindo testes curtos de compreensão e alguns projetos substanciais. A maior parte dos exercícios tem um link para a minha solução.
-
Acrescentei uma série de estudos de caso – exemplos mais longos com exercícios, soluções e discussões.
-
Expandi a discussão sobre planos de desenvolvimento de programas e padrões de design básicos.
-
Acrescentei apêndices sobre depuração e análise de algoritmos.
Esta edição de Pense em Python tem as seguintes novidades:
-
O livro e todo o código de apoio foram atualizados para o Python 3.
-
Acrescentei algumas seções e mais detalhes sobre a web, para ajudar os principiantes a executar o Python em um navegador, e não ter que lidar com a instalação do programa até que seja necessário.
-
Para “Módulo turtle” troquei meu próprio pacote gráfico turtle, chamado Swampy, para um módulo Python mais padronizado, turtle, que é mais fácil de instalar e mais eficiente.
-
Acrescentei um novo capítulo chamado “Extra”, que introduz alguns recursos adicionais do Python, não estritamente necessários, mas às vezes práticos.
Espero que goste de trabalhar com este livro, e que ele o ajude a aprender a programar e pensar, pelo menos um pouquinho, como um cientista da computação.
Allen B. Downey
Olin College
Convenções usadas neste livro
As seguintes convenções tipográficas são usadas neste livro:
Itálico
Indica novos termos, URLs, endereços de email, nomes de arquivo e extensões de arquivo.
Negrito
Indica termos definidos no glossário no final de capítulo.
Monoespaçado
Usada para código de programa, bem como dentro de parágrafos para referir-se a elementos do programa, como nomes de variáveis ou de funções, bancos de dados, tipos de dados, variáveis de ambiente, instruções e palavras-chave.
Monoespaçado negrito
Exibe comandos ou outros textos que devem ser digitados literalmente pelo usuário.
Monoespaçado itálico
Exibe textos que devem ser substituídos por valores fornecidos pelos usuários ou por valores determinados pelo contexto.
Uso do código dos exemplos (de acordo com a política da O'Reilly)
Há material suplementar (exemplos de código, exercícios etc) disponível para baixar em http://www.greenteapress.com/thinkpython2/code.
Este livro serve para ajudar você a fazer o que precisa. Em geral, se o livro oferece exemplos de código, você pode usá-los nos seus programas e documentação. Não é preciso entrar em contato conosco para pedir permissão, a menos que esteja reproduzindo uma porção significativa do código. Por exemplo, escrever um programa que use vários pedaços de código deste livro não exige permissão. Vender ou distribuir um CD-ROM de exemplos dos livros da O’Reilly exige permissão. Responder a uma pergunta citando este livro e reproduzindo exemplos de código não exige permissão. Incorporar uma quantidade significativa de exemplos de código deste livro na documentação do seu produto exige permissão.
Agradecemos, mas não exigimos, crédito. O crédito normalmente inclui o título, o autor, a editora e o ISBN. Por exemplo: “Pense em Python, 2ª edição, por Allen B. Downey (O’Reilly). Copyright 2016 Allen Downey, 978-1-4919-3936-9.”
Se acreditar que o seu uso dos exemplos de código não se ajusta à permissão dada anteriormente, fique à vontade para entrar em contato conosco pelo email permissions@oreilly.com.
Como entrar em contato conosco
Envie comentários e dúvidas sobre este livro à editora, escrevendo para: novatec@novatec.com.br.
Temos uma página web para este livro na qual incluímos erratas, exemplos e quaisquer outras informações adicionais.
- Página da edição em português
http://www.novatec.com.br/catalogo/7522508-pense-em-python
- Página da edição original em inglês
Para obter mais informações sobre os livros da Novatec, acesse nosso site em http://www.novatec.com.br.
Agradecimentos
Muito obrigado a Jeff Elkner, que traduziu meu livro de Java para o Python, o que deu início a este projeto e me apresentou ao que acabou sendo a minha linguagem favorita.
Agradeço também a Chris Meyers, que contribuiu em várias seções do Pense como um cientista da computação.
Obrigado à Fundação do Software Livre pelo desenvolvimento da Licença de Documentação Livre GNU, que me ajudou a tornar possível a colaboração com Jeff e Chris, e ao Creative Commons pela licença que estou usando agora.
Obrigado aos editores do Lulu, que trabalharam no Pense como um cientista da computação.
Obrigado aos editores da O’Reilly Media, que trabalharam no Pense em Python.
Obrigado a todos os estudantes que trabalharam com versões anteriores deste livro e a todos os contribuidores (listados a seguir) que enviaram correções e sugestões.
Lista de contribuidores
Mais de cem leitores perspicazes e atentos enviaram sugestões e correções nos últimos anos. Suas contribuições e entusiasmo por este projeto foram inestimáveis.
Se tiver alguma sugestão ou correção, por favor, envie um email a feedback@thinkpython.com. Se eu fizer alguma alteração baseada no seu comentário, acrescentarei seu nome à lista de contribuidores (a menos que você peça para eu omitir a informação).
Se você incluir pelo menos uma parte da frase onde o erro aparece, é mais fácil para eu procurá-lo. Também pode ser o número da página e seção, mas aí é um pouquinho mais difícil de encontrar o erro a ser corrigido. Obrigado!
-
Lloyd Hugh Allen enviou uma correção da Seção 8.4.
-
Yvon Boulianne enviou a correção de um erro semântico no Capítulo 5.
-
Fred Bremmer enviou uma correção da Seção 2.1.
-
Jonah Cohen escreveu os scripts em Perl para converter a fonte de LaTeX deste livro para o belo HTML.
-
Michael Conlon enviou uma correção gramatical do Capítulo 2 e uma melhoria no estilo do Capítulo 1, além de iniciar a discussão sobre os aspectos técnicos de interpretadores.
-
Benoit Girard enviou uma correção a um erro humorístico na Seção 5.6.
-
Courtney Gleason e Katherine Smith escreveram horsebet.py, que foi usado como um estudo de caso em uma versão anterior do livro. O programa agora pode ser encontrado no site.
-
Lee Harr enviou mais correções do que temos espaço para relacionar aqui, e na verdade ele deve ser apontado como um dos editores principais do texto.
-
James Kaylin é um estudante que usa o texto. Ele enviou várias correções.
-
David Kershaw corrigiu a função catTwice defeituosa na Seção 3.10.
-
Eddie Lam entregou diversas correções aos Capítulos 1, 2, e 3. Ele também corrigiu o Makefile para criar um índice na primeira vez que rodar e nos ajudou a estabelecer um esquema de versionamento.
-
Man-Yong Lee enviou uma correção do código de exemplo na Seção 2.4.
-
David Mayo indicou que a palavra “inconscientemente” no Capítulo 1 devia ser alterada para “subconscientemente”.
-
Chris McAloon enviou várias correções para as Seções 3.9 e 3.10.
-
Matthew J. Moelter tem contribuído já há um bom tempo e entregou diversas correções e sugestões para o livro.
-
Simon Dicon Montford informou que havia uma definição de função ausente e vários erros de ortografia no Capítulo 3. Ele também encontrou erros na função increment no Capítulo 13.
-
John Ouzts corrigiu a definição de “valor de retorno” no Capítulo 3.
-
Kevin Parks enviou comentários e sugestões valiosos para melhorar a distribuição do livro.
-
David Pool encontrou um erro de ortografia no glossário do Capítulo 1, e também enviou palavras gentis de encorajamento.
-
Michael Schmitt enviou uma correção ao capítulo sobre arquivos e exceções.
-
Robin Shaw indicou um erro na Seção 13.1, onde a função printTime foi usada em um exemplo sem ser definida.
-
Paul Sleigh encontrou um erro no Capítulo 7 e um bug no script em Perl de Jonah Cohen, que gera o HTML do LaTeX.
-
Craig T. Snydal está testando o texto em um curso na Drew University. Ele contribuiu com várias sugestões valiosas e correções.
-
Ian Thomas e seus alunos estão usando o texto em um curso de programação. Eles são os primeiros a testar os capítulos da segunda metade do livro e fizeram muitas correções e sugestões.
-
Keith Verheyden enviou uma correção no Capítulo 3.
-
Peter Winstanley nos avisou sobre um erro antigo no latim do Capítulo 3.
-
Chris Wrobel fez correções ao código no capítulo sobre arquivos E/S e exceções.
-
Moshe Zadka fez contribuições inestimáveis para este projeto. Além de escrever o primeiro rascunho do capítulo sobre Dicionários, ele forneceu orientação contínua nas primeiras etapas do livro.
-
Christoph Zwerschke enviou várias correções e sugestões pedagógicas, e explicou a diferença entre gleich e selbe.
-
James Mayer enviou-nos um monte de erros tipográficos e ortográficos, inclusive dois da lista de contribuidores.
-
Hayden McAfee percebeu uma inconsistência potencialmente confusa entre dois exemplos.
-
Angel Arnal faz parte de uma equipe internacional de tradutores que trabalhou na versão do texto para o espanhol. Ele também encontrou vários erros na versão em inglês.
-
Tauhidul Hoque e Lex Berezhny criaram as ilustrações do Capítulo 1 e melhoraram muitas das outras ilustrações.
-
O Dr. Michele Alzetta pegou um erro no Capítulo 8 e enviou alguns comentários pedagógicos interessantes e sugestões sobre Fibonacci e o jogo do Mico.
-
Andy Mitchell pegou um erro de ortografia no Capítulo 1 e um exemplo ruim no Capítulo 2.
-
Kalin Harvey sugeriu um esclarecimento no Capítulo 7 e achou alguns erros de ortografia.
-
Christopher P. Smith encontrou vários erros de ortografia e ajudou-nos a atualizar o livro para o Python 2.2.
-
David Hutchins encontrou um erro de ortografia no prefácio.
-
Gregor Lingl é professor de Python em uma escola de Ensino Médio em Viena, na Áustria. Ele está trabalhando em uma tradução do livro para o alemão e encontrou alguns erros feios no Capítulo 5.
-
Julie Peters achou um erro de ortografia no prefácio.
-
Florin Oprina enviou uma melhoria para o makeTime, uma correção no printTime e um belo erro de ortografia.
-
D. J. Webre sugeriu um esclarecimento no Capítulo 3.
-
Ken encontrou um punhado de erros nos Capítulos 8, 9 e 11.
-
Ivo Wever achou um erro de ortografia no Capítulo 5 e sugeriu um esclarecimento no Capítulo 3.
-
Curtis Yanko sugeriu um esclarecimento no Capítulo 2.
-
Ben Logan enviou vários erros de ortografia e problemas com a tradução do livro para HTML.
-
Jason Armstrong percebeu que faltava uma palavra no Capítulo 2.
-
Louis Cordier notou um ponto no Capítulo 16 onde o código não correspondia com o texto.
-
Brian Caim sugeriu vários esclarecimentos nos Capítulos 2 e 3.
-
Rob Black entregou um monte de correções, inclusive algumas alterações para Python 2.2.
-
Jean-Philippe Rey, da École Centrale Paris, enviou uma série de patches, inclusive algumas atualizações do Python 2.2 e outras melhorias bem pensadas.
-
Jason Mader, da George Washington University, fez uma série de sugestões e correções úteis.
-
Jan Gundtofte-Bruun nos lembrou de que “un erro” é um erro.
-
Abel David e Alexis Dinno nos lembraram de que o plural de “matriz” é “matrizes”, não “matrixes”. Este erro esteve no livro por anos, mas dois leitores com as mesmas iniciais informaram a respeito dele no mesmo dia. Bizarro.
-
Charles Thayer nos estimulou a sumir com os pontos e vírgulas que tínhamos posto no final de algumas instruções e a otimizar nosso uso de “argumento” e “parâmetro”.
-
Roger Sperberg indicou uma parte distorcida de lógica no Capítulo 3.
-
Sam Bull indicou um parágrafo confuso no Capítulo 2.
-
Andrew Cheung indicou duas ocorrências de “uso antes da definição”.
-
C. Corey Capel notou uma palavra ausente e um erro de ortografia no Capítulo 4.
-
Alessandra ajudou a eliminar algumas coisas confusas do Turtle.
-
Wim Champagne encontrou uma confusão de palavras em um exemplo de dicionário.
-
Douglas Wright indicou um problema com a divisão pelo piso em arc.
-
Jared Spindor encontrou uma confusão no fim de uma frase.
-
Lin Peiheng enviou várias sugestões muito úteis.
-
Ray Hagtvedt enviou dois erros e um quase erro.
-
Torsten Hübsch indicou uma inconsistência no Swampy.
-
Inga Petuhhov corrigiu um exemplo no Capítulo 14.
-
Arne Babenhauserheide enviou várias correções úteis.
-
Mark E. Casida é é bom em encontrar palavras repetidas.
-
Scott Tyler preencheu um que faltava. E em seguida enviou um monte de correções.
-
Gordon Shephard enviou várias correções, todas em emails separados.
-
Andrew Turner notou um erro no Capítulo 8.
-
Adam Hobart corrigiu um problema com a divisão pelo piso em arc.
-
Daryl Hammond e Sarah Zimmerman indicaram que eu trouxe o math.pi para a mesa cedo demais. E Zim achou um erro de ortografia.
-
George Sass encontrou um bug em uma seção de depuração.
-
Brian Bingham sugeriu o Exercício 11.5.
-
Leah Engelbert-Fenton indicou que usei tuple como um nome de variável, contrariando meu próprio conselho. E, em seguida, encontrou uma porção de erros de ortografia e um “uso antes da definição”.
-
Joe Funke achou um erro de ortografia.
-
Chao-chao Chen encontrou uma inconsistência no exemplo de Fibonacci.
-
Jeff Paine sabe a diferença entre espaço e spam.
-
Lubos Pintes enviou um erro de ortografia.
-
Gregg Lind e Abigail Heithoff sugeriram o Exercício 14.3.
-
Max Hailperin entregou uma série de correções e sugestões. Max é um dos autores das extraordinárias Abstrações Concretas (Tecnologia de curso, 1998), que você pode querer ler quando terminar este livro.
-
Chotipat Pornavalai encontrou um erro em uma mensagem de erro.
-
Stanislaw Antol enviou uma lista com várias sugestões úteis.
-
Eric Pashman enviou uma série de correções para os Capítulos 4-11.
-
Miguel Azevedo encontrou alguns erros de ortografia.
-
Jianhua Liu enviou uma longa lista de correções.
-
Nick King encontrou uma palavra que faltava.
-
Martin Zuther enviou uma longa lista de sugestões.
-
Adam Zimmerman encontrou uma inconsistência em uma ocorrência de “ocorrência” e vários outros erros.
-
Ratnakar Tiwari sugeriu uma nota de rodapé explicando triângulos degenerados.
-
Anurag Goel sugeriu outra solução para is_abecedarian e enviou algumas correções adicionais. E ele sabe soletrar Jane Austen.
-
Kelli Kratzer notou um dos erros de ortografia.
-
Mark Griffiths indicou um exemplo confuso no Capítulo 3.
-
Roydan Ongie encontrou um erro no meu método de Newton.
-
Patryk Wolowiec me ajudou com um problema na versão do HTML.
-
Mark Chonofsky me falou de uma nova palavra-chave no Python 3.
-
Russell Coleman ajudou com a minha geometria.
-
Wei Huang notou vários erros tipográficos.
-
Karen Barber achou o erro de ortografia mais antigo no livro.
-
Nam Nguyen encontrou um erro de ortografia e indicou que usei o Decorator, mas não mencionei o nome.
-
Stéphane Morin enviou várias correções e sugestões.
-
Paul Stoop corrigiu um erro de ortografia em uses_only.
-
Eric Bronner indicou uma confusão na discussão da ordem de operações.
-
Alexandros Gezerlis definiu um novo padrão para o número e a qualidade das sugestões que enviou. Estamos profundamente gratos!
-
Gray Thomas sabe diferenciar a direita da esquerda.
-
Giovanni Escobar Sosa enviou uma longa lista de correções e sugestões.
-
Alix Etienne corrigiu uma das URLs.
-
Kuang He encontrou um erro de ortografia.
-
Daniel Neilson corrigiu um erro sobre a ordem de operações.
-
Will McGinnis indicou que polyline foi definida de forma diferente em dois lugares.
-
Swarup Sahoo notou que faltava um ponto e vírgula.
-
Frank Hecker indicou que um exercício estava mal especificado e encontrou alguns links quebrados.
-
Animesh B me ajudou a esclarecer um exemplo confuso.
-
Martin Caspersen encontrou dois erros de arredondamento.
-
Gregor Ulm enviou várias correções e sugestões.
-
Dimitrios Tsirigkas sugeriu que eu esclarecesse um exercício.
-
Carlos Tafur enviou uma página de correções e sugestões.
-
Martin Nordsletten encontrou um bug na solução de um exercício.
-
Lars O.D. Christensen encontrou uma referência quebrada.
-
Vitor Simeone encontrou um erro de ortografia.
-
Sven Hoexter indicou que uma entrada de uma variável nomeada se sobrepõe a uma função integrada.
-
Viet Le encontrou um erro de ortografia.
-
Stephen Gregory indicou o problema com cmp no Python 3.
-
Matthew Shultz me avisou sobre um link quebrado.
-
Lokesh Kumar Makani me avisou sobre alguns links quebrados e algumas alterações em mensagens de erro.
-
Ishwar Bhat corrigiu minha declaração do último teorema de Fermat.
-
Brian McGhie sugeriu um esclarecimento.
-
Andrea Zanella traduziu o livro para o italiano e enviou uma série de correções ao longo do caminho.
-
Muito, muito obrigado a Melissa Lewis e Luciano Ramalho pelos comentários e sugestões excelentes na segunda edição.
-
Obrigado a Harry Percival do PythonAnywhere por ajudar as pessoas a começar a usar o Python em um navegador.
-
Xavier Van Aubel fez várias correções úteis na segunda edição.
Capítulo 1: A jornada do programa
O objetivo deste livro é ensinar a pensar como um cientista da computação. Esta forma de pensar combina algumas das melhores características da matemática, da engenharia e das ciências naturais. Assim como os matemáticos, os cientistas da computação usam linguagens formais para denotar ideias (especificamente operações de computação). Como engenheiros, eles projetam coisas, reunindo componentes em sistemas e avaliando as opções de melhor retorno entre as alternativas à disposição. Como cientistas, observam o comportamento de sistemas complexos, formam hipóteses e testam previsões.
A habilidade específica mais importante de um cientista da computação é a resolução de problemas. Resolução de problemas significa a capacidade de formular problemas, pensar criativamente em soluções e expressar uma solução de forma clara e precisa. Assim, o processo de aprender a programar é uma oportunidade excelente para exercitar a habilidade de resolver problemas. É por isso que este capítulo se chama “A jornada do programa”.
Em um nível você aprenderá a programar, uma habilidade útil por si mesma. Em outro nível usará a programação como um meio para um fim. Conforme avançarmos, este fim ficará mais claro.
1.1 - O que é um programa?
Um programa é uma sequência de instruções que especifica como executar uma operação de computação. A operação de computação pode ser algo matemático, como solucionar um sistema de equações ou encontrar as raízes de um polinômio, mas também pode ser uma operação de computação simbólica, como a busca e a substituição de textos em um documento; ou algo gráfico, como o processamento de uma imagem ou a reprodução de um vídeo.
Os detalhes parecem diferentes em linguagens diferentes, mas algumas instruções básicas aparecem em quase todas as linguagens:
entrada
Receber dados do teclado, de um arquivo, da rede ou de algum outro dispositivo.
saída
Exibir dados na tela, salvá-los em um arquivo, enviá-los pela rede etc.
matemática
Executar operações matemáticas básicas como adição e multiplicação.
execução condicional
Verificar a existência de certas condições e executar o código adequado.
repetição
Executar várias vezes alguma ação, normalmente com algumas variações.
Acredite ou não, isto é basicamente tudo o que é preciso saber. Cada programa que você já usou, complicado ou não, é composto de instruções muito parecidas com essas. Podemos então chegar à conclusão de que programar é o processo de quebrar uma tarefa grande e complexa em subtarefas cada vez menores, até que estas sejam simples o suficiente para serem executadas por uma dessas instruções básicas.
1.2 - Execução do Python
Um dos desafios de começar a usar Python é ter que instalar no seu computador o próprio programa e outros relacionados. Se tiver familiaridade com o seu sistema operacional, e especialmente se não tiver problemas com a interface de linha de comando, você não terá dificuldade para instalar o Python. Mas para principiantes pode ser trabalhoso aprender sobre administração de sistemas e programação ao mesmo tempo.
Para evitar esse problema, recomendo que comece a executar o Python em um navegador. Depois, quando você já conhecer o Python um pouco mais, darei sugestões para instalá-lo em seu computador.
Há uma série de sites que ajudam a usar e executar o Python. Se já tem um favorito, vá em frente e use-o. Senão, recomendo o PythonAnywhere. Apresento instruções detalhadas sobre os primeiros passos no link http://tinyurl.com/thinkpython2e.
Há duas versões do Python, o Python 2 e o Python 3. Como elas são muito semelhantes, se você aprender uma versão, é fácil trocar para a outra. Como é iniciante, você encontrará poucas diferenças. Este livro foi escrito para o Python 3, mas também incluí algumas notas sobre o Python 2.
O interpretador do Python é um programa que lê e executa o código Python. Dependendo do seu ambiente, é possível iniciar o interpretador clicando em um ícone, ou digitando python em uma linha de comando. Quando ele iniciar, você deverá ver uma saída como esta:
Python 3.4.0 (default, Jun 19 2015, 14:20:21)
[GCC 4.8.2] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>
As três primeiras linhas contêm informações sobre o interpretador e o sistema operacional em que está sendo executado, portanto podem ser diferentes para você. Mas é preciso conferir se o número da versão, que é 3.4.0 neste exemplo, começa com 3, o que indica que você está executando o Python 3. Se começar com 2, você está executando (adivinhe!) o Python 2.
A última linha é um prompt indicando que o interpretador está pronto para você digitar o código. Se digitar uma linha de código e pressionar Enter, o interpretador exibe o resultado:
>>> 1 + 1
2
Agora você está pronto para começar. Daqui em diante, vou supor que você sabe como inicializar o interpretador do Python e executar o código.
1.3 - O primeiro programa
Tradicionalmente, o primeiro programa que se escreve em uma nova linguagem chama-se “Hello, World!”, porque tudo o que faz é exibir as palavras “Hello, World!” na tela. No Python, ele se parece com isto:
>>> print('Hello, World!')
Este é um exemplo de uma instrução print (instrução de impressão), embora na realidade ela não imprima nada em papel. Ela exibe um resultado na tela. Nesse caso, o resultado são as palavras:
Hello, World!
As aspas apenas marcam o começo e o fim do texto a ser exibido; elas não aparecem no resultado.
Os parênteses indicam que o print é uma função. Veremos funções no Capítulo 3.
No Python 2, a instrução print é ligeiramente diferente; ela não é uma função, portanto não usa parênteses.
>>> print 'Hello, World!'
Esta distinção fará mais sentido em breve, mas isso é o suficiente para começar.
1.4 - Operadores aritméticos
Depois do “Hello, World”, o próximo passo é a aritmética. O Python tem operadores, que são símbolos especiais representando operações de computação, como adição e multiplicação.
Os operadores +, - e * executam a adição, a subtração e a multiplicação, como nos seguintes exemplos:
>>> 40 + 2
42
>>> 43 - 1
42
>>> 6 * 7
42
O operador / executa a divisão:
>>> 84 / 2
42.0
Pode ser que você fique intrigado pelo resultado ser 42.0 em vez de 42. Vou explicar isso na próxima seção.
Finalmente, o operador ** executa a exponenciação; isto é, eleva um número a uma potência:
>>> 6 ** 2 + 6
42
Em algumas outras linguagens, o ^ é usado para a exponenciação, mas no Python é um operador bitwise, chamado XOR. Se não tiver familiaridade com operadores bitwise, o resultado o surpreenderá:
>>> 6 ^ 2
4
Não abordarei operadores bitwise neste livro, mas você pode ler sobre eles em http://wiki.python.org/moin/BitwiseOperators.
1.5 - Valores e tipos
Um valor é uma das coisas básicas com as quais um programa trabalha, como uma letra ou um número. Alguns valores que vimos até agora foram 2, 42.0 e 'Hello, World!'.
Esses valores pertencem a tipos diferentes: 2 é um número inteiro, 42.0 é um número de ponto flutuante e 'Hello, World!' é uma string, assim chamada porque as letras que contém estão em uma sequência em cadeia.
Se não tiver certeza sobre qual é o tipo de certo valor, o interpretador pode dizer isso a você:
>>> type(2)
<class 'int'>
>>> type(42.0)
<class 'float'>
>>> type('Hello, World!')
<class 'str'>
Nesses resultados, a palavra “class” [classe] é usada no sentido de categoria; um tipo é uma categoria de valores.
Como se poderia esperar, números inteiros pertencem ao tipo int, strings pertencem ao tipo str e os números de ponto flutuante pertencem ao tipo float.
E valores como '2' e '42.0'? Parecem números, mas estão entre aspas como se fossem strings:
>>> type('2')
<class 'str'>
>>> type('42.0')
<class 'str'>
Então são strings.
Ao digitar um número inteiro grande, alguns podem usar a notação americana, com vírgulas entre grupos de dígitos, como em 1,000,000. Este não é um número inteiro legítimo no Python e resultará em:
>>> 1,000,000
(1, 0, 0)
O que não é de modo algum o que esperávamos! O Python interpreta 1,000,000 como uma sequência de números inteiros separados por vírgulas. Aprenderemos mais sobre este tipo de sequência mais adiante.
1.6 - Linguagens formais e naturais
As linguagens naturais são os idiomas que as pessoas falam, como inglês, espanhol e francês. Elas não foram criadas pelas pessoas (embora as pessoas tentem impor certa ordem a elas); desenvolveram-se naturalmente.
As linguagens formais são linguagens criadas pelas pessoas para aplicações específicas. Por exemplo, a notação que os matemáticos usam é uma linguagem formal especialmente boa para denotar relações entre números e símbolos. Os químicos usam uma linguagem formal para representar a estrutura química de moléculas. E o mais importante:
As linguagens de programação são idiomas formais criados para expressar operações de computação.
As linguagens formais geralmente têm regras de sintaxe estritas que governam a estrutura de declarações. Por exemplo, na matemática a declaração 3 + 3 = 6 tem uma sintaxe correta, mas não 3 + = 3$6. Na química, H2O é uma fórmula sintaticamente correta, mas 2Zz não é.
As regras de sintaxe vêm em duas categorias relativas a símbolos e estrutura. Os símbolos são os elementos básicos da linguagem, como palavras, números e elementos químicos. Um dos problemas com 3 + = 3$6 é que o $ não é um símbolo legítimo na matemática (pelo menos até onde eu sei). De forma similar, 2Zz não é legítimo porque não há nenhum elemento com a abreviatura Zz.
O segundo tipo de regra de sintaxe refere-se ao modo no qual os símbolos são combinados. A equação 3 + = 3 não é legítima porque, embora + e = sejam símbolos legítimos, não se pode ter um na sequência do outro. De forma similar, em uma fórmula química o subscrito vem depois do nome de elemento, não antes.
Esta é um@ frase bem estruturada em portuguê$, mas com s*mbolos inválidos. Esta frase todos os símbolos válidos tem, mas estrutura válida sem.
Ao ler uma frase em português ou uma declaração em uma linguagem formal, é preciso compreender a estrutura (embora em uma linguagem natural você faça isto de forma subconsciente). Este processo é chamado de análise.
Embora as linguagens formais e naturais tenham muitas características em comum – símbolos, estrutura e sintaxe – há algumas diferenças:
ambiguidade
As linguagens naturais são cheias de ambiguidade e as pessoas lidam com isso usando pistas contextuais e outras informações. As linguagens formais são criadas para ser quase ou completamente inequívocas, ou seja, qualquer afirmação tem exatamente um significado, independentemente do contexto.
redundância
Para compensar a ambiguidade e reduzir equívocos, as linguagens naturais usam muita redundância. Por causa disso, muitas vezes são verborrágicas. As linguagens formais são menos redundantes e mais concisas.
literalidade
As linguagens naturais são cheias de expressões e metáforas. Se eu digo “Caiu a ficha”, provavelmente não há ficha nenhuma na história, nem nada que tenha caído (esta é uma expressão para dizer que alguém entendeu algo depois de certo período de confusão). As linguagens formais têm significados exatamente iguais ao que expressam.
Como todos nós crescemos falando linguagens naturais, às vezes é difícil se ajustar a linguagens formais. A diferença entre a linguagem natural e a formal é semelhante à diferença entre poesia e prosa, mas vai além:
Poesia
As palavras são usadas tanto pelos sons como pelos significados, e o poema inteiro cria um efeito ou resposta emocional. A ambiguidade não é apenas comum, mas muitas vezes proposital.
Prosa
O significado literal das palavras é o mais importante e a estrutura contribui para este significado. A prosa é mais acessível à análise que a poesia, mas muitas vezes ainda é ambígua.
Programas
A significado de um programa de computador é inequívoco e literal e pode ser entendido inteiramente pela análise dos símbolos e da estrutura.
As linguagens formais são mais densas que as naturais, então exigem mais tempo para a leitura. Além disso, a estrutura é importante, então nem sempre é melhor ler de cima para baixo e da esquerda para a direita. Em vez disso, aprenda a analisar o programa primeiro, identificando os símbolos e interpretando a estrutura. E os detalhes fazem diferença. Pequenos erros em ortografia e pontuação, que podem não importar tanto nas linguagens naturais, podem fazer uma grande diferença em uma língua formal.
1.7 - Depuração
Os programadores erram. Por um capricho do destino, erros de programação são chamados de bugs (insetos) e o processo de rastreá-los chama-se depuração (debugging).
Programar, e especialmente fazer a depuração, às vezes traz emoções fortes. Se tiver dificuldade com certo bug, você pode ficar zangado, desesperado ou constrangido.
Há evidências de que as pessoas respondem naturalmente a computadores como se fossem pessoas. Quando funcionam bem, pensamos neles como parceiros da equipe, e quando são teimosos ou grosseiros, respondemos a eles do mesmo jeito que fazemos com pessoas grosseiras e teimosas (Reeves e Nass, The Media Equation: How People Treat Computers, Television, and New Media Like Real People and Places — A equação da mídia: como as pessoas tratam os computadores, a televisão e as novas mídias como se fossem pessoas e lugares reais).
Prepare-se para essas reações, pois isso pode ajudar a lidar com elas. Uma abordagem é pensar no computador como um funcionário com certas vantagens, como velocidade e precisão, e certas desvantagens, como a falta de empatia e a incapacidade de compreender um contexto mais amplo.
Seu trabalho é ser um bom gerente: encontrar formas de aproveitar as vantagens e atenuar as desvantagens. E também encontrar formas de usar suas emoções para lidar com o problema sem deixar suas reações interferirem na sua capacidade de trabalho.
Aprender a depurar erros pode ser frustrante, mas é uma habilidade valiosa, útil para muitas atividades além da programação. No fim de cada capítulo há uma seção como esta, com as minhas sugestões para fazer a depuração. Espero que sejam úteis!
1.8 - Glossário
resolução de problemas
O processo de formular um problema, encontrar uma solução e expressá-la.
linguagem de alto nível
Uma linguagem de programação como Python, que foi criada com o intuito de ser fácil para os humanos escreverem e lerem.
linguagem de baixo nível
Uma linguagem de programação criada para o computador executar com facilidade; também chamada de “linguagem de máquina” ou “linguagem assembly”.
portabilidade
A propriedade de um programa de poder ser executado em mais de um tipo de computador.
interpretador
Um programa que lê outro programa e o executa.
prompt
Caracteres expostos pelo interpretador para indicar que está pronto para receber entradas do usuário.
programa
Conjunto de instruções que especificam uma operação de computação.
instrução print
Uma instrução que faz o interpretador do Python exibir um valor na tela.
operador
Um símbolo especial que representa uma operação de computação simples como adição, multiplicação ou concatenação de strings.
valor
Uma das unidades básicas de dados, como um número ou string, que um programa manipula.
tipo
Uma categoria de valores. Os tipos que vimos por enquanto são números inteiros (tipo int), números de ponto flutuante (tipo float) e strings (tipo str).
inteiro
Um tipo que representa números inteiros.
ponto flutuante
Um tipo que representa números com partes fracionárias.
string
Um tipo que representa sequências de caracteres.
linguagem natural
Qualquer linguagem que as pessoas falam e que se desenvolveu naturalmente.
linguagem formal
Qualquer linguagem que as pessoas criaram com objetivos específicos, como representar ideias matemáticas ou programas de computador; todas as linguagens de programação são linguagens formais.
símbolo
Um dos elementos básicos da estrutura sintática de um programa, análogo a uma palavra em linguagem natural.
sintaxe
As regras que governam a estrutura de um programa.
análise
Examinar um programa e sua estrutura sintática.
bug
Um erro em um programa.
depuração
O processo de encontrar e corrigir (depurar) bugs.
1.9 - Exercícios
Exercício 1.1
É uma boa ideia ler este livro em frente a um computador para testar os exemplos durante a leitura.
Sempre que estiver testando um novo recurso, você deve tentar fazer erros. Por exemplo, no programa “Hello, World!”, o que acontece se omitir uma das aspas? E se omitir ambas? E se você soletrar a instrução print de forma errada?
Este tipo de experimento ajuda a lembrar o que foi lido; também ajuda quando você estiver programando, porque assim conhecerá o significado das mensagens de erro. É melhor fazer erros agora e de propósito que depois e acidentalmente.
-
Em uma instrução print, o que acontece se você omitir um dos parênteses ou ambos?
-
Se estiver tentando imprimir uma string, o que acontece se omitir uma das aspas ou ambas?
-
Você pode usar um sinal de menos para fazer um número negativo como -2. O que acontece se puser um sinal de mais antes de um número? E se escrever assim: 2++2?
-
Na notação matemática, zeros à esquerda são aceitáveis, como em 02. O que acontece se você tentar usar isso no Python?
-
O que acontece se você tiver dois valores sem nenhum operador entre eles?
Exercício 1.2
Inicialize o interpretador do Python e use-o como uma calculadora.
-
Quantos segundos há em 42 minutos e 42 segundos?
-
Quantas milhas há em 10 quilômetros? Dica: uma milha equivale a 1,61 quilômetro.
-
Se você correr 10 quilômetros em 42 minutos e 42 segundos, qual é o seu passo médio (tempo por milha em minutos e segundos)? Qual é a sua velocidade média em milhas por hora?
Capítulo 2: Variáveis, expressões e instruções
Um dos recursos mais eficientes de uma linguagem de programação é a capacidade de manipular variáveis. Uma variável é um nome que se refere a um valor.
2.1 - Instruções de atribuição
Uma instrução de atribuição cria uma nova variável e dá um valor a ela:
>>> message = 'And now for something completely different'
>>> n = 17
>>> pi = 3.141592653589793
Esse exemplo faz três atribuições. A primeira atribui uma string a uma nova variável chamada message; a segunda dá o número inteiro 17 a n; a terceira atribui o valor (aproximado) de π a pi.
Uma forma comum de representar variáveis por escrito é colocar o nome com uma flecha apontando para o seu valor. Este tipo de número é chamado de diagrama de estado porque mostra o estado no qual cada uma das variáveis está (pense nele como o estado de espírito da variável). A Figura 2.1 mostra o resultado do exemplo anterior.
 .
.
Figura 2.1 – Diagrama de estado.
2.2 - Nomes de variáveis
Os programadores geralmente escolhem nomes significativos para as suas variáveis – eles documentam o uso da variável.
Nomes de variáveis podem ser tão longos quanto você queira. Podem conter tanto letras como números, mas não podem começar com um número. É legal usar letras maiúsculas, mas a convenção é usar apenas letras minúsculas para nomes de variáveis.
O caractere de sublinhar (_) pode aparecer em um nome. Muitas vezes é usado em nomes com várias palavras, como your_name ou airspeed_of_unladen_swallow.
Se você der um nome ilegal a uma variável, recebe um erro de sintaxe:
>>> 76trombones = 'big parade'
SyntaxError: invalid syntax
>>> more@ = 1000000
SyntaxError: invalid syntax
>>> class = 'Advanced Theoretical Zymurgy'
SyntaxError: invalid syntax
76trombones é ilegal porque começa com um número. more@ é ilegal porque contém um caractere ilegal, o @. Mas o que há de errado com class?
A questão é que class é uma das palavras-chave do Python. O interpretador usa palavras-chave para reconhecer a estrutura do programa e elas não podem ser usadas como nomes de variável.
O Python 3 tem estas palavras-chave:
and del from None True
as elif global nonlocal try
assert else if not while
break except import or with
class False in pass yield
continue finally is raise
def for lambda return
Você não precisa memorizar essa lista. Na maior parte dos ambientes de desenvolvimento, as palavras-chave são exibidas em uma cor diferente; se você tentar usar uma como nome de variável, vai perceber.
2.3 - Expressões e instruções
Uma expressão é uma combinação de valores, variáveis e operadores. Um valor por si mesmo é considerado uma expressão, assim como uma variável, portanto as expressões seguintes são todas legais:
>>> 42
42
>>> n
17
>>> n + 25
42
Quando você digita uma expressão no prompt, o interpretador a avalia, ou seja, ele encontra o valor da expressão. Neste exemplo, o n tem o valor 17 e n + 25 tem o valor 42.
Uma instrução é uma unidade de código que tem um efeito, como criar uma variável ou exibir um valor.
>>> n = 17
>>> print(n)
A primeira linha é uma instrução de atribuição que dá um valor a n. A segunda linha é uma instrução de exibição que exibe o valor de n.
Quando você digita uma instrução, o interpretador a executa, o que significa que ele faz o que a instrução diz. Em geral, instruções não têm valores.
2.4 - Modo script
Até agora executamos o Python no modo interativo, no qual você interage diretamente com o interpretador. O modo interativo é uma boa forma de começar, mas se estiver trabalhando com mais do que algumas linhas do código, o processo pode ficar desorganizado.
A alternativa é salvar o código em um arquivo chamado script e então executar o interpretador no modo script para executá-lo. Por convenção, os scripts no Python têm nomes que terminam com .py.
Se souber como criar e executar um script no seu computador, você está pronto. Senão, recomendo usar o PythonAnywhere novamente. Inseri instruções sobre como executar programas no modo script em http://tinyurl.com/thinkpython2e.
Como o Python oferece os dois modos, você pode testar pedaços do código no modo interativo antes de colocá-los em um script. Mas há diferenças entre o modo interativo e o modo script que podem confundir as pessoas.
Por exemplo, se estiver usando o Python como uma calculadora, você poderia digitar:
>>> miles = 26.2
>>> miles * 1.61
42.182
A primeira linha atribui um valor a miles, mas não tem efeito visível. A segunda linha é uma expressão, então o interpretador a avalia e exibe o resultado. No fim, chega-se ao resultado de que uma maratona tem aproximadamente 42 quilômetros.
Mas se você digitar o mesmo código em um script e executá-lo, não recebe nenhuma saída. Uma expressão, por conta própria, não tem efeito visível no modo script. O Python, na verdade, avalia a expressão, mas não exibe o valor a menos que você especifique:
miles = 26.2
print(miles * 1.61)
Este comportamento pode confundir um pouco no início.
Um script normalmente contém uma sequência de instruções. Se houver mais de uma instrução, os resultados aparecem um após o outro, conforme as instruções sejam executadas.
Por exemplo, o script
print(1)
x = 2
print(x)
produz a saída
1
2
A instrução de atribuição não produz nenhuma saída.
Para verificar sua compreensão, digite as seguintes instruções no interpretador do Python e veja o que fazem:
5
x = 5
x + 1
Agora ponha as mesmas instruções em um script e o execute. Qual é a saída? Altere o script transformando cada expressão em uma instrução de exibição e então o execute novamente.
2.5 - Ordem das operações
Quando uma expressão contém mais de um operador, a ordem da avaliação depende da ordem das operações. Para operadores matemáticos, o Python segue a convenção matemática. O acrônimo PEMDAS pode ser útil para lembrar das regras:
-
Os Parênteses têm a precedência mais alta e podem ser usados para forçar a avaliação de uma expressão na ordem que você quiser. Como as expressões em parênteses são avaliadas primeiro,
2 * (3-1)é 4, e(1+1)**(5-2)é 8. Também é possível usar parênteses para facilitar a leitura de uma expressão, como no caso de(minute * 100) / 60, mesmo se o resultado não for alterado. -
A Exponenciação tem a próxima precedência mais alta, então
1 + 2**3é 9, não 27, e2 * 3**2é 18, não 36. -
A Multiplicação e a Divisão têm precedência mais alta que a Adição e a Subtração. Assim,
2 * 3 - 1é 5, não 4, e6 + 4 / 2é 8, não 5. -
Os operadores com a mesma precedência são avaliados da esquerda para a direita (exceto na exponenciação). Assim, na expressão
degrees / 2 * pi, a divisão acontece primeiro e o resultado é multiplicado porpi. Para dividir por 2π, você pode usar parênteses ou escreverdegrees / 2 / pi.
Eu não fico sempre tentando lembrar da precedência de operadores. Se a expressão não estiver clara à primeira vista, uso parênteses para fazer isso.
2.6 - Operações com strings
Em geral, não é possível executar operações matemáticas com strings, mesmo se elas parecerem números, então coisas assim são ilegais:
'2'-'1' 'eggs'/'easy' 'third'*'a charm'
Mas há duas exceções, + e *.
O operador + executa uma concatenação de strings, ou seja, une as strings pelas extremidades. Por exemplo:
>>> first = 'throat'
>>> second = 'warbler'
>>> first + second
throatwarbler
O operador * também funciona em strings; ele executa a repetição. Por exemplo, 'Spam'*3 é 'SpamSpamSpam'. Se um dos valores for uma string, o outro tem de ser um número inteiro.
Este uso de + e * faz sentido por analogia com a adição e a multiplicação. Tal como 4 * 3 é equivalente a 4 + 4 + 4, esperamos que 'Spam' * 3 seja o mesmo que 'Spam'+'Spam'+'Spam', e assim é. Por outro lado, há uma diferença significativa entre a concatenação de strings e a repetição em relação à adição e à multiplicação de números inteiros. Você consegue pensar em uma propriedade que a adição tem, mas a concatenação de strings não tem?
2.7 - Comentários
Conforme os programas ficam maiores e mais complicados, eles são mais difíceis de ler. As linguagens formais são densas e muitas vezes é difícil ver um pedaço de código e compreender o que ele faz ou por que faz isso.
Por essa razão, é uma boa ideia acrescentar notas aos seus programas para explicar em linguagem natural o que o programa está fazendo. Essas notas são chamadas de comentários, e começam com o símbolo #:
# computa a percentagem da hora que passou
percentage = (minute * 100) / 60
Nesse caso, o comentário aparece sozinho em uma linha. Você também pode pôr comentários no fim das linhas:
percentage = (minute * 100) / 60 # percentagem de uma hora
Tudo do # ao fim da linha é ignorado – não tem efeito na execução do programa.
Os comentários tornam-se mais úteis quando documentam algo no código que não está óbvio. Podemos supor que o leitor compreenda o que o código faz; assim, é mais útil explicar porque faz o que faz.
Este comentário é redundante em relação ao código, além de inútil:
v = 5 # atribui 5 a v
Este comentário contém informações úteis que não estão no código:
v = 5 # velocidade em metros/segundo.
Bons nomes de variáveis podem reduzir a necessidade de comentários, mas nomes longos podem tornar expressões complexas difíceis de ler, então é preciso analisar o que vale mais a pena.
2.8 - Depuração
Há três tipos de erros que podem ocorrer em um programa: erros de sintaxe, erros de tempo de execução e erros semânticos. É útil distinguir entre eles para rastreá-los mais rapidamente.
Erro de sintaxe
A “sintaxe” refere-se à estrutura de um programa e suas respectivas regras. Por exemplo, os parênteses devem vir em pares correspondentes, então (1 + 2) é legal, mas 8) é um erro de sintaxe. Se houver um erro de sintaxe em algum lugar no seu programa, o Python exibe uma mensagem de erro e para, e não será possível executar o programa. Nas primeiras poucas semanas da sua carreira em programação, você pode passar muito tempo rastreando erros de sintaxe. Ao adquirir experiência, você fará menos erros e os encontrará mais rápido.
Erro de tempo de execução
O segundo tipo de erro é o erro de tempo de execução, assim chamado porque o erro não aparece até que o programa seja executado. Esses erros também se chamam de exceções porque normalmente indicam que algo excepcional (e ruim) aconteceu. Os erros de tempo de execução são raros nos programas simples que veremos nos primeiros capítulos, então pode demorar um pouco até você encontrar algum.
Erro semântico
O terceiro tipo do erro é “semântico”, ou seja, relacionado ao significado. Se houver um erro semântico no seu programa, ele será executado sem gerar mensagens de erro, mas não vai fazer a coisa certa. Vai fazer algo diferente. Especificamente, vai fazer o que você disser para fazer. Identificar erros semânticos pode ser complicado, porque é preciso trabalhar de trás para a frente, vendo a saída do programa e tentando compreender o que ele está fazendo.
2.9 - Glossário
variável
Um nome que se refere a um valor.
atribuição
Uma instrução que atribui um valor a uma variável.
diagrama de estado
Uma representação gráfica de um grupo de variáveis e os valores a que se referem.
palavra-chave
Uma palavra reservada, usada para analisar um programa; não é possível usar palavras-chave como if, def e while como nomes de variáveis.
operando
Um dos valores que um operador produz.
expressão
Uma combinação de variáveis, operadores e valores que representa um resultado único.
avaliar
Simplificar uma expressão executando as operações para produzir um valor único.
instrução
Uma seção do código que representa um comando ou ação. Por enquanto, as instruções que vimos são instruções de atribuições e de exibição.
executar
Executar uma instrução para fazer o que ela diz.
modo interativo
Um modo de usar o interpretador do Python, digitando o código no prompt.
modo script
Um modo de usar o interpretador do Python para ler código em um script e executá-lo.
script
Um programa armazenado em um arquivo.
ordem das operações
As regras que governam a ordem na qual as expressões que envolvem vários operadores e operandos são avaliadas.
concatenar
Juntar dois operandos pelas extremidades.
comentários
Informações em um programa destinadas a outros programadores (ou qualquer pessoa que leia o texto fonte) que não têm efeito sobre a execução do programa.
erro de sintaxe
Um erro em um programa que torna sua análise impossível (e por isso impossível de interpretar).
exceção
Um erro que se descobre quando o programa é executado.
semântica
O significado de um programa.
erro semântico
Um erro que faz com que um programa faça algo diferente do que o programador pretendia.
2.10 - Exercícios
Exercício 2.1
Repetindo o meu conselho do capítulo anterior, sempre que você aprender um recurso novo, você deve testá-lo no modo interativo e fazer erros de propósito para ver o que acontece.
-
Vimos que n = 42 é legal. E 42 = n?
-
Ou x = y = 1?
-
Em algumas linguagens, cada instrução termina em um ponto e vírgula ;. O que acontece se você puser um ponto e vírgula no fim de uma instrução no Python?
-
E se puser um ponto no fim de uma instrução?
-
Em notação matemática é possível multiplicar x e y desta forma: xy. O que acontece se você tentar fazer o mesmo no Python?
Exercício 2.2
Pratique o uso do interpretador do Python como uma calculadora:
-
O volume de uma esfera com raio r é
 .. Qual é o volume de uma esfera com raio 5?
.. Qual é o volume de uma esfera com raio 5? -
Suponha que o preço de capa de um livro seja R$ 24,95, mas as livrarias recebem um desconto de 40%. O transporte custa R$ 3,00 para o primeiro exemplar e 75 centavos para cada exemplar adicional. Qual é o custo total de atacado para 60 cópias?
-
Se eu sair da minha casa às 6:52 e correr 1 quilômetro a um certo passo (8min15s por quilômetro), então 3 quilômetros a um passo mais rápido (7min12s por quilômetro) e 1 quilômetro no mesmo passo usado em primeiro lugar, que horas chego em casa para o café da manhã?
Capítulo 3: Funções
No contexto da programação, uma função é uma sequência nomeada de instruções que executa uma operação de computação. Ao definir uma função, você especifica o nome e a sequência de instruções. Depois, pode “chamar” a função pelo nome.
3.1 - Chamada de função
Já vimos um exemplo de chamada de função:
>>> type(42)
<class 'int'>
O nome da função é type. A expressão entre parênteses é chamada de argumento da função. Para esta função, o resultado é o tipo do argumento.
É comum dizer que uma função “recebe” um argumento e “retorna” um resultado. O resultado também é chamado de valor de retorno.
O Python oferece funções que convertem valores de um tipo em outro. A função int recebe qualquer valor e o converte em um número inteiro, se for possível, ou declara que há um erro:
>>> int('32')
32
>>> int('Hello')
ValueError: invalid literal for int(): Hello
int pode converter valores de ponto flutuante em números inteiros, mas não faz arredondamentos; ela apenas corta a parte da fração:
>>> int(3.99999)
3
>>> int(-2.3)
-2
float converte números inteiros e strings em números de ponto flutuante:
>>> float(32)
32.0
>>> float('3.14159')
3.14159
Finalmente, str converte o argumento em uma string:
>>> str(32)
'32'
>>> str(3.14159)
'3.14159'
3.2 - Funções matemáticas
O Python tem um módulo matemático que oferece a maioria das funções matemáticas comuns. Um módulo é um arquivo que contém uma coleção de funções relacionadas.
Antes que possamos usar as funções em um módulo, precisamos importá-lo com uma instrução de importação:
>>> import math
Esta instrução cria um objeto de módulo chamado math (matemática). Ao se exibir o objeto de módulo, são apresentadas informações sobre ele:
>>> math
<module 'math' (built-in)>
O objeto de módulo contém as funções e variáveis definidas no módulo. Para acessar uma das funções, é preciso especificar o nome do módulo e o nome da função, separados por um ponto. Este formato é chamado de notação de ponto.
>>> ratio = signal_power / noise_power
>>> decibels = 10 * math.log10(ratio)
>>> radians = 0.7
>>> height = math.sin(radians)
O primeiro exemplo usa math.log10 para calcular a proporção de sinal e de ruído em decibéis (assumindo que signal_power e noise_power tenham sido definidos). O módulo matemático também oferece a função log, que calcula logaritmos de base e.
O segundo exemplo encontra o seno de radians. O nome da variável indica que sin e outras funções trigonométricas (cos, tan etc) recebem argumentos em radianos. Para converter graus em radianos, divida por 180 e multiplique por π:
>>> degrees = 45
>>> radians = degrees / 180.0 * math.pi
>>> math.sin(radians)
0.707106781187
A expressão math.pi recebe a variável pi do módulo matemático. Seu valor é uma aproximação de ponto flutuante de π, com precisão aproximada de 15 dígitos.
Se souber trigonometria, você pode verificar o resultado anterior comparando-o com a raiz quadrada de 2 dividida por 2:
>>> math.sqrt(2) / 2.0
0.707106781187
3.3 - Composição
Por enquanto, falamos sobre os elementos de um programa – variáveis, expressões e instruções – de forma isolada, mas não sobre como combiná-los.
Uma das características mais úteis das linguagens de programação é a sua capacidade de usar pequenos blocos de montar para compor programas. Por exemplo, o argumento de uma função pode ser qualquer tipo de expressão, inclusive operadores aritméticos:
x = math.sin(degrees / 360.0 * 2 * math.pi)
E até chamadas de função:
x = math.exp(math.log(x+1))
É possível colocar um valor, uma expressão arbitrária, em quase qualquer lugar. Com uma exceção: o lado esquerdo de uma instrução de atribuição tem que ser um nome de variável. Qualquer outra expressão no lado esquerdo é um erro de sintaxe (veremos exceções a esta regra depois).
>>> minutes = hours * 60 # correto
>>> hours * 60 = minutes # errado!
SyntaxError: can't assign to operator
3.4 - Como acrescentar novas funções
Por enquanto, só usamos funções que vêm com o Python, mas também é possível acrescentar novas funções. Uma definição de função especifica o nome de uma nova função e a sequência de instruções que são executadas quando a função é chamada.
Aqui está um exemplo:
def print_lyrics():
print("I'm a lumberjack, and I'm okay.")
print("I sleep all night and I work all day.")
def é uma palavra-chave que indica uma definição de função. O nome da função é print_lyrics. As regras para nomes de função são as mesmas que as das variáveis: letras, números e sublinhado são legais, mas o primeiro caractere não pode ser um número. Não podemos usar uma palavra-chave como nome de uma função e devemos evitar ter uma variável e uma função com o mesmo nome.
Os parênteses vazios depois do nome indicam que esta função não usa argumentos.
A primeira linha da definição de função chama-se cabeçalho; o resto é chamado de corpo. O cabeçalho precisa terminar em dois pontos e o corpo precisa ser endentado. Por convenção, a endentação sempre é de quatro espaços. O corpo pode conter qualquer número de instruções.
As strings nas instruções de exibição são limitadas por aspas duplas. As aspas simples e as aspas duplas fazem a mesma coisa; a maior parte das pessoas usa aspas simples apenas nos casos em que aspas simples (que também são apóstrofes) aparecem na string.
Todas as aspas (simples e duplas) devem ser “aspas retas”, normalmente encontradas ao lado do Enter no teclado. “Aspas curvas”, como as desta oração, não são legais no Python.
Se digitar uma definição de função no modo interativo, o interpretador exibe pontos (..) para mostrar que a definição não está completa:
>>> def print_lyrics():
... print("I'm a lumberjack, and I'm okay.")
... print("I sleep all night and I work all day.")
...
Para terminar a função, é preciso inserir uma linha vazia.
A definição de uma função cria um objeto de função, que tem o tipo function:
>>> print(print_lyrics)
<function print_lyrics at 0xb7e99e9c>
>>> type(print_lyrics)
<class 'function'>
A sintaxe para chamar a nova função é a mesma que a das funções integradas:
>>> print_lyrics()
I'm a lumberjack, and I'm okay.
I sleep all night and I work all day.
Uma vez que a função tenha sido definida, é possível usá-la dentro de outra função. Por exemplo, para repetir o refrão anterior, podemos escrever uma função chamada repeat_lyrics:
def repeat_lyrics():
print_lyrics()
print_lyrics()
E daí chamar repeat_lyrics:
>>> repeat_lyrics()
I'm a lumberjack, and I'm okay.
I sleep all night and I work all day.
I'm a lumberjack, and I'm okay.
I sleep all night and I work all day.
Mas a canção não é bem assim.
3.5 - Uso e definições
Juntando fragmentos de código da seção anterior, o programa inteiro fica assim:
def print_lyrics():
print("I'm a lumberjack, and I'm okay.")
print("I sleep all night and I work all day.")
def repeat_lyrics():
print_lyrics()
print_lyrics()
repeat_lyrics()
Este programa contém duas definições de função: print_lyrics e repeat_lyrics. As definições de função são executadas como outras instruções, mas o efeito é criar objetos de função. As instruções dentro da função não são executadas até que a função seja chamada, e a definição de função não gera nenhuma saída.
Como poderíamos esperar, é preciso criar uma função antes de executá-la. Em outras palavras, a definição de função tem que ser executada antes que a função seja chamada.
Como exercício, mova a última linha deste programa para o topo, para que a chamada de função apareça antes das definições. Execute o programa e veja qual é a mensagem de erro que aparece.
Agora mova a chamada de função de volta para baixo e mova a definição de print_lyrics para depois da definição de repeat_lyrics. O que acontece quando este programa é executado?
3.6 - Fluxo de execução
Para garantir que uma função seja definida antes do seu primeiro uso, é preciso saber a ordem na qual as instruções serão executadas. Isso é chamado de fluxo de execução.
A execução sempre começa na primeira instrução do programa. As instruções são executadas uma após a outra, de cima para baixo.
As definições de função não alteram o fluxo da execução do programa, mas lembre-se de que as instruções dentro da função não são executadas até a função ser chamada.
Uma chamada de função é como um desvio no fluxo de execução. Em vez de ir à próxima instrução, o fluxo salta para o corpo da função, executa as instruções lá, e então volta para continuar de onde parou.
Parece bastante simples, até você lembrar que uma função pode chamar outra. Enquanto estiver no meio de uma função, o programa pode ter que executar as instruções em outra função. Então, enquanto estiver executando a nova função, o programa pode ter que executar mais uma função!
Felizmente, o Python é bom em não perder o fio da meada, então cada vez que uma função é concluída, o programa continua de onde parou na função que o chamou. Quando chega no fim do programa, ele é encerrado.
Resumindo, nem sempre se deve ler um programa de cima para baixo. Às vezes faz mais sentido seguir o fluxo de execução.
3.7 - Parâmetros e argumentos
Algumas funções que vimos exigem argumentos. Por exemplo, ao chamar math.sin, você usa um número como argumento. Algumas funções exigem mais de um argumento: o math.pow exige dois, a base e o expoente.
Dentro da função, os argumentos são atribuídos a variáveis chamadas parâmetros. Aqui está a definição de uma função que precisa de um argumento:
def print_twice(bruce):
print(bruce)
print(bruce)
Esta função atribui o argumento a um parâmetro chamado bruce. Quando a função é chamada, ela exibe o valor do parâmetro (seja qual for) duas vezes.
Esta função funciona com qualquer valor que possa ser exibido:
>>> print_twice('Spam')
Spam
Spam
>>> print_twice(42)
42
42
>>> print_twice(math.pi)
3.14159265359
3.14159265359
As mesmas regras de composição usadas para funções integradas também são aplicadas a funções definidas pelos programadores, então podemos usar qualquer tipo de expressão como argumento para print_twice:
>>> print_twice('Spam '*4)
Spam Spam Spam Spam
Spam Spam Spam Spam
>>> print_twice(math.cos(math.pi))
-1.0
-1.0
O argumento é avaliado antes de a função ser chamada. Então, nos exemplos, as expressões 'Spam * 4 e math.cos(math.pi) só são avaliadas uma vez.
Você também pode usar uma variável como argumento:
>>> michael = 'Eric, the half a bee.'
>>> print_twice(michael)
Eric, the half a bee.
Eric, the half a bee.
O nome da variável que passamos como argumento (michael) não tem nada a ver com o nome do parâmetro (bruce). Não importa que o valor tenha sido chamado de volta (em quem chama); aqui em print_twice, chamamos todo mundo de bruce.
3.8 - As variáveis e os parâmetros são locais
Quando você cria uma variável dentro de uma função, ela é local, ou seja, ela só existe dentro da função. Por exemplo:
def cat_twice(part1, part2):
cat = part1 + part2
print_twice(cat)
Esta função recebe dois argumentos, concatena-os e exibe o resultado duas vezes. Aqui está um exemplo que a usa:
>>> line1 = 'Bing tiddle '
>>> line2 = 'tiddle bang.'
>>> cat_twice(line1, line2)
Bing tiddle tiddle bang.
Bing tiddle tiddle bang.
Quando cat_twice é encerrada, a variável cat é destruída. Se tentarmos exibi-la, recebemos uma exceção:
>>> print(cat)
NameError: name 'cat' is not defined
Os parâmetros também são locais. Por exemplo, além de print_twice, não existe o bruce.
3.9 - Diagrama da pilha
Para monitorar quais variáveis podem ser usadas e onde, é uma boa ideia desenhar um diagrama da pilha. Assim como diagramas de estado, os diagramas da pilha mostram o valor de cada variável, mas também mostram a função à qual cada variável pertence.
Cada função é representada por um frame (quadro). Um frame é uma caixa com o nome de uma função junto a ele e os parâmetros e as variáveis da função dentro dele. O diagrama da pilha para o exemplo anterior é exibido na Figura 3.1.
 .
.
Figura 3.1 – Diagrama da pilha.
Os frames são organizados em uma pilha que indica qual função que foi chamada por outra, e assim por diante. Neste exemplo, print_twice foi chamada por cat_twice e cat_twice foi chamada por __main__, que é um nome especial para o frame na posição mais proeminente. Quando você cria uma variável fora de qualquer função, ela pertence a __main__.
Cada parâmetro refere-se ao mesmo valor como seu argumento correspondente. Desta forma, part1 tem o mesmo valor que line1, part2 tem o mesmo valor que line2 e bruce tem o mesmo valor que cat.
Se ocorrer um erro durante uma chamada de função, o Python exibe o nome da função, o nome da função que a chamou e o nome da função que chamou esta função por sua vez, voltando até __main__.
Por exemplo, se você tentar acessar cat de dentro de print_twice, receberá uma mensagem de NameError:
Traceback (innermost last):
File "test.py", line 13, in __main__
cat_twice(line1, line2)
File "test.py", line 5, in cat_twice
print_twice(cat)
File "test.py", line 9, in print_twice
print(cat)
NameError: name 'cat' is not defined
Esta lista de funções é chamada de traceback. Ela mostra o arquivo do programa em que o erro ocorreu e em que linha, e quais funções estavam sendo executadas no momento. Ele também mostra a linha de código que causou o erro.
A ordem das funções no traceback é a mesma que a ordem dos frames no diagrama da pilha. A função que está sendo executada no momento está no final.
3.10 - Funções com resultado e funções nulas
Algumas funções que usamos, como as funções matemáticas, devolvem resultados; por falta de um nome melhor, vou chamá-las de funções com resultados. Outras funções, como print_twice, executam uma ação, mas não devolvem um valor. Elas são chamadas de funções nulas.
Quando você chama uma função com resultado, quase sempre quer fazer algo com o resultado; por exemplo, você pode atribui-lo a uma variável ou usá-la como parte de uma expressão:
x = math.cos(radians)
golden = (math.sqrt(5) + 1) / 2
Quando você chama uma função no modo interativo, o Python exibe o resultado:
>>> math.sqrt(5)
2.2360679774997898
Mas em um script, se você chamar uma função com resultado e mais nada, o valor de retorno é perdido para sempre!
math.sqrt(5)
Este script calcula a raiz quadrada de 5, mas como não armazena ou exibe o resultado, não é muito útil.
As funções nulas podem exibir algo na tela ou ter algum outro efeito, mas não têm um valor de retorno. Se você atribuir o resultado a uma variável, recebe um valor especial chamado None:
>>> result = print_twice('Bing')
Bing
Bing
>>> print(result)
None
O valor None não é o mesmo que a string 'None'. É um valor especial que tem seu próprio tipo:
>>> print(type(None))
<class 'NoneType'>
As funções que apresentamos por enquanto são todas nulas. Vamos apresentar funções com resultado mais adiante.
3.11 - Por que funções?
Caso o objetivo de dividir um programa em funções não esteja claro, saiba que na verdade há várias razões:
-
Criar uma nova função dá a oportunidade de nomear um grupo de instruções, o que deixa o seu programa mais fácil de ler e de depurar.
-
As funções podem tornar um programa menor, eliminando o código repetitivo. Depois, se fizer alguma alteração, basta fazê-la em um lugar só.
-
Dividir um programa longo em funções permite depurar as partes uma de cada vez e então reuni-las em um conjunto funcional.
-
As funções bem projetadas muitas vezes são úteis para muitos programas. Uma vez que escreva e depure uma, você pode reutilizá-la.
3.12 - Depuração
Uma das habilidades mais importantes que você vai aprender é a depuração. Embora possa ser frustrante, a depuração é uma das partes mais intelectualmente ricas, desafiadoras e interessantes da programação.
De certa forma, depurar é similar ao trabalho de um detetive. Você tem pistas e precisa inferir os processos e eventos que levaram aos resultados exibidos.
A depuração também é como ciência experimental. Uma vez que você tenha uma ideia sobre o que está errado, basta alterar o programa e tentar novamente. Se a sua hipótese estava correta, você pode prever o resultado da alteração e chegar um passo mais perto de um programa funcional. Se a sua hipótese estava errada, é preciso criar outra. Como dizia Sherlock Holmes, “Quando se elimina o impossível, o que sobra, por mais incrível que pareça, só pode ser a verdade.” (A. Conan Doyle, O signo dos quatro).
Para algumas pessoas, programar e depurar são a mesma coisa. Isto é, a programação é o processo de depurar gradualmente um programa até que ele faça o que o programador quer. A ideia é que você comece com um programa funcional e faça pequenas alterações, depurando-as no decorrer do trabalho.
Por exemplo, o Linux é um sistema operacional que contém milhões de linhas de código, mas começou como um programa simples que Linus Torvalds usava para explorar o chip Intel 80386. Segundo Larry Greenfield, “Um dos primeiros projetos de Linus foi um programa que alternaria entre a exibição de AAAA e BBBB. Mais tarde isso se desenvolveu até virar o Linux.” (Guia do usuário de Linux versão beta 1).
3.13 - Glossário
função
Uma sequência nomeada de declarações que executa alguma operação útil. As funções podem receber argumentos ou não e podem ou não produzir algum resultado.
definição de função
Uma instrução que cria uma função nova, especificando seu nome, parâmetros e as instruções que contém.
objeto da função
Um valor é criado por uma definição de função. O nome da função é uma variável que se refere a um objeto de função.
cabeçalho
A primeira linha de uma definição de função.
corpo
A sequência de instruções dentro de uma definição de função.
parâmetro
Um nome usado dentro de uma função para se referir ao valor passado como argumento.
chamada de função
Uma instrução que executa uma função. É composta pelo nome da função seguido de uma lista de argumentos entre parênteses.
argumento
Um valor apresentado a uma função quando a função é chamada. Este valor é atribuído ao parâmetro correspondente na função.
variável local
Uma variável definida dentro de uma função. Uma variável local só pode ser usada dentro da sua função.
valor de retorno
O resultado de uma função. Se uma chamada de função for usada como uma expressão, o valor de retorno é o valor da expressão.
função com resultado
Uma função que devolve um valor.
função nula
Uma função que sempre devolve None.
None
Um valor especial apresentado por funções nulas.
módulo
Um arquivo que contém uma coleção de funções relacionadas e outras definições.
instrução de importação
Uma instrução que lê um arquivo de módulo e cria um objeto de módulo.
objeto de módulo
Um valor criado por uma instrução import que oferece acesso aos valores definidos em um módulo.
notação de ponto
A sintaxe para chamar uma função em outro módulo especificando o nome do módulo seguido de um ponto e o nome da função.
composição
O uso de uma expressão como parte de uma expressão maior ou de uma instrução como parte de uma instrução maior.
fluxo de execução
A ordem na qual as instruções são executadas.
diagrama da pilha
Representação gráfica de uma pilha de funções, suas variáveis e os valores a que se referem.
frame
Uma caixa em um diagrama da pilha que representa uma chamada de função. Contém as variáveis locais e os parâmetros da função.
traceback
Lista das funções que estão sendo executadas, exibidas quando ocorre uma exceção.
3.14 - Exercícios
Exercício 3.1
Escreva uma função chamada right_justify, que receba uma string chamada s como parâmetro e exiba a string com espaços suficientes à frente para que a última letra da string esteja na coluna 70 da tela:
>>> right_justify('monty')
monty
Dica: Use concatenação de strings e repetição. Além disso, o Python oferece uma função integrada chamada len, que apresenta o comprimento de uma string, então o valor de len('monty') é 5.
Exercício 3.2
Um objeto de função é um valor que pode ser atribuído a uma variável ou passado como argumento. Por exemplo, do_twice é uma função que toma um objeto de função como argumento e o chama duas vezes:
def do_twice(f):
f()
f()
Aqui está um exemplo que usa do_twice para chamar uma função chamada print_spam duas vezes:
def print_spam():
print('spam')
do_twice(print_spam)
-
Digite este exemplo em um script e teste-o.
-
Altere
do_twicepara que receba dois argumentos, um objeto de função e um valor, e chame a função duas vezes, passando o valor como um argumento. -
Copie a definição de
print_twiceque aparece anteriormente neste capítulo no seu script. -
Use a versão alterada de
do_twicepara chamarprint_twiceduas vezes, passando'spam'como um argumento. -
Defina uma função nova chamada
do_fourque receba um objeto de função e um valor e chame a função quatro vezes, passando o valor como um parâmetro. Deve haver só duas afirmações no corpo desta função, não quatro.
Solução: http://thinkpython2.com/code/do_four.py.
Exercício 3.3
Nota: Este exercício deve ser feito usando-se apenas as instruções e os outros recursos que aprendemos até agora.
- Escreva uma função que desenhe uma grade como a seguinte:
+ - - - - + - - - - +
| | |
| | |
| | |
| | |
+ - - - - + - - - - +
| | |
| | |
| | |
| | |
+ - - - - + - - - - +
Dica: para exibir mais de um valor em uma linha, podemos usar uma sequência de valores separados por vírgula:
print('+', '-')Por padrão, print avança para a linha seguinte, mas podemos ignorar esse comportamento e inserir um espaço no fim, desta forma:
print('+', end=' ') print('-')A saída dessas instruções é
+ -. Uma instrução
- Escreva uma função que desenhe uma grade semelhante com quatro linhas e quatro colunas.
Solução: http://thinkpython2.com/code/grid.py. Crédito: Este exercício é baseado em outro apresentado por Oualline, em Practical C Programming, Third Edition, O’Reilly Media, 1997.
Capítulo 4: Estudo de caso: projeto de interface
Este capítulo apresenta um estudo de caso que demonstra o processo de criação de funções que operam simultaneamente.
Ele apresenta o módulo turtle, que permite criar imagens usando [turtle graphics][1]. O módulo turtle é incluído na maior parte das instalações do Python, mas se estiver executando a linguagem com o PythonAnywhere você não poderá executar os exemplos do turtle (pelo menos não era possível quando escrevi este livro).
Se já tiver instalado o Python no seu computador, você poderá executar os exemplos. Caso não, agora é uma boa hora para instalar. Publiquei instruções no site http://tinyurl.com/thinkpython2e.
Os exemplos de código deste capítulo estão disponíveis em http://thinkpython2.com/code/polygon.py.
4.1 - Módulo turtle
Para conferir se você tem o módulo turtle, abra o interpretador do Python e digite:
>>> import turtle
>>> bob = turtle.Turtle()
Ao executar este código o programa deve abrir uma nova janela com uma pequena flecha que representa o turtle. Feche a janela.
Crie um arquivo chamado mypolygon.py e digite o seguinte código:
import turtle
bob = turtle.Turtle()
print(bob)
turtle.mainloop()
O módulo turtle (com t minúsculo) apresenta uma função chamada Turtle (com T maiúsculo), que cria um objeto Turtle, ao qual atribuímos uma variável chamada bob. Exibir bob faz algo assim:
<turtle.Turtle object at 0xb7bfbf4c>
Isto significa que bob se refere a um objeto com o tipo Turtle definido no módulo turtle.
mainloop diz que a janela deve esperar que o usuário faça algo, embora neste caso não haja muito a fazer, exceto fechar a janela.
Uma vez que tenha criado o Turtle, você pode chamar um método para movê-lo pela janela. Método é semelhante a uma função, mas usa uma sintaxe ligeiramente diferente. Por exemplo, para mover o turtle para a frente:
bob.fd(100)
O método fd é associado com o objeto turtle, que denominamos bob. Chamar de um método é como fazer um pedido: você está pedindo que bob avance.
O argumento de fd é uma distância em píxeis, então o tamanho real depende da sua tela.
Outros métodos que você pode chamar em um Turtle são bk para mover-se para trás, lt para virar à esquerda e rt para virar à direita. O argumento para lt e rt é um ângulo em graus.
Além disso, cada Turtle segura uma caneta, que está abaixada ou levantada; se a caneta estiver abaixada, o Turtle deixa um rastro quando se move. Os métodos pu e pd representam “caneta para cima” e “caneta para baixo”.
Para desenhar um ângulo reto, acrescente estas linhas ao programa (depois de criar bob e antes de chamar o mainloop):
bob.fd(100)
bob.lt(90)
bob.fd(100)
Ao executar este programa, você deveria ver bob mover-se para o leste e depois para o norte, deixando dois segmentos de reta para trás.
Agora altere o programa para desenhar um quadrado. Só siga adiante neste capítulo se ele funcionar adequadamente!
4.2 - Repetição simples
Provavelmente você escreveu algo assim:
bob.fd(100)
bob.lt(90)
bob.fd(100)
bob.lt(90)
bob.fd(100)
bob.lt(90)
bob.fd(100)
Podemos fazer a mesma coisa de forma mais concisa com uma instrução for. Acrescente este exemplo a mypolygon.py e execute-o novamente:
for i in range(4):
print('Hello!')
Você deve ver algo assim:
Hello!
Hello!
Hello!
Hello!
Este é o uso mais simples da instrução for; depois veremos mais sobre isso. Mas isso deve ser o suficiente para que você possa reescrever o seu programa de desenhar quadrados. Não continue a leitura até que dê certo.
Aqui está uma instrução for que desenha um quadrado:
for i in range(4):
bob.fd(100)
bob.lt(90)
A sintaxe de uma instrução for é semelhante à definição de uma função. Tem um cabeçalho que termina em dois pontos e um corpo endentado. O corpo pode conter qualquer número de instruções.
Uma instrução for também é chamada de loop porque o fluxo da execução passa pelo corpo e depois volta ao topo. Neste caso, ele passa pelo corpo quatro vezes.
Esta versão, na verdade, é um pouco diferente do código anterior que desenha quadrados porque faz outra volta depois de desenhar o último lado do quadrado. A volta extra leva mais tempo, mas simplifica o código se fizermos a mesma coisa a cada vez pelo loop. Esta versão também tem o efeito de trazer o turtle de volta à posição inicial, de frente para a mesma direção em que estava.
4.3 - Exercícios
A seguir, uma série de exercícios usando TurtleWorld. Eles servem para divertir, mas também têm outro objetivo. Enquanto trabalha neles, pense que objetivo pode ser.
As seções seguintes têm as soluções para os exercícios, mas não olhe até que tenha terminado (ou, pelo menos, tentado).
- Escreva uma função chamada square que receba um parâmetro chamado t, que é um turtle. Ela deve usar o turtle para desenhar um quadrado.
Escreva uma chamada de função que passe bob como um argumento para o square e então execute o programa novamente.
-
Acrescente outro parâmetro, chamado length, ao square. Altere o corpo para que o comprimento dos lados seja length e então altere a chamada da função para fornecer um segundo argumento. Execute o programa novamente. Teste o seu programa com uma variedade de valores para length.
-
Faça uma cópia do square e mude o nome para polygon. Acrescente outro parâmetro chamado n e altere o corpo para que desenhe um polígono regular de n lados.
Dica: os ângulos exteriores de um polígono regular de n lados são 360/n graus.
- Escreva uma função chamada circle que use o turtle, t e um raio r como parâmetros e desenhe um círculo aproximado ao chamar polygon com um comprimento e número de lados adequados. Teste a sua função com uma série de valores de r.
Dica: descubra a circunferência do círculo e certifique-se de que length * n = circumference.
- Faça uma versão mais geral do circle chamada arc, que receba um parâmetro adicional de angle, para determinar qual fração do círculo deve ser desenhada. angle está em unidades de graus, então quando angle=360, o arc deve desenhar um círculo completo.
4.4 - Encapsulamento
O primeiro exercício pede que você ponha seu código para desenhar quadrados em uma definição de função e então chame a função, passando o turtle como parâmetro. Aqui está uma solução:
def square(t):
for i in range(4):
t.fd(100)
t.lt(90)
square(bob)
As instruções mais internas, fd e lt, são endentadas duas vezes para mostrar que estão dentro do loop for, que está dentro da definição da função. A linha seguinte, square(bob), está alinhada à margem esquerda, o que indica tanto o fim do loop for como da definição de função.
Dentro da função, o t indica o mesmo turtle bob, então t.lt (90) tem o mesmo efeito que bob.lt (90). Neste caso, por que não chamar o parâmetro bob? A ideia é que t pode ser qualquer turtle, não apenas bob, então você pode criar um segundo turtle e passá-lo como argumento ao square:
alice = turtle.Turtle()
square(alice)
Incluir uma parte do código em uma função chama-se encapsulamento. Um dos benefícios do encapsulamento é que ele atribui um nome ao código, o que serve como uma espécie de documentação. Outra vantagem é que se você reutilizar o código, é mais conciso chamar uma função duas vezes que copiar e colar o corpo!
4.5 - Generalização
O próximo passo é acrescentar um parâmetro length ao square. Aqui está uma solução:
def square(t, length):
for i in range(4):
t.fd(length)
t.lt(90)
square(bob, 100)
Acrescentar um parâmetro a uma função chama-se generalização porque ele torna a função mais geral: na versão anterior, o quadrado é sempre do mesmo tamanho; nesta versão, pode ser de qualquer tamanho.
O próximo passo também é uma generalização. Em vez de desenhar quadrados, polygon desenha polígonos regulares com qualquer número de lados. Aqui está uma solução:
def polygon(t, n, length):
angle = 360 / n
for i in range(n):
t.fd(length)
t.lt(angle)
polygon(bob, 7, 70)
Este exemplo desenha um polígono de 7 lados, cada um de comprimento 70.
Se estiver usando Python 2, o valor do angle poderia estar errado por causa da divisão de número inteiro. Uma solução simples é calcular angle = 360.0 / n. Como o numerador é um número de ponto flutuante, o resultado é em ponto flutuante.
Quando uma função tem vários argumentos numéricos, é fácil esquecer o que eles são ou a ordem na qual eles devem estar. Neste caso, muitas vezes é uma boa ideia incluir os nomes dos parâmetros na lista de argumentos:
polygon (bob, n=7, length=70)
Esses são os argumentos de palavra-chave porque incluem os nomes dos parâmetros como “palavras-chave” (para não confundir com palavras-chave do Python, tais como while e def).
Esta sintaxe torna o programa mais legível. Também é uma lembrança sobre como os argumentos e os parâmetros funcionam: quando você chama uma função, os argumentos são atribuídos aos parâmetros.
4.6 - Projeto da interface
O próximo passo é escrever circle, que recebe um raio r, como parâmetro. Aqui está uma solução simples que usa o polygon para desenhar um polígono de 50 lados:
import math
def circle(t, r):
circumference = 2 * math.pi * r
n = 50
length = circumference / n
polygon(t, n, length)
A primeira linha calcula a circunferência de um círculo com o raio r usando a fórmula 2πr. Já que usamos math.pi, temos que importar math. Por convenção, instruções import normalmente ficam no início do script.
n é o número de segmentos de reta na nossa aproximação de um círculo, então length é o comprimento de cada segmento. Assim, polygon desenha um polígono 50 lados que se aproxima de um círculo com o raio r.
Uma limitação desta solução é que n é uma constante. Para círculos muito grandes, os segmentos de reta são longos demais, e para círculos pequenos, perdemos tempo desenhando segmentos muito pequenos. Uma solução seria generalizar a função tomando n como parâmetro. Isso daria ao usuário (seja quem for que chame circle) mais controle, mas a interface seria menos limpa.
A interface de uma função é um resumo de como ela é usada: Quais são os parâmetros? O que a função faz? E qual é o valor de retorno? Uma interface é “limpa” se permitir à pessoa que a chama fazer o que quiser sem ter que lidar com detalhes desnecessários.
Neste exemplo, r pertence à interface porque especifica o círculo a ser desenhado. n é menos adequado porque pertence aos detalhes de como o círculo deve ser apresentado.
Em vez de poluir a interface, é melhor escolher um valor adequado para n, dependendo da circumference:
def circle(t, r):
circumference = 2 * math.pi * r
n = int(circumference / 3) + 1
length = circumference / n
polygon(t, n, length)
Neste ponto, o número de segmentos é um número inteiro próximo a circumference/3, então o comprimento de cada segmento é aproximadamente 3, pequeno o suficiente para que os círculos fiquem bons, mas grandes o suficiente para serem eficientes e aceitáveis para círculos de qualquer tamanho.
4.7 - Refatoração
Quando escrevi circle, pude reutilizar polygon porque um polígono de muitos lados é uma boa aproximação de um círculo. Mas o arc não é tão cooperativo; não podemos usar polygon ou circle para desenhar um arco.
Uma alternativa é começar com uma cópia de polygon e transformá-la em arc. O resultado poderia ser algo assim:
def arc(t, r, angle):
arc_length = 2 * math.pi * r * angle / 360
n = int(arc_length / 3) + 1
step_length = arc_length / n
step_angle = angle / n
for i in range(n):
t.fd(step_length)
t.lt(step_angle)
A segunda metade desta função parece com a do polygon, mas não é possível reutilizar o polygon sem mudar a interface. Poderíamos generalizar polygon para receber um ângulo como um terceiro argumento, mas então polygon não seria mais um nome adequado! Em vez disso, vamos chamar a função mais geral de polyline:
def polyline(t, n, length, angle):
for i in range(n):
t.fd(length)
t.lt(angle)
Agora podemos reescrever polygon e arc para usar polyline:
def polygon(t, n, length):
angle = 360.0 / n
polyline(t, n, length, angle)
def arc(t, r, angle):
arc_length = 2 * math.pi * r * angle / 360
n = int(arc_length / 3) + 1
step_length = arc_length / n
step_angle = float(angle) / n
polyline(t, n, step_length, step_angle)
Finalmente, podemos reescrever circle para usar arc:
def circle(t, r):
arc(t, r, 360)
Este processo – recompor um programa para melhorar interfaces e facilitar a reutilização do código – é chamado de refatoração. Neste caso, notamos que houve código semelhante em arc e polygon, então nós o “fatoramos” no polyline.
Se tivéssemos planejado, poderíamos ter escrito polyline primeiro e evitado a refatoração, mas muitas vezes não sabemos o suficiente já no início de um projeto para projetar todas as interfaces. Quando começarmos a escrever código, entenderemos melhor o problema. Às vezes, a refatoração é um sinal de que aprendemos algo.
4.8 - Um plano de desenvolvimento
Um plano de desenvolvimento é um processo para escrever programas. O processo que usamos neste estudo de caso é “encapsulamento e generalização”. Os passos deste processo são:
-
Comece escrevendo um pequeno programa sem definições de função.
-
Uma vez que o programa esteja funcionando, identifique uma parte coerente dele, encapsule essa parte em uma função e dê um nome a ela.
-
Generalize a função acrescentando os parâmetros adequados.
-
Repita os passos 1-3 até que tenha um conjunto de funções operantes. Copie e cole o código operante para evitar a redigitação (e redepuração).
-
Procure oportunidades de melhorar o programa pela refatoração. Por exemplo, se você tem um código semelhante em vários lugares, pode ser uma boa ideia fatorá-lo em uma função geral adequada.
Este processo tem algumas desvantagens – veremos alternativas mais tarde – mas pode ser útil se você não souber de antemão como dividir o programa em funções. Esta abordagem permite criar o projeto no decorrer do trabalho.
4.9 - docstring
Uma docstring é uma string no início de uma função que explica a interface (“doc” é uma abreviação para “documentação”). Aqui está um exemplo:
def polyline(t, n, length, angle):
"""Desenha n segmentos de reta com o comprimento dado e
ângulo (em graus) entre eles. t é um turtle.
"""
for i in range(n):
t.fd(length)
t.lt(angle)
Por convenção, todas as docstrings têm aspas triplas, também conhecidas como strings multilinha porque as aspas triplas permitem que a string se estenda por mais de uma linha.
É conciso, mas contém a informação essencial que alguém precisaria para usar esta função. Explica sucintamente o que a função faz (sem entrar nos detalhes de como o faz). Explica que efeito cada parâmetro tem sobre o comportamento da função e o tipo que cada parâmetro deve ser (se não for óbvio).
Escrever este tipo de documentação é uma parte importante do projeto da interface. Uma interface bem projetada deve ser simples de explicar; se não for assim, talvez a interface possa ser melhorada.
4.10 - Depuração
Uma interface é como um contrato entre uma função e quem a chama. Quem chama concorda em fornecer certos parâmetros e a função concorda em fazer certa ação.
Por exemplo, polyline precisa de quatro argumentos: t tem que ser um Turtle; n tem que ser um número inteiro; length deve ser um número positivo; e o angle tem que ser um número, que se espera estar em graus.
Essas exigências são chamadas de precondições porque se supõe que sejam verdade antes que a função seja executada. De forma inversa, as condições no fim da função são pós-condições. As pós-condições incluem o efeito desejado da função (como o desenho de segmentos de reta) e qualquer efeito colateral (como mover o Turtle ou fazer outras mudanças).
Precondições são responsabilidade de quem chama. Se quem chama violar uma precondição (adequadamente documentada!) e a função não funcionar corretamente, o problema está nesta pessoa, não na função.
Se as precondições forem satisfeitas e as pós-condições não forem, o problema está na função. Se as suas precondições e pós-condições forem claras, elas podem ajudar na depuração.
4.11 - Glossário
método
Uma função associada a um objeto e chamada usando a notação de ponto.
loop
Parte de um programa que pode ser executada repetidamente.
encapsulamento
O processo de transformar uma sequência de instruções em uma definição de função.
generalização
O processo de substituir algo desnecessariamente específico (como um número) por algo adequadamente geral (como uma variável ou parâmetro).
argumento de palavra-chave
Um argumento que inclui o nome do parâmetro como uma “palavra-chave”.
interface
Uma descrição de como usar uma função, incluindo o nome e as descrições dos argumentos e do valor de retorno.
refatoração
O processo de alterar um programa funcional para melhorar a interface de funções e outras qualidades do código.
plano de desenvolvimento
Um processo de escrever programas.
docstring
Uma string que aparece no início de uma definição de função para documentar a interface da função.
precondição
Uma exigência que deve ser satisfeita por quem chama a função, antes de executá-la.
pós-condição
Uma exigência que deve ser satisfeita pela função antes que ela seja encerrada.
4.12 - Exercícios
Exercício 4.1
Baixe o código deste capítulo no site http://thinkpython2.com/code/polygon.py.
-
Desenhe um diagrama da pilha que mostre o estado do programa enquanto executa circle (bob, radius). Você pode fazer a aritmética à mão ou acrescentar instruções print ao código.
-
A versão de
arcna seção 4.7 - Refatoração não é muito precisa porque a aproximação linear do círculo está sempre do lado de fora do círculo verdadeiro. Consequentemente, o Turtle acaba ficando alguns píxeis de distância do destino correto. Minha solução mostra um modo de reduzir o efeito deste erro. Leia o código e veja se faz sentido para você. Se desenhar um diagrama, poderá ver como funciona.
Exercício 4.2
Escreva um conjunto de funções adequadamente geral que possa desenhar flores como as da Figura 4.1.
 .
.
Figura 4.1 – Flores de tartaruga.
Solução: http://thinkpython2.com/code/flower.py, também exige http://thinkpython2.com/code/polygon.py.
Exercício 4.3
Escreva um conjunto de funções adequadamente geral que possa desenhar formas como as da Figura 4.2.
 .
.
Figura 4.2 – Tortas de tartaruga.
Solução: http://thinkpython2.com/code/pie.py.
Exercício 4.4
As letras do alfabeto podem ser construídas a partir de um número moderado de elementos básicos, como linhas verticais e horizontais e algumas curvas. Crie um alfabeto que possa ser desenhado com um número mínimo de elementos básicos e então escreva funções que desenhem as letras.
Você deve escrever uma função para cada letra, com os nomes draw_a, draw_b etc., e colocar suas funções em um arquivo chamado letters.py. Você pode baixar uma “máquina de escrever de turtle” no site http://thinkpython2.com/code/typewriter.py para ajudar a testar o seu código.
Você pode ver uma solução no site http://thinkpython2.com/code/letters.py; ela também exige http://thinkpython2.com/code/polygon.py.
Exercício 4.5
Leia sobre espirais em https://pt.wikipedia.org/wiki/Espiral; então escreva um programa que desenhe uma espiral de Arquimedes (ou um dos outros tipos).
[1] turtle graphics ou gráficos de tartaruga é o sistema de desenho popularizado pela linguagem Logo, onde os comandos movimentam um cursor triangular pela tela, conhecido como turtle ou tartaruga. A tartaruga deixa um rastro à medida que é movimentada, e é com esses rastros que se forma um desenho. Diferente dos sistemas usuais de desenho em computação gráfica, o sistema turtle graphics não exige o uso de coordenadas cartesianas.
Capítulo 5: Condicionais e recursividade
O tópico principal deste capítulo é a instrução if, que executa códigos diferentes dependendo do estado do programa. Mas primeiro quero apresentar dois novos operadores: divisão pelo piso e módulo.
5.1 - Divisão pelo piso e módulo
O operador de divisão pelo piso, //, divide dois números e arredonda o resultado para um número inteiro para baixo. Por exemplo, suponha que o tempo de execução de um filme seja de 105 minutos. Você pode querer saber a quanto isso corresponde em horas. A divisão convencional devolve um número de ponto flutuante:
>>> minutes = 105
>>> minutes / 60
1.75
Mas não é comum escrever horas com pontos decimais. A divisão pelo piso devolve o número inteiro de horas, ignorando a parte fracionária:
>>> minutes = 105
>>> hours = minutes // 60
>>> hours
1
Para obter o resto, você pode subtrair uma hora em minutos:
>>> remainder = minutes - hours * 60
>>> remainder
45
Uma alternativa é usar o operador módulo, %, que divide dois números e devolve o resto:
>>> remainder = minutes % 60
>>> remainder
45
O operador módulo é mais útil do que parece. Por exemplo, é possível verificar se um número é divisível por outro – se x % y for zero, então x é divisível por y.
Além disso, você pode extrair o dígito ou dígitos mais à direita de um número. Por exemplo, x % 10 produz o dígito mais à direita de x (na base 10). Da mesma forma x % 100 produz os dois últimos dígitos.
Se estiver usando o Python 2, a divisão funciona de forma diferente. O operador de divisão, /, executa a divisão pelo piso se ambos os operandos forem números inteiros e faz a divisão de ponto flutuante se pelo menos um dos operandos for do tipo float.
5.2 - Expressões booleanas
Uma expressão booleana é uma expressão que pode ser verdadeira ou falsa. Os exemplos seguintes usam o operador ==, que compara dois operandos e produz True se forem iguais e False se não forem:
>>> 5 == 5
True
>>> 5 == 6
False
True e False são valores especiais que pertencem ao tipo bool; não são strings:
>>> type(True)
<class 'bool'>
>>> type(False)
<class 'bool'>
O operador == é um dos operadores relacionais; os outros são:
x != y # x não é igual a y
x > y # x é maior que y
x < y # x é menor que y
x >= y # x é maior ou igual a y
x <= y # x é menor ou igual a y
Embora essas operações provavelmente sejam familiares para você, os símbolos do Python são diferentes dos símbolos matemáticos. Um erro comum é usar apenas um sinal de igual (=) em vez de um sinal duplo (==). Lembre-se de que = é um operador de atribuição e == é um operador relacional. Não existe =< ou =>.
5.3 - Operadores lógicos
Há três operadores lógicos: and, or e not. A semântica (significado) destes operadores é semelhante ao seu significado em inglês. Por exemplo, x> 0 and x <10 só é verdade se x for maior que 0 e menor que 10.
n%2 == 0 or n%3 == 0 é verdadeiro se uma ou as duas condição(ões) for(em) verdadeira(s), isto é, se o número for divisível por 2 ou 3.
Finalmente, o operador not nega uma expressão booleana, então not (x > y) é verdade se x > y for falso, isto é, se x for menor que ou igual a y.
Falando estritamente, os operandos dos operadores lógicos devem ser expressões booleanas, mas o Python não é muito estrito. Qualquer número que não seja zero é interpretado como True:
>>> 42 and True
True
Esta flexibilidade tem sua utilidade, mas há algumas sutilezas relativas a ela que podem ser confusas. Assim, pode ser uma boa ideia evitá-la (a menos que saiba o que está fazendo).
5.4 - Execução condicional
Para escrever programas úteis, quase sempre precisamos da capacidade de verificar condições e mudar o comportamento do programa de acordo com elas. Instruções condicionais nos dão esta capacidade. A forma mais simples é a instrução if:
if x > 0:
print('x is positive')
A expressão booleana depois do if é chamada de condição. Se for verdadeira, a instrução endentada é executada. Se não, nada acontece.
Instruções if têm a mesma estrutura que definições de função: um cabeçalho seguido de um corpo endentado. Instruções como essa são chamadas de instruções compostas.
Não há limite para o número de instruções que podem aparecer no corpo, mas deve haver pelo menos uma. Ocasionalmente, é útil ter um corpo sem instruções (normalmente como um espaço reservado para código que ainda não foi escrito). Neste caso, você pode usar a instrução pass, que não faz nada.
if x < 0:
pass # A FAZER: lidar com valores negativos!
5.5 - Execução alternativa
Uma segunda forma da instrução if é a “execução alternativa”, na qual há duas possibilidades e a condição determina qual será executada. A sintaxe pode ser algo assim:
if x % 2 == 0:
print('x is even')
else:
print('x is odd')
Se o resto quando x for dividido por 2 for 0, então sabemos que x é par e o programa exibe uma mensagem adequada. Se a condição for falsa, o segundo conjunto de instruções é executado. Como a condição deve ser verdadeira ou falsa, exatamente uma das alternativas será executada. As alternativas são chamadas de ramos (branches), porque são ramos no fluxo da execução.
5.6 - Condicionais encadeadas
Às vezes, há mais de duas possibilidades e precisamos de mais que dois ramos. Esta forma de expressar uma operação de computação é uma condicional encadeada:
if x < y:
print('x is less than y')
elif x > y:
print('x is greater than y')
else:
print('x and y are equal')
elif é uma abreviatura de “else if”. Novamente, exatamente um ramo será executado. Não há nenhum limite para o número de instruções elif. Se houver uma cláusula else, ela deve estar no fim, mas não é preciso haver uma.
if choice == 'a':
draw_a()
elif choice == 'b':
draw_b()
elif choice == 'c':
draw_c()
Cada condição é verificada em ordem. Se a primeira for falsa, a próxima é verificada, e assim por diante. Se uma delas for verdadeira, o ramo correspondente é executado e a instrução é encerrada. Mesmo se mais de uma condição for verdade, só o primeiro ramo verdadeiro é executado.
5.7 - Condicionais aninhadas
Uma condicional também pode ser aninhada dentro de outra. Poderíamos ter escrito o exemplo na seção anterior desta forma:
if x == y:
print('x and y are equal')
else:
if x < y:
print('x is less than y')
else:
print('x is greater than y')
A condicional exterior contém dois ramos. O primeiro ramo contém uma instrução simples. O segundo ramo contém outra instrução if, que tem outros dois ramos próprios. Esses dois ramos são instruções simples, embora pudessem ser instruções condicionais também.
Embora a endentação das instruções evidencie a estrutura das condicionais, condicionais aninhadas são difíceis de ler rapidamente. É uma boa ideia evitá-las quando for possível.
Operadores lógicos muitas vezes oferecem uma forma de simplificar instruções condicionais aninhadas. Por exemplo, podemos reescrever o seguinte código usando uma única condicional:
if 0 < x:
if x < 10:
print('x is a positive single-digit number.')
A instrução print só é executada se a colocarmos depois de ambas as condicionais, então podemos obter o mesmo efeito com o operador and:
if 0 < x and x < 10:
print('x is a positive single-digit number.')
Para este tipo de condição, o Python oferece uma opção mais concisa:
if 0 < x < 10:
print('x is a positive single-digit number.')
5.8 - Recursividade
É legal para uma função chamar outra; também é legal para uma função chamar a si própria. Pode não ser óbvio porque isso é uma coisa boa, mas na verdade é uma das coisas mais mágicas que um programa pode fazer. Por exemplo, veja a seguinte função:
def countdown(n):
if n <= 0:
print('Blastoff!')
else:
print(n)
countdown(n-1)
Se n for 0 ou negativo, a palavra “Blastoff!” é exibida, senão a saída é n e então a função countdown é chamada – por si mesma – passando n-1 como argumento.
O que acontece se chamarmos esta função assim?
>>> countdown(3)
A execução de countdown inicia com n=3 e como n é maior que 0, ela produz o valor 3 e então chama a si mesma...
A execução de countdown inicia com n=2 e como n é maior que 0, ela produz o valor 2 e então chama a si mesma...
A execução de countdown inicia com n=1 e como n é maior que 0, ela produz o valor 1 e então chama a si mesma...
A execução de countdown inicia com n=0 e como n não é maior que 0, ela produz a palavra “Blastoff!” e então retorna.
O countdown que recebeu n=1 retorna.
O countdown que recebeu n=2 retorna.
O countdown que recebeu n=3 retorna.
E então você está de volta ao __main__. Então a saída completa será assim:
3
2
1
Blastoff!
Uma função que chama a si mesma é dita recursiva; o processo para executá-la é a recursividade.
Como em outro exemplo, podemos escrever uma função que exiba uma string n vezes:
def print_n(s, n):
if n <= 0:
return
print(s)
print_n(s, n-1)
Se n <= 0 a instrução return causa a saída da função. O fluxo de execução volta imediatamente a quem fez a chamada, e as linhas restantes da função não são executadas.
O resto da função é similar à countdown: ela mostra s e então chama a si mesma para mostrar s mais n-1 vezes. Então o número de linhas da saída é 1 + (n - 1), até chegar a n.
Para exemplos simples como esse, provavelmente é mais fácil usar um loop for. Mais adiante veremos exemplos que são difíceis de escrever com um loop for e fáceis de escrever com recursividade, então é bom começar cedo.
5.9 - Diagramas da pilha para funções recursivas
Em “Diagrama da pilha”, na página 55, usamos um diagrama da pilha para representar o estado de um programa durante uma chamada de função. O mesmo tipo de diagrama pode ajudar a interpretar uma função recursiva.
Cada vez que uma função é chamada, o Python cria um frame para conter as variáveis locais e parâmetros da função. Para uma função recursiva, pode haver mais de um frame na pilha ao mesmo tempo.
A Figura 5.1 mostra um diagrama da pilha para countdown chamado com n = 3.
 .
.
Figura 5.1 – Diagrama da pilha.
Como de hábito, o topo da pilha é o frame de __main__. Está vazio porque não criamos nenhuma variável em __main__ nem passamos argumentos a ela.
Os quatro frames do countdown têm valores diferentes para o parâmetro n. O fundo da pilha, onde n = 0, é chamado caso-base. Ele não faz uma chamada recursiva, então não há mais frames.
Como exercício, desenhe um diagrama da pilha para print_n chamado com s = 'Hello' e n = 2. Então escreva uma função chamada do_n que tome um objeto de função e um número n como argumentos e que chame a respectiva função n vezes.
5.10 - Recursividade infinita
Se a recursividade nunca atingir um caso-base, continua fazendo chamadas recursivas para sempre, e o programa nunca termina. Isso é conhecido como recursividade infinita e geralmente não é uma boa ideia. Aqui está um programa mínimo com recursividade infinita:
def recurse():
recurse()
Na maior parte dos ambientes de programação, um programa com recursividade infinita não é realmente executado para sempre. O Python exibe uma mensagem de erro quando a profundidade máxima de recursividade é atingida:
File "<stdin>", line 2, in recurse
File "<stdin>", line 2, in recurse
File "<stdin>", line 2, in recurse
.
.
.
File "<stdin>", line 2, in recurse
RuntimeError: Maximum recursion depth exceeded
Este traceback é um pouco maior que o que vimos no capítulo anterior. Quando o erro ocorre, há mil frames de recurse na pilha!
Se você escrever em recursividade infinita por engano, confira se a sua função tem um caso-base que não faz uma chamada recursiva. E se houver um caso-base, verifique se você vai mesmo atingi-lo.
5.11 - Entrada de teclado
Os programas que escrevemos até agora não aceitam entradas do usuário. Eles sempre fazem a mesma coisa cada vez.
O Python fornece uma função integrada chamada input que interrompe o programa e espera que o usuário digite algo. Quando o usuário pressionar Return ou Enter, o programa volta a ser executado e input retorna o que o usuário digitou como uma string. No Python 2, a mesma função é chamada raw_input.
>>> text = input()
What are you waiting for?
>>> text
What are you waiting for?
Antes de receber entradas do usuário, é uma boa ideia exibir um prompt dizendo ao usuário o que ele deve digitar. input pode ter um prompt como argumento:
>>> name = input('What...is your name?\\n')
What...is your name?
Arthur, King of the Britons!
>>> name
Arthur, King of the Britons!
A sequência \n no final do prompt representa um newline, que é um caractere especial de quebra de linha. É por isso que a entrada do usuário aparece abaixo do prompt.
Se esperar que o usuário digite um número inteiro, você pode tentar converter o valor de retorno para int:
>>> prompt = 'What...is the airspeed velocity of an unladen swallow?\\n'
>>> speed = input(prompt)
What...is the airspeed velocity of an unladen swallow?
42
>>> int(speed)
42
Mas se o usuário digitar algo além de uma série de dígitos, você recebe um erro:
>>> speed = input(prompt)
What...is the airspeed velocity of an unladen swallow?
What do you mean, an African or a European swallow?
>>> int(speed)
ValueError: invalid literal for int() with base 10
Veremos como tratar este tipo de erro mais adiante.
5.12 - Depuração
Quando um erro de sintaxe ou de tempo de execução ocorre, a mensagem de erro contém muita informação, às vezes, até demais. As partes mais úteis são normalmente:
-
que tipo de erro foi;
-
onde ocorreu.
Erros de sintaxe são normalmente fáceis de encontrar, mas há algumas pegadinhas. Erros de whitespace podem ser complicados porque os espaços e tabulações são invisíveis e estamos acostumados a ignorá-los.
>>> x = 5
>>> y = 6
File "<stdin>", line 1
y = 6
^
IndentationError: unexpected indent
Neste exemplo, o problema é que a segunda linha está endentada por um espaço. Mas a mensagem de erro aponta para y, o que pode ser capcioso. Em geral, mensagens de erro indicam onde o problema foi descoberto, mas o erro real pode estar em outra parte do código, às vezes, em uma linha anterior.
O mesmo acontece com erros em tempo de execução. Suponha que você esteja tentando calcular a proporção de sinal a ruído em decibéis. A fórmula é SNRdb = 10 log10 (Psignal/Pnoise). No Python, você poderia escrever algo assim:
import math
signal_power = 9
noise_power = 10
ratio = signal_power // noise_power
decibels = 10 * math.log10(ratio)
print(decibels)
Ao executar este programa, você recebe uma exceção:
Traceback (most recent call last):
File "snr.py", line 5, in ?
decibels = 10 * math.log10(ratio)
ValueError: math domain error
A mensagem de erro indica a linha 5, mas não há nada de errado com esta linha. Uma opção para encontrar o verdadeiro erro é exibir o valor de ratio, que acaba sendo 0. O problema está na linha 4, que usa a divisão pelo piso em vez da divisão de ponto flutuante.
É preciso ler as mensagens de erro com atenção, mas não assumir que tudo que dizem esteja correto.
5.13 - Glossário
divisão pelo piso
Um operador, denotado por //, que divide dois números e arredonda o resultado para baixo (em direção ao zero), a um número inteiro.
operador módulo
Um operador, denotado com um sinal de percentagem (%), que funciona com números inteiros e devolve o resto quando um número é dividido por outro.
expressão booleana
Uma expressão cujo valor é True (verdadeiro) ou False (falso).
operador relacional
Um destes operadores, que compara seus operandos: ==, !=, >, <, >= e <=.
operador lógico
Um destes operadores, que combina expressões booleanas: and (e), or (ou) e not (não).
instrução condicional
Uma instrução que controla o fluxo de execução, dependendo de alguma condição.
condição
A expressão booleana em uma instrução condicional que determina qual ramo deve ser executado.
instrução composta
Uma instrução composta de um cabeçalho e um corpo. O cabeçalho termina em dois pontos (:). O corpo é endentado em relação ao cabeçalho.
ramo
Uma das sequências alternativas de instruções em uma instrução condicional.
condicional encadeada
Uma instrução condicional com uma série de ramos alternativos.
condicional aninhada
Uma instrução condicional que aparece em um dos ramos de outra instrução condicional.
instrução de retorno
Uma instrução que faz uma função terminar imediatamente e voltar a quem a chamou.
recursividade
O processo de chamar a função que está sendo executada no momento.
caso-base
Um ramo condicional em uma função recursiva que não faz uma chamada recursiva.
recursividade infinita
Recursividade que não tem um caso-base, ou nunca o atinge. A recursividade infinita eventualmente causa um erro em tempo de execução.
5.14 - Exercícios
Exercício 5.1
O módulo time fornece uma função, também chamada time, que devolve a Hora Média de Greenwich na “época”, que é um momento arbitrário usado como ponto de referência. Em sistemas UNIX, a época é primeiro de janeiro de 1970.
>>> import time
>>> time.time()
1437746094.5735958
Escreva um script que leia a hora atual e a converta em um tempo em horas, minutos e segundos, mais o número de dias desde a época.
Exercício 5.2
O último teorema de Fermat diz que não existem números inteiros a, b e c tais que a**n + b**n == c**n para quaisquer valores de n maiores que 2.
-
Escreva uma função chamada check_fermat que receba quatro parâmetros – a, b, c e n – e verifique se o teorema de Fermat se mantém. Se n for maior que 2 e
a**n + b**n == c**no programa deve imprimir, “Holy smokes, Fermat was wrong!” Senão o programa deve exibir “No, that doesn’t work.” -
Escreva uma função que peça ao usuário para digitar valores para a, b, c e n, os converta em números inteiros e use check_fermat para verificar se violam o teorema de Fermat.
Exercício 5.3
Se você tiver três gravetos, pode ser que consiga arranjá-los em um triângulo ou não. Por exemplo, se um dos gravetos tiver 12 polegadas de comprimento e outros dois tiverem uma polegada de comprimento, não será possível fazer com que os gravetos curtos se encontrem no meio. Há um teste simples para ver se é possível formar um triângulo para quaisquer três comprimentos:
Se algum dos três comprimentos for maior que a soma dos outros dois, então você não pode formar um triângulo. Senão, você pode. (Se a soma de dois comprimentos igualar o terceiro, eles formam um triângulo chamado “degenerado”)
-
Escreva uma função chamada
is_triangleque receba três números inteiros como argumentos, e que imprima “Yes” ou “No”, dependendo da possibilidade de formar ou não um triângulo de gravetos com os comprimentos dados. -
Escreva uma função que peça ao usuário para digitar três comprimentos de gravetos, os converta em números inteiros e use
is_trianglepara verificar se os gravetos com os comprimentos dados podem formar um triângulo.
Exercício 5.4
Qual é a saída do seguinte programa? Desenhe um diagrama da pilha que mostre o estado do programa quando exibir o resultado.
def recurse(n, s):
if n == 0:
print(s)
else:
recurse(n-1, n+s)
recurse(3, 0)
-
O que aconteceria se você chamasse esta função desta forma: recurse(-1, 0)?
-
Escreva uma docstring que explique tudo o que alguém precisaria saber para usar esta função (e mais nada).
Os seguintes exercícios usam o módulo turtle, descrito no Capítulo 4:
Exercício 5.5
Leia a próxima função e veja se consegue compreender o que ela faz (veja os exemplos no Capítulo 4). Então execute-a e veja se acertou.
def draw(t, length, n):
if n == 0:
return
angle = 50
t.fd(length * n)
t.lt(angle)
draw(t, length, n-1)
t.rt(2 * angle)
draw(t, length, n-1)
t.lt(angle)
t.bk(length * n)
Exercício 5.6
 .
.
Figura 5.2 – Uma curva de Koch.
A curva de Koch é um fractal que parece com o da Figura 5.2. Para desenhar uma curva de Koch com o comprimento x, tudo o que você tem que fazer é:
-
Desenhe uma curva de Koch com o comprimento x/3.
-
Vire 60 graus à esquerda.
-
Desenhe uma curva de Koch com o comprimento x/3.
-
Vire 120 graus à direita.
-
Desenhe uma curva de Koch com o comprimento x/3.
-
Vire 60 graus à esquerda.
-
Desenhe uma curva de Koch com o comprimento x/3.
A exceção é se x for menor que 3: neste caso, você pode desenhar apenas uma linha reta com o comprimento x.
-
Escreva uma função chamada koch que receba um turtle e um comprimento como parâmetros, e use o turtle para desenhar uma curva de Koch com o comprimento dado.
-
Escreva uma função chamada snowflake que desenhe três curvas de Koch para fazer o traçado de um floco de neve.
Solução: http://thinkpython2.com/code/koch.py.
- A curva de Koch pode ser generalizada de vários modos. Veja exemplos em http://en.wikipedia.org/wiki/Koch_snowflake e implemente o seu favorito.
Capítulo 6: Funções com resultado
Muitas das funções do Python que usamos, como as matemáticas, produzem valores de retorno. Mas as funções que escrevemos até agora são todas nulas: têm um efeito, como exibir um valor ou mover uma tartaruga, mas não têm um valor de retorno. Neste capítulo você aprenderá a escrever funções com resultados.
6.1 - Valores de retorno
A chamada de função gera um valor de retorno, que normalmente atribuímos a uma variável ou usamos como parte de uma expressão.
e = math.exp(1.0)
height = radius * math.sin(radians)
As funções que descrevemos, por enquanto, são todas nulas. Resumindo, elas não têm valores de retorno; mais precisamente, o seu valor de retorno é None.
Neste capítulo veremos (finalmente) como escrever funções com resultados. O primeiro exemplo é area, que devolve a área de um círculo com o raio dado:
def area(radius):
a = math.pi * radius**2
return a
Já vimos a instrução return, mas em uma função com resultado ela inclui uma expressão. Esta instrução significa: “Volte imediatamente desta função e use a seguinte expressão como valor de retorno”. A expressão pode ser arbitrariamente complicada, então poderíamos ter escrito esta função de forma mais concisa:
def area(radius):
return math.pi * radius**2
Por outro lado, variáveis temporárias como a, tornam a depuração mais fácil.
Às vezes, é útil ter várias instruções de retorno, uma em cada ramo de uma condicional:
def absolute_value(x):
if x < 0:
return -x
else:
return x
Como essas instruções return estão em uma condicional alternativa, apenas uma é executada.
Logo que uma instrução de retorno seja executada, a função termina sem executar nenhuma instrução subsequente. Qualquer código que apareça depois de uma instrução return, ou em qualquer outro lugar que o fluxo da execução não atinja, é chamado de código morto.
Em uma função com resultado, é uma boa ideia garantir que cada caminho possível pelo programa atinja uma instrução return. Por exemplo:
def absolute_value(x):
if x < 0:
return -x
if x > 0:
return x
Essa função é incorreta porque se x for 0, nenhuma condição é verdade, e a função termina sem chegar a uma instrução return. Se o fluxo de execução chegar ao fim de uma função, o valor de retorno é None, que não é o valor absoluto de 0:
>>> absolute_value(0)
None
A propósito, o Python oferece uma função integrada chamada abs, que calcula valores absolutos.
Como exercício, escreva uma função compare que receba dois valores, x e y, e retorne 1 se x > y, 0 se x == y e -1 se x < y.
6.2 - Desenvolvimento incremental
Conforme você escrever funções maiores, pode ser que passe mais tempo as depurando.
Para lidar com programas cada vez mais complexos, você pode querer tentar usar um processo chamado de desenvolvimento incremental. A meta do desenvolvimento incremental é evitar longas sessões de depuração, acrescentando e testando pequenas partes do código de cada vez.
Como um exemplo, vamos supor que você queira encontrar a distância entre dois pontos dados pelas coordenadas (x1, y1) e(x2, y2). Pelo teorema de Pitágoras, a distância é:
 .
.
O primeiro passo é pensar como uma função distance deveria ser no Python. Em outras palavras, quais são as entradas (parâmetros) e qual é a saída (valor de retorno)?
Nesse caso, as entradas são dois pontos que você pode representar usando quatro números. O valor de retorno é a distância representada por um valor de ponto flutuante.
Imediatamente, é possível escrever um rascunho da função:
def distance(x1, y1, x2, y2):
return 0.0
Claro que esta versão não calcula distâncias; sempre retorna zero. Mas está sintaticamente correta, e pode ser executada, o que significa que você pode testá-la antes de torná-la mais complicada.
Para testar a nova função, chame-a com argumentos de amostra:
>>> distance(1, 2, 4, 6)
0.0
Escolhi esses valores para que a distância horizontal seja 3 e a distância vertical, 4; assim, o resultado final é 5, a hipotenusa de um triângulo 3-4-5. Ao testar uma função, é útil saber a resposta certa.
Neste ponto confirmamos que a função está sintaticamente correta, e podemos começar a acrescentar código ao corpo. Um próximo passo razoável é encontrar as diferenças x2 − x1 e y2 − y1. A próxima versão guarda esses valores em variáveis temporárias e os exibe:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
print('dx is', dx)
print('dy is', dy)
return 0.0
Se a função estiver funcionando, deve exibir dx is 3 e dy is 4. Nesse caso sabemos que a função está recebendo os argumentos corretos e executando o primeiro cálculo acertadamente. Se não, há poucas linhas para verificar.
Depois calculamos a soma dos quadrados de dx e dy:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
print('dsquared is: ', dsquared)
return 0.0
Nesta etapa você executaria o programa mais uma vez e verificaria a saída (que deve ser 25). Finalmente, pode usar math.sqrt para calcular e devolver o resultado:
def distance(x1, y1, x2, y2):
dx = x2 - x1
dy = y2 - y1
dsquared = dx**2 + dy**2
result = math.sqrt(dsquared)
return result
Se funcionar corretamente, pronto. Senão, uma ideia é exibir o valor result antes da instrução de retorno.
A versão final da função não exibe nada ao ser executada; apenas retorna um valor. As instruções print que escrevemos são úteis para depuração, mas assim que conferir se a função está funcionando você deve retirá-las. Códigos desse tipo são chamados de scaffolding (andaime) porque são úteis para construir o programa, mas não são parte do produto final.
Ao começar, você deveria acrescentar apenas uma linha ou duas de código de cada vez. Conforme adquira mais experiência, poderá escrever e depurar parcelas maiores. De qualquer forma, o desenvolvimento incremental pode economizar muito tempo de depuração.
Os principais aspectos do processo são:
-
Comece com um programa que funcione e faça pequenas alterações incrementais. Se houver um erro em qualquer ponto, será bem mais fácil encontrá-lo.
-
Use variáveis para guardar valores intermediários, assim poderá exibi-los e verificá-los.
-
Uma vez que o programa esteja funcionando, você pode querer remover uma parte do scaffolding ou consolidar várias instruções em expressões compostas, mas apenas se isso não tornar o programa difícil de ler.
Como exercício, use o desenvolvimento incremental para escrever uma função chamada hypotenuse, que devolva o comprimento da hipotenusa de um triângulo retângulo dados os comprimentos dos outros dois lados como argumentos. Registre cada etapa do processo de desenvolvimento no decorrer do processo.
6.3 - Composição
Como você já deveria esperar a essa altura, é possível chamar uma função de dentro de outra. Como exemplo, escreveremos uma função que recebe dois pontos, o centro do círculo e um ponto no perímetro, para calcular a área do círculo.
Suponha que o ponto do centro seja guardado nas variáveis xc e yc e o ponto de perímetro está em xp e yp. O primeiro passo deve ser encontrar o raio do círculo, que é a distância entre os dois pontos. Acabamos de escrever uma função, distance, que faz isto:
radius = distance(xc, yc, xp, yp)
O próximo passo deve ser encontrar a área de um círculo com aquele raio; acabamos de escrever isso também:
result = area(radius)
Encapsulando esses passos em uma função, temos:
def circle_area(xc, yc, xp, yp):
radius = distance(xc, yc, xp, yp)
result = area(radius)
return result
As variáveis temporárias radius e result são úteis para desenvolvimento e depuração, e uma vez que o programa esteja funcionando podemos torná-lo mais conciso compondo chamadas de função:
def circle_area(xc, yc, xp, yp):
return area(distance(xc, yc, xp, yp))
6.4 - Funções booleanas
As funções podem retornar booleans, o que pode ser conveniente para esconder testes complicados dentro de funções. Por exemplo:
def is_divisible(x, y):
if x % y == 0:
return True
else:
return False
É comum dar nomes de funções booleanas que pareçam perguntas de sim ou não; is_divisible retorna True ou False para indicar se x é divisível por y.
Aqui está um exemplo:
>>> is_divisible(6, 4)
False
>>> is_divisible(6, 3)
True
O resultado do operador == é um booleano, então podemos escrever a função de forma mais concisa, retornando-o diretamente:
def is_divisible(x, y):
return x % y == 0
As funções booleanas muitas vezes são usadas em instruções condicionais:
if is_divisible(x, y):
print('x is divisible by y')
Pode ser tentador escrever algo assim:
if is_divisible(x, y) == True:
print('x is divisible by y')
Mas a comparação extra é desnecessária.
Como um exercício, escreva uma função is_between(x, y, z) que retorne True, se x ≤ y ≤ z, ou False, se não for o caso.
6.5 - Mais recursividade
Cobrimos apenas um pequeno subconjunto do Python, mas talvez seja bom você saber que este subconjunto é uma linguagem de programação completa, ou seja, qualquer coisa que possa ser calculada pode ser expressa nesta linguagem. Qualquer programa que já foi escrito pode ser reescrito apenas com os recursos da linguagem que você aprendeu até agora (na verdade, seria preciso alguns comandos para dispositivos de controle como mouse, discos etc., mas isso é tudo).
Comprovar esta declaração é um exercício nada trivial realizado pela primeira vez por Alan Turing, um dos primeiros cientistas da computação (alguns diriam que ele foi matemático, mas muitos dos primeiros cientistas da computação começaram como matemáticos). Assim, é conhecida como a Tese de Turing. Para uma exposição mais completa (e exata) da Tese de Turing, recomendo o livro de Michael Sipser, Introduction to the Theory of Computation (Introdução à teoria da computação, Course Technology, 2012).
Para dar uma ideia do que podemos fazer com as ferramentas que aprendeu até agora, avaliaremos algumas funções matemáticas definidas recursivamente. Uma definição recursiva é semelhante a uma definição circular, no sentido de que a definição contém uma referência à coisa que é definida. Uma definição realmente circular não é muito útil:
vorpal
Adjetivo usado para descrever algo que é vorpal.
Ver uma definição assim no dicionário pode ser irritante. Por outro lado, se procurar a definição da função de fatorial, denotada pelo símbolo !, você pode encontrar algo assim:
0! = 1
n! = n·(n − 1)!
Esta definição diz que o fatorial de 0 é 1, e o fatorial de qualquer outro valor, n, é n multiplicado pelo fatorial de n-1.
Então 3! é 3 vezes 2!, que é 2 vezes 1!, que é 1 vez 0!. Juntando tudo, 3! é igual a 3 vezes 2 vezes 1 vezes 1, que é 6.
Se puder escrever uma definição recursiva de algo, você poderá escrever um programa em Python que a avalie. O primeiro passo deve ser decidir quais parâmetros ela deve ter. Neste caso, deve estar claro que factorial recebe um número inteiro:
def factorial(n):
Se o argumento for 0, tudo que temos de fazer é retornar 1:
def factorial(n):
if n == 0:
return 1
Senão, e aí é que fica interessante, temos que fazer uma chamada recursiva para encontrar o fatorial de n-1 e então multiplicá-lo por n:
def factorial(n):
if n == 0:
return 1
else:
recurse = factorial(n-1)
result = n * recurse
return result
O fluxo de execução deste programa é semelhante ao fluxo de countdown em “Recursividade”, na página 81. Se chamarmos factorial com o valor 3:
Como 3 não é 0, tomamos o segundo ramo e calculamos o fatorial de n-1...
Como 2 não é 0, tomamos o segundo ramo e calculamos o fatorial de n-1...
Como 1 não é 0, tomamos o segundo ramo e calculamos o fatorial de n-1...
Como 0 é igual a 0, tomamos o primeiro ramo e devolvemos 1 sem fazer mais chamadas recursivas.
O valor de retorno, 1, é multiplicado por n, que é 1, e o resultado é devolvido.
O valor de retorno, 1, é multiplicado por n, que é 2, e o resultado é devolvido.
O valor devolvido (2) é multiplicado por n, que é 3, e o resultado, 6, torna-se o valor devolvido pela chamada de função que começou o processo inteiro.
A Figura 6.1 mostra como é o diagrama da pilha para esta sequência de chamadas de função.
 .
.
Figura 6.1 – Diagrama da pilha para factorial.
Os valores devolvidos são mostrados ao serem passados de volta até o alto da pilha. Em cada frame, o valor devolvido é o valor de result, que é o produto de n e recurse.
No último frame, as variáveis locais recurse e result não existem, porque o ramo que os cria não é executado.
6.6 - Salto de fé
Seguir o fluxo da execução é uma forma de ler programas, mas poderá ser trabalhoso demais. Uma alternativa é o que chamo de “salto de fé” (leap of faith). Ao chegar a uma chamada de função, em vez de seguir o fluxo de execução suponha que a função esteja funcionando corretamente e que está retornando o resultado certo.
Na verdade, você já está praticando este salto de fé quando usa funções integradas. Quando chama math.cos ou math.exp, você não examina o corpo dessas funções. Apenas supõe que funcionem porque as pessoas que as escreveram eram bons programadores.
O mesmo acontece ao chamar uma das suas próprias funções. Por exemplo, em “Funções booleanas”, na página 97, escrevemos uma função chamada is_divisible que determina se um número é divisível por outro. Uma vez que estejamos convencidos de que esta função está correta – examinando o código e testando – podemos usar a função sem ver o corpo novamente.
O mesmo é verdade para programas recursivos. Quando chega à chamada recursiva, em vez de seguir o fluxo de execução, você deveria supor que a chamada recursiva funcione (devolva o resultado correto) e então perguntar-se: “Supondo que eu possa encontrar o fatorial de n-1, posso calcular o fatorial de n?”. É claro que pode, multiplicando por n.
Naturalmente, é um pouco estranho supor que a função funcione corretamente quando ainda não terminou de escrevê-la, mas é por isso que se chama um salto de fé!
6.7 - Mais um exemplo
Depois do factorial, o exemplo mais comum de uma função matemática definida recursivamente é fibonacci, que tem a seguinte definição (ver http://en.wikipedia.org/wiki/Fibonacci_number):
fibonacci(0) = 0
fibonacci(1) = 1
fibonacci(n) = fibonacci(n − 1) + fibonacci(n − 2)
Traduzida para Python, ela fica assim:
def fibonacci (n):
if n == 0:
return 0
elif n == 1:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)
Se tentar seguir o fluxo de execução aqui, até para valores razoavelmente pequenos de n, sua cabeça explode. Porém, seguindo o salto de fé, supondo que as duas chamadas recursivas funcionem corretamente, então é claro que vai receber o resultado correto adicionando-as juntas.
6.8 - Verificação de tipos
O que acontece se chamarmos factorial e usarmos 1.5 como argumento?
>>> factorial(1.5)
RuntimeError: Maximum recursion depth exceeded
Parece uma recursividade infinita. No entanto, por que isso acontece? A função tem um caso-base – quando n == 0. Mas se n não é um número inteiro, podemos perder o caso-base e recorrer para sempre.
Na primeira chamada recursiva, o valor de n é 0.5. No seguinte, é -0.5. Daí, torna-se menor (mais negativo), mas nunca será 0.
Temos duas escolhas. Podemos tentar generalizar a função factorial para trabalhar com números de ponto flutuante, ou podemos fazer factorial controlar o tipo de argumento que recebe. A primeira opção chama-se função gamma e está um pouco além do alcance deste livro. Então usaremos a segunda opção.
Podemos usar a função integrada isinstance para verificar o tipo de argumento. E vamos aproveitar para verificar também se o argumento é positivo:
def factorial (n):
if not isinstance(n, int):
print('Factorial is only defined for integers.')
return None
elif n < 0:
print('Factorial is not defined for negative integers.')
return None
elif n == 0:
return 1
else:
return n * factorial(n-1)
O primeiro caso-base lida com números não inteiros; o segundo, com números inteiros negativos. Em ambos os casos o programa exibe uma mensagem de erro e retorna None para indicar que algo deu errado:
>>> factorial('fred')
Factorial is only defined for integers.
None
>>> factorial(-2)
Factorial is not defined for negative integers.
None
Se passarmos por ambas as verificações, sabemos que n é positivo ou zero, então podemos comprovar que a recursividade termina.
Esse programa demonstra um padrão às vezes chamado de guardião. As duas primeiras condicionais atuam como guardiãs, protegendo o código que segue de valores que poderiam causar um erro. As guardiãs permitem comprovar a correção do código.
Na “Busca reversa”, na página 165, veremos uma alternativa mais flexível para a exibição de uma mensagem de erro: o levantamento de exceções.
6.9 - Depuração
Quebrar um grande programa em funções menores cria controles naturais da depuração. Se uma função não estiver funcionando, há três possibilidades a considerar:
-
Há algo errado com os argumentos que a função está recebendo; uma precondição está sendo violada.
-
Há algo errado com a função; uma pós-condição foi violada.
-
Há algo errado com o valor de retorno ou a forma na qual está sendo usado.
Para excluir a primeira possibilidade, você pode acrescentar uma instrução print no início da função e exibir os valores dos parâmetros (e talvez os seus tipos). Ou escrever código que verifique as precondições explicitamente.
Se os parâmetros parecerem bons, acrescente uma instrução print antes de cada instrução return e exiba o valor de retorno. Se possível, verifique o resultado à mão. Uma possibilidade é chamar a função com valores facilitem a verificação do resultado (como no “Desenvolvimento incremental”, da página 94).
Se a função parecer funcionar, veja a chamada da função para ter certeza de que o valor de retorno está sendo usado corretamente (ou se está sendo usado mesmo!).
Acrescentar instruções de exibição no começo e no fim de uma função pode ajudar a tornar o fluxo de execução mais visível. Por exemplo, aqui está uma versão de factorial com instruções de exibição:
def factorial(n):
space = ' ' * (4 * n)
print(space, 'factorial', n)
if n == 0:
print(space, 'returning 1')
return 1
else:
recurse = factorial(n-1)
result = n * recurse
print(space, 'returning', result)
return result
space é uma string de caracteres especiais que controla a endentação da saída. Aqui está o resultado de factorial(4):
factorial 4
factorial 3
factorial 2
factorial 1
factorial 0
returning 1
returning 1
returning 2
returning 6
returning 24
Se o fluxo de execução parecer confuso a você, este tipo de saída pode ser útil. Leva um tempo para desenvolver um scaffolding eficaz, mas um pouco dele pode economizar muita depuração.
6.10 - Glossário
variável temporária
Uma variável usada para guardar um valor intermediário em um cálculo complexo.
código morto
A parte de um programa que nunca pode ser executada, muitas vezes porque aparece depois de uma instrução return.
desenvolvimento incremental
Um plano de desenvolvimento de programa para evitar a depuração, que acrescenta e testa poucas linhas de código de cada vez.
scaffolding (andaime)
O código que se usa durante o desenvolvimento de programa, mas que não faz parte da versão final.
guardião
Um padrão de programação que usa uma instrução condicional para verificar e lidar com circunstâncias que possam causar erros.
6.11 - Exercícios
Exercício 6.1
Desenhe um diagrama da pilha do seguinte programa. O que o programa exibe?
def b(z):
prod = a(z, z)
print(z, prod)
return prod
def a(x, y):
x = x + 1
return x * y
def c(x, y, z):
total = x + y + z
square = b(total)**2
return square
x = 1
y = x + 1
print(c(x, y+3, x+y))
Exercício 6.2
A função de Ackermann, A(m, n), é definida assim:
 .
.
Veja http://en.wikipedia.org/wiki/Ackermann_function. Escreva uma função denominada ack que avalie a função de Ackermann. Use a sua função para avaliar ack(3, 4), cujo resultado deve ser 125. O que acontece para valores maiores de m e n?
Solução: http://thinkpython2.com/code/ackermann.py.
Exercício 6.3
Um palíndromo é uma palavra que se soletra da mesma forma nos dois sentidos, como “osso” e “reviver”. Recursivamente, uma palavra é um palíndromo se a primeira e última letras forem iguais e o meio for um palíndromo.
As funções seguintes recebem uma string como argumento e retornam as letras iniciais, finais e do meio das palavras:
def first(word):
return word[0]
def last(word):
return word[-1]
def middle(word):
return word[1:-1]
Veremos como funcionam no Capítulo 8.
-
Digite essas funções em um arquivo chamado palindrome.py e teste-as. O que acontece se chamar middle com uma string de duas letras? Uma letra? E se a string estiver vazia, escrita com
''e não contiver nenhuma letra? -
Escreva uma função chamada
is_palindromeque receba uma string como argumento e retorne True se for um palíndromo e False se não for. Lembre-se de que você pode usar a função integrada len para verificar o comprimento de uma string.
Solução: http://thinkpython2.com/code/palindrome_soln.py.
Exercício 6.4
Um número a é uma potência de b se for divisível por b e a/b for uma potência de b. Escreva uma função chamada is_power que receba os parâmetros a e b e retorne True se a for uma potência de b. Dica: pense no caso-base.
Exercício 6.5
O maior divisor comum (MDC, ou GCD em inglês) de a e b é o maior número que divide ambos sem sobrar resto.
Um modo de encontrar o MDC de dois números é observar qual é o resto r quando a é dividido por b, verificando que gcd(a, b) = gcd(b, r). Como caso-base, podemos usar gcd(a, 0) = a.
Escreva uma função chamada gcd que receba os parâmetros a e b e devolva o maior divisor comum.
Crédito: Este exercício é baseado em um exemplo do livro de Abelson e Sussman, Structure and Interpretation of Computer Programs (Estrutura e interpretação de programas de computador, MIT Press, 1996).
Capítulo 7: Iteração
Este capítulo é sobre a iteração, a capacidade de executar um bloco de instruções repetidamente. Vimos um tipo de iteração, usando a recursividade, em “Recursividade”, na página 81. Vimos outro tipo, usando um loop for, em “Repetição simples”, na página 65. Neste capítulo veremos ainda outro tipo, usando a instrução while. Porém, primeiro quero falar um pouco mais sobre a atribuição de variáveis.
7.1 - Reatribuição
Pode ser que você já tenha descoberto que é permitido fazer mais de uma atribuição para a mesma variável. Uma nova atribuição faz uma variável existente referir-se a um novo valor (e deixar de referir-se ao valor anterior).
>>> x = 5
>>> x
5
>>> x = 7
>>> x
7
A primeira vez que exibimos x, seu valor é 5; na segunda vez, seu valor é 7.
A Figura 7.1 mostra que a reatribuição parece um diagrama de estado.
Neste ponto quero tratar de uma fonte comum de confusão. Como o Python usa o sinal de igual (=) para atribuição, é tentador interpretar uma afirmação como a = b como uma proposição matemática de igualdade; isto é, a declaração de que a e b são iguais. Mas esta é uma interpretação equivocada.
Em primeiro lugar, a igualdade é uma relação simétrica e a atribuição não é. Por exemplo, na matemática, se a=7 então 7=a. Mas no Python, a instrução a = 7 é legal e 7 = a não é.
Além disso, na matemática, uma proposição de igualdade é verdadeira ou falsa para sempre. Se a=b agora, então a sempre será igual a b. No Python, uma instrução de atribuição pode tornar duas variáveis iguais, mas elas não precisam se manter assim:
>>> a = 5
>>> b = a # a e b agora são iguais
>>> a = 3 # a e b não são mais iguais
>>> b
5
A terceira linha modifica o valor de a, mas não muda o valor de b, então elas já não são iguais.
A reatribuição de variáveis muitas vezes é útil, mas você deve usá-la com prudência. Se os valores das variáveis mudarem frequentemente, isso pode dificultar a leitura e depuração do código.
Figura 7.1 – Diagrama de estado.
 .
.
Figura 7.1 – Diagrama de estado da variável x.
7.2 - Atualização de variáveis
Um tipo comum de reatribuição é uma atualização, onde o novo valor da variável depende do velho.
>>> x = x + 1
Isso significa “pegue o valor atual de x, acrescente um, e então atualize x para o novo valor”.
Se você tentar atualizar uma variável que não existe, recebe um erro porque o Python avalia o lado direito antes de atribuir um valor a x:
>>> x = x + 1
NameError: name 'x' is not defined
Antes de poder atualizar uma variável é preciso inicializá-la, normalmente com uma atribuição simples:
>>> x = 0
>>> x = x + 1
Atualizar uma variável acrescentando 1 chama-se incremento; subtrair 1 chama-se decremento.
7.3 - Instrução while
Os computadores muitas vezes são usados para automatizar tarefas repetitivas. A repetição de tarefas idênticas ou semelhantes sem fazer erros é algo que os computadores fazem bem e as pessoas não. Em um programa de computador, a repetição também é chamada de iteração.
Já vimos duas funções, countdown e print_n, que se repetem usando recursividade. Como a iteração é bem comum, o Python fornece recursos de linguagem para facilitá-la. Um deles é a instrução for que vimos em “Repetição simples”, na página 65. Voltaremos a isso mais adiante.
Outra é a instrução while. Aqui está uma versão de countdown que usa a instrução while:
def countdown(n):
while n > 0:
print(n)
n = n - 1
print('Blastoff!')
Você até pode ler a instrução while como se fosse uma tradução do inglês. Significa “Enquanto n for maior que 0, mostre o valor de n e então decremente n. Quando chegar a 0, mostre a palavra Blastoff!”
Mais formalmente, aqui está o fluxo de execução para uma instrução while:
-
Determine se a condição é verdadeira ou falsa.
-
Se for falsa, saia da instrução while e continue a execução da próxima instrução.
-
Se a condição for verdadeira, execute o corpo e então volte ao passo 1.
Este tipo de fluxo chama-se loop (laço), porque o terceiro passo faz um loop de volta ao topo.
O corpo do loop deve mudar o valor de uma ou mais variáveis para que, a certa altura, a condição fique falsa e o loop termine. Senão o loop vai se repetir para sempre, o que é chamado de loop infinito. Uma fonte infindável de divertimento para cientistas da computação é a observação das instruções no xampu, “Faça espuma, enxágue, repita”, que são parte de um loop infinito.
No caso de countdown, podemos provar que o loop termina: se n for zero ou negativo, o loop nunca é executado. Senão, n fica cada vez menor ao passar pelo loop, até eventualmente chegar a 0.
Para alguns outros loops, não é tão fácil perceber isso. Por exemplo:
def sequence(n):
while n != 1:
print(n)
if n % 2 == 0: # n é par
n = n / 2
else: # n é ímpar
n = n * 3 + 1
A condição deste loop é n != 1, então o loop continuará até que n seja 1, o que torna a condição falsa.
Cada vez que passa pelo loop, o programa produz o valor de n e então verifica se é par ou ímpar. Se for par, n é dividido por 2. Se for ímpar, o valor de n é substituído por n * 3 + 1. Por exemplo, se o argumento passado a sequence for 3, os valores resultantes de n são 3, 10, 5, 16, 8, 4, 2, 1.
Como n às vezes aumenta e às vezes diminui, não há nenhuma prova óbvia de que n chegará eventualmente a 1, ou que o programa terminará. Para alguns valores de n, podemos provar o término. Por exemplo, se o valor inicial for uma potência de dois, n será par cada vez que passar pelo loop até que chegue a 1. O exemplo anterior termina com uma sequência assim, que inicia com 16.
A questão difícil é se podemos provar que este programa termina para todos os valores positivos de n. Por enquanto, ninguém foi capaz de comprovar ou refutar isso! (Veja http://en.wikipedia.org/wiki/Collatz_conjecture.)
Como um exercício, reescreva a função print_n de “Recursividade”, na página 81, usando a iteração em vez da recursividade.
7.4 - break
Às vezes você não sabe que está na hora de terminar um loop até que já esteja na metade do corpo. Neste caso pode usar a instrução break para sair do loop.
Por exemplo, suponha que você quer receber uma entrada do usuário até que este digite done. Você pode escrever:
while True:
line = input('> ')
if line == 'done':
break
print(line)
print('Done!')
A condição do loop é True, que sempre é verdade, então o loop roda até que chegue à instrução de interrupção.
Cada vez que passa pelo loop, o programa apresenta ao usuário um colchete angular. Se o usuário digitar done, a instrução break sai do loop. Senão, o programa ecoa o que quer que o usuário digite e volta ao topo do loop. Aqui está uma amostra de execução:
> not done
not done
> done
Done!
Esta forma de escrever loops while é comum porque podemos verificar a condição em qualquer lugar do loop (não somente no topo) e podemos exprimir a condição de parada afirmativamente (“pare quando isto acontecer”) em vez de negativamente (“continue a seguir até que isto aconteça”).
7.5 - Raízes quadradas
Loops muitas vezes são usados em programas que calculam resultados numéricos, começando com uma resposta aproximada e melhorando-a iterativamente.
Por exemplo, uma forma de calcular raízes quadradas é o método de Newton. Suponha que você queira saber a raiz quadrada de a. Se começar com quase qualquer estimativa, x, é possível calcular uma estimativa melhor com a seguinte fórmula:
 .
.
Por exemplo, se a for 4 e x for 3:
>>> a = 4
>>> x = 3
>>> y = (x + a/x) / 2
>>> y
2.16666666667
O resultado é mais próximo à resposta correta ( . = 2). Se repetirmos o processo com a nova estimativa, chegamos ainda mais perto:
. = 2). Se repetirmos o processo com a nova estimativa, chegamos ainda mais perto:
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00641025641
Depois de algumas atualizações, a estimativa é quase exata:
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00001024003
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00000000003
Em geral, não sabemos com antecedência quantos passos são necessários para chegar à resposta correta, mas sabemos quando chegamos lá porque a estimativa para de mudar:
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.0
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.0
Quando y == x, podemos parar. Aqui está um loop que começa com uma estimativa inicial, x, e a melhora até que deixe de mudar:
while True:
print(x)
y = (x + a/x) / 2
if y == x:
break
x = y
Para a maior parte de valores de a funciona bem, mas pode ser perigoso testar a igualdade de um float. Os valores de ponto flutuante são aproximadamente corretos: a maioria dos números racionais, como 1/3, e números irracionais, como  ., não podem ser representados exatamente com um float.
., não podem ser representados exatamente com um float.
Em vez de verificar se x e y são exatamente iguais, é mais seguro usar a função integrada abs para calcular o valor absoluto ou magnitude da diferença entre eles:
if abs(y-x) < epsilon:
break
Onde epsilon tem um valor como 0.0000001, que determina a proximidade desejada entre x e y.
7.6 - Algoritmos
O método de Newton é um exemplo de um algoritmo: um processo mecânico para resolver uma categoria de problemas (neste caso, calcular raízes quadradas).
Para entender o que é um algoritmo, pode ser útil começar com algo que não é um algoritmo. Quando aprendeu a multiplicar números de um dígito, você provavelmente memorizou a tabuada. Ou seja, você memorizou 100 soluções específicas. Este tipo de conhecimento não é algorítmico.
No entanto, se você foi “preguiçoso”, poderia ter aprendido alguns truques. Por exemplo, para encontrar o produto de n e 9, pode escrever n-1 como o primeiro dígito e 10-n como o segundo dígito. Este truque é uma solução geral para multiplicar qualquer número de dígito único por 9. Isto é um algoritmo!
De forma semelhante, as técnicas que aprendeu, como o transporte na adição, o empréstimo na subtração e a divisão longa são todos algoritmos. Uma das características de algoritmos é que eles não exigem inteligência para serem executados. São processos mecânicos, nos quais cada passo segue a partir do último, de acordo com um conjunto de regras simples.
A execução de algoritmos é maçante, mas projetá-los é interessante, intelectualmente desafiador e uma parte central da Ciência da Computação.
Algumas coisas que as pessoas fazem naturalmente, sem dificuldade ou pensamento consciente, são as mais difíceis para exprimir algoritmicamente. A compreensão de linguagem natural é um bom exemplo. Todos nós o fazemos, mas por enquanto ninguém foi capaz de explicar como o fazemos, pelo menos não na forma de um algoritmo.
7.7 - Depuração
Ao começar a escrever programas maiores, pode ser que você passe mais tempo depurando. Mais código significa mais possibilidades fazer erros e mais lugares para esconder defeitos.
Uma forma de cortar o tempo de depuração é “depurar por bisseção”. Por exemplo, se há 100 linhas no seu programa e você as verifica uma a uma, seriam 100 passos a tomar.
Em vez disso, tente quebrar o problema pela metade. Olhe para o meio do programa, ou perto disso, para um valor intermediário que possa verificar. Acrescente uma instrução print (ou outra coisa que tenha um efeito verificável) e execute o programa.
Se a verificação do ponto central for incorreta, deve haver um problema na primeira metade do programa. Se for correta, o problema está na segunda metade.
Cada vez que executar uma verificação assim, divida ao meio o número de linhas a serem verificadas. Depois de seis passos (que é menos de 100), você teria menos de uma ou duas linhas do código para verificar, pelo menos em teoria.
Na prática, nem sempre é claro o que representa o “meio do programa” e nem sempre é possível verificá-lo. Não faz sentido contar linhas e encontrar o ponto central exato. Em vez disso, pense em lugares no programa onde poderia haver erros e lugares onde é fácil inserir um ponto de verificação. Então escolha um lugar onde as possibilidades são basicamente as mesmas de que o defeito esteja antes ou depois da verificação.
7.8 - Glossário
reatribuição
Atribuir um novo valor a uma variável que já existe.
atualização
Uma atribuição onde o novo valor da variável dependa do velho.
inicialização
Uma atribuição que dá um valor inicial a uma variável que será atualizada.
incremento
Uma atualização que aumenta o valor de uma variável (normalmente por uma unidade).
decremento
Uma atualização que reduz o valor de uma variável.
iteração
Execução repetida de um grupo de instruções, usando uma chamada da função recursiva ou um loop.
loop infinito
Um loop no qual a condição de término nunca é satisfeita.
algoritmo
Um processo geral para resolver uma categoria de problemas.
7.9 - Exercícios
Exercício 7.1
Copie o loop de “Raízes quadradas”, na página 111, e encapsule-o em uma função chamada mysqrt que receba a como parâmetro, escolha um valor razoável de x e devolva uma estimativa da raiz quadrada de a.
Para testar, escreva uma função denominada test_square_root, que exibe uma tabela como esta:
a mysqrt(a) math.sqrt(a) diff
- --------- ------------ ----
1.0 1.0 1.0 0.0
2.0 1.41421356237 1.41421356237 2.22044604925e-16
3.0 1.73205080757 1.73205080757 0.0
4.0 2.0 2.0 0.0
5.0 2.2360679775 2.2360679775 0.0
6.0 2.44948974278 2.44948974278 0.0
7.0 2.64575131106 2.64575131106 0.0
8.0 2.82842712475 2.82842712475 4.4408920985e-16
9.0 3.0 3.0 0.0
A primeira coluna é um número, a; a segunda coluna é a raiz quadrada de a calculada com mysqrt; a terceira coluna é a raiz quadrada calculada por math.sqrt; a quarta coluna é o valor absoluto da diferença entre as duas estimativas.
Exercício 7.2
A função integrada eval toma uma string e a avalia, usando o interpretador do Python. Por exemplo:
>>> eval('1 + 2 * 3')
7
>>> import math
>>> eval('math.sqrt(5)')
2.2360679774997898
>>> eval('type(math.pi)')
<class 'float'>
Escreva uma função chamada eval_loop que iterativamente peça uma entrada ao usuário, a avalie usando eval e exiba o resultado.
Ela deve continuar até que o usuário digite done; então deverá exibir o valor da última expressão avaliada.
Exercício 7.3
O matemático Srinivasa Ramanujan encontrou uma série infinita que pode ser usada para gerar uma aproximação numérica de 1/π:
 .
.
Escreva uma função chamada estimate_pi que use esta fórmula para computar e devolver uma estimativa de π. Você deve usar o loop while para calcular os termos da adição até que o último termo seja menor que 1e-15 (que é a notação do Python para 10 ** 15). Você pode verificar o resultado comparando-o com math.pi.
Capítulo 8: Strings
Strings não são como números inteiros, de ponto flutuante ou booleanos. Uma string é uma sequência, ou seja, uma coleção ordenada de outros valores. Neste capítulo você verá como acessar os caracteres que compõem uma string e aprenderá alguns métodos que as strings oferecem.
8.1 - Uma string é uma sequência
Uma string é uma sequência de caracteres. Você pode acessar um caractere de cada vez com o operador de colchete:
>>> fruit = 'banana'
>>> letter = fruit[1]
A segunda instrução seleciona o caractere número 1 de fruit e o atribui a letter.
A expressão entre colchetes chama-se índice. O índice aponta qual caractere da sequência você quer (daí o nome).
Mas pode ser que você não obtenha o que espera:
>>> letter
'a'
Para a maior parte das pessoas, a primeira letra de 'banana' é b, não a. Mas para os cientistas da computação, o índice é uma referência do começo da string, e a referência da primeira letra é zero.
>>> letter = fruit[0]
>>> letter
'b'
Então b é a 0ª (“zerésima”) letra de 'banana', a é a 1ª (primeira) letra e n é a 2ª (segunda) letra.
Você pode usar uma expressão que contenha variáveis e operadores como índice:
>>> i = 1
>>> fruit[i]
'a'
>>> fruit[i+1]
'n'
Porém, o valor do índice tem que ser um número inteiro. Se não for, é isso que aparece:
>>> letter = fruit[1.5]
TypeError: string indices must be integers
8.2 - len
len é uma função integrada que devolve o número de caracteres em uma string:
>>> fruit = 'banana'
>>> len(fruit)
6
Para obter a última letra de uma string, pode parecer uma boa ideia tentar algo assim:
>>> length = len(fruit)
>>> last = fruit[length]
IndexError: string index out of range
A razão de haver um IndexError aqui é que não há nenhuma letra em 'banana' com o índice 6. Como a contagem inicia no zero, as seis letras são numeradas de 0 a 5. Para obter o último caractere, você deve subtrair 1 de length:
>>> last = fruit[length-1]
>>> last
'a'
Ou você pode usar índices negativos, que contam de trás para a frente a partir do fim da string. A expressão fruit[-1] apresenta a última letra, fruit[-2] apresenta a segunda letra de trás para a frente, e assim por diante.
8.3 - Travessia com loop for
Muitos cálculos implicam o processamento de um caractere por vez em uma string. Muitas vezes começam no início, selecionam um caractere por vez, fazem algo e continuam até o fim. Este modelo do processamento chama-se travessia. Um modo de escrever uma travessia é com o loop while:
index = 0
while index < len(fruit):
letter = fruit[index]
print(letter)
index = index + 1
Este loop atravessa a string e exibe cada letra sozinha em uma linha. A condição do loop é index <len (fruit), então quando index é igual ao comprimento da string, a condição é falsa e o corpo do loop não é mais executado. O último caractere acessado é aquele com o índice len (fruit)-1, que é o último caractere na string.
Como exercício, escreva uma função que receba uma string como argumento e exiba as letras de trás para a frente, uma por linha.
Outra forma de escrever uma travessia é com um loop for:
for letter in fruit:
print(letter)
Cada vez que o programa passar pelo loop, o caractere seguinte na string é atribuído à variável letter. O loop continua até que não sobre nenhum caractere.
O próximo exemplo mostra como usar a concatenação (adição de strings) e um loop for para gerar uma série abecedária (isto é, em ordem alfabética). No livro de Robert McCloskey, Make Way for Ducklings (Abram caminho para os patinhos), os nomes dos patinhos são Jack, Kack, Lack, Mack, Nack, Ouack, Pack e Quack. Este loop produz estes nomes em ordem:
prefixes = 'JKLMNOPQ'
suffix = 'ack'
for letter in prefixes:
print(letter + suffix)
A saída é:
Jack
Kack
Lack
Mack
Nack
Oack
Pack
Qack
Claro que não está exatamente certo porque “Ouack” e “Quack” foram mal soletrados. Como exercício, altere o programa para corrigir este erro.
8.4 - Fatiamento de strings
Um segmento de uma string é chamado de fatia. Selecionar uma fatia é como selecionar um caractere:
>>> s = 'Monty Python'
>>> s[0:5]
'Monty'
>>> s[6:12]
'Python'
O operador [n:m] retorna a parte da string do “enésimo” caractere ao “emésimo” caractere, incluindo o primeiro, mas excluindo o último. Este comportamento é contraintuitivo, porém pode ajudar a imaginar os índices que indicam a parte entre os caracteres, como na Figura 8.1.
 .
.
Figura 8.1 – Índices de fatias.
Se você omitir o primeiro índice (antes dos dois pontos), a fatia começa no início da string. Se omitir o segundo índice, a fatia vai ao fim da string:
>>> fruit = 'banana'
>>> fruit[:3]
'ban'
>>> fruit[3:]
'ana'
Se o primeiro índice for maior ou igual ao segundo, o resultado é uma string vazia, representada por duas aspas:
>>> fruit = 'banana'
>>> fruit[3:3]
''
Uma string vazia não contém nenhum caractere e tem o comprimento 0, fora isso, é igual a qualquer outra string.
Continuando este exemplo, o que você acha que fruit[:] significa? Teste e veja.
8.5 - Strings são imutáveis
É tentador usar o operador [] no lado esquerdo de uma atribuição, com a intenção de alterar um caractere em uma string. Por exemplo:
>>> greeting = 'Hello, world!'
>>> greeting[0] = 'J'
TypeError: 'str' object does not support item assignment
O “objeto” neste caso é a string e o “item” é o caractere que você tentou atribuir. Por enquanto, um objeto é a mesma coisa que um valor, mas refinaremos esta definição mais adiante (Objetos e valores, no capítulo 10).
A razão do erro é que as strings são imutáveis, o que significa que você não pode alterar uma string existente. O melhor que você pode fazer é criar uma string que seja uma variação da original:
>>> greeting = 'Hello, world!'
>>> new_greeting = 'J' + greeting[1:]
>>> new_greeting
'Jello, world!'
Esse exemplo concatena uma nova primeira letra a uma fatia de greeting. Não tem efeito sobre a string original.
8.6 - Buscando
O que faz a seguinte função?
def find(word, letter):
index = 0
while index < len(word):
if word[index] == letter:
return index
index = index + 1
return-1
De certo modo, find é o inverso do operador []. Em vez de tomar um índice e extrair o caractere correspondente, ele toma um caractere e encontra o índice onde aquele caractere aparece. Se o caractere não for encontrado, a função retorna -1.
Esse é o primeiro exemplo que vimos de uma instrução return dentro de um loop. Se word[index] == letter, a função sai do loop e retorna imediatamente.
Se o caractere não aparecer na string, o programa sai do loop normalmente e devolve -1.
Este modelo de cálculo – atravessar uma sequência e retornar quando encontramos o que estamos procurando – chama-se busca.
Como exercício, altere find para que tenha um terceiro parâmetro: o índice em word onde deve começar a busca.
8.7 - Loop e contagem
O seguinte programa conta o número de vezes que a letra a aparece em uma string:
word = 'banana'
count = 0
for letter in word:
if letter == 'a':
count = count + 1
print(count)
Este programa demonstra outro padrão de computação chamado contador. A variável count é inicializada com 0 e então incrementada cada vez que um a é encontrado. Ao sair do loop, count contém o resultado – o número total de letras 'a'.
Como exercício, encapsule este código em uma função denominada count e generalize-o para que aceite a string e a letra como argumentos.
Então reescreva a função para que, em vez de atravessar a string, ela use a versão de três parâmetros do find da seção anterior.
8.8 - Métodos de strings
As strings oferecem métodos que executam várias operações úteis. Um método é semelhante a uma função – toma argumentos e devolve um valor –, mas a sintaxe é diferente. Por exemplo, o método upper recebe uma string e devolve uma nova string com todas as letras maiúsculas.
Em vez da sintaxe de função upper(word), ela usa a sintaxe de método word.upper():
>>> word = 'banana'
>>> new_word = word.upper()
>>> new_word
'BANANA'
Esta forma de notação de ponto especifica o nome do método, upper e o nome da string, word, à qual o método será aplicado. Os parênteses vazios indicam que este método não toma nenhum argumento.
Uma chamada de método denomina-se invocação; neste caso, diríamos que estamos invocando upper em word.
E, na verdade, há um método de string denominado find, que é notavelmente semelhante à função que escrevemos:
>>> word = 'banana'
>>> index = word.find('a')
>>> index
1
Neste exemplo, invocamos find em word e passamos a letra que estamos procurando como um parâmetro.
Na verdade, o método find é mais geral que a nossa função; ele pode encontrar substrings, não apenas caracteres:
>>> word.find('na')
2
Por padrão, find inicia no começo da string, mas pode receber um segundo argumento, o índice onde deve começar:
>>> word.find('na', 3)
4
Este é um exemplo de um argumento opcional. find também pode receber um terceiro argumento, o índice para onde deve parar:
>>> name = 'bob'
>>> name.find('b', 1, 2)
-1
Esta busca falha porque 'b' não aparece no intervalo do índice de 1 a 2, não incluindo 2. Fazer buscas até (mas não incluindo) o segundo índice torna find similar ao operador de fatiamento.
8.9 - Operador in
A palavra in é um operador booleano que recebe duas strings e retorna True se a primeira aparecer como uma substring da segunda:
>>> 'a' in 'banana'
True
>>> 'seed' in 'banana'
False
Por exemplo, a seguinte função imprime todas as letras de word1 que também aparecem em word2:
def in_both(word1, word2):
for letter in word1:
if letter in word2:
print(letter)
Com nomes de variáveis bem escolhidos, o Python às vezes pode ser lido como um texto em inglês. Você pode ler este loop, “para (cada) letra em (a primeira) palavra, se (a) letra (aparecer) em (a segunda) palavra, exiba (a) letra”.
Veja o que é apresentado ao se comparar maçãs e laranjas:
>>> in_both('apples', 'oranges')
a
e
s
8.10 - Comparação de strings
Os operadores relacionais funcionam em strings. Para ver se duas strings são iguais:
if word == 'banana':
print('All right, bananas.')
Outras operações relacionais são úteis para colocar palavras em ordem alfabética:
if word < 'banana':
print('Your word, ' + word + ', comes before banana.')
elif word > 'banana':
print('Your word, ' + word + ', comes after banana.')
else:
print('All right, bananas.')
O Python não lida com letras maiúsculas e minúsculas do mesmo jeito que as pessoas. Todas as letras maiúsculas vêm antes de todas as letras minúsculas, portanto:
Your word, Pineapple, comes before banana.
Uma forma comum de lidar com este problema é converter strings em um formato padrão, como letras minúsculas, antes de executar a comparação. Lembre-se disso caso tenha que se defender de um homem armado com um abacaxi.
8.11 - Depuração
Ao usar índices para atravessar os valores em uma sequência, é complicado acertar o começo e o fim da travessia. Aqui está uma função que supostamente compara duas palavras e retorna True se uma das palavras for o reverso da outra, mas contém dois erros:
def is_reverse(word1, word2):
if len(word1) != len(word2):
return False
i = 0
j = len(word2)
while j > 0:
if word1[i] != word2[j]:
return False
i = i+1
j = j-1
return True
A primeira instrução if verifica se as palavras têm o mesmo comprimento. Se não for o caso, podemos retornar False imediatamente. Do contrário, para o resto da função, podemos supor que as palavras tenham o mesmo comprimento. Este é um exemplo do modelo de guardião em “Verificação de tipos”, na página 101.
i e j são índices: i atravessa word1 para a frente, enquanto j atravessa word2 para trás. Se encontrarmos duas letras que não combinam, podemos retornar False imediatamente. Se terminarmos o loop inteiro e todas as letras corresponderem, retornamos True.
Se testarmos esta função com as palavras “pots” e “stop”, esperamos o valor de retorno True, mas recebemos um IndexError:
>>> is_reverse('pots', 'stop')
...
File "reverse.py", line 15, in is_reverse
if word1[i] != word2[j]:
IndexError: string index out of range
Para depurar este tipo de erro, minha primeira ação é exibir os valores dos índices imediatamente antes da linha onde o erro aparece.
while j > 0:
print(i, j) # exibir aqui
if word1[i] != word2[j]:
return False
i = i+1
j = j-1
Agora quando executo o programa novamente, recebo mais informação:
>>> is_reverse('pots', 'stop')
0 4
...
IndexError: string index out of range
Na primeira vez que o programa passar pelo loop, o valor de j é 4, que está fora do intervalo da string 'pots'. O índice do último caractere é 3, então o valor inicial de j deve ser len(word2)-1.
Se corrigir esse erro e executar o programa novamente, recebo:
>>> is_reverse('pots', 'stop')
0 3
1 2
2 1
True
Desta vez, recebemos a resposta certa, mas parece que o loop só foi executado três vezes, o que é suspeito. Para ter uma ideia melhor do que está acontecendo, é útil desenhar um diagrama de estado. Durante a primeira iteração, o frame de is_reverse é mostrado na Figura 8.2.
 .
.
8.2 – Diagrama de estado de is_reverse.
Tomei a liberdade de arrumar as variáveis no frame e acrescentei linhas pontilhadas para mostrar que os valores de i e j indicam caracteres em word1 e word2.
Começando com este diagrama, execute o programa em papel, alterando os valores de i e j durante cada iteração. Encontre e corrija o segundo erro desta função.
8.12 - Glossário
objeto
Algo a que uma variável pode se referir. Por enquanto, você pode usar “objeto” e “valor” de forma intercambiável.
sequência
Uma coleção ordenada de valores onde cada valor é identificado por um índice de número inteiro.
item
Um dos valores em uma sequência.
índice
Um valor inteiro usado para selecionar um item em uma sequência, como um caractere em uma string. No Python, os índices começam em 0.
fatia
Parte de uma string especificada por um intervalo de índices.
string vazia
Uma string sem caracteres e de comprimento 0, representada por duas aspas.
imutável
A propriedade de uma sequência cujos itens não podem ser alterados.
atravessar
Repetir os itens em uma sequência, executando uma operação semelhante em cada um.
busca
Um modelo de travessia que é interrompido quando encontra o que está procurando.
contador
Uma variável usada para contar algo, normalmente inicializada com zero e então incrementada.
invocação
Uma instrução que chama um método.
argumento opcional
Um argumento de função ou método que não é necessário.
8.13 - Exercícios
Exercício 8.1
Leia a documentação dos métodos de strings em http://docs.python.org/3/library/stdtypes.html#string-methods. Pode ser uma boa ideia experimentar alguns deles para entender como funcionam. strip e replace são especialmente úteis.
A documentação usa uma sintaxe que pode ser confusa. Por exemplo, em find(sub[, start[, end]]), os colchetes indicam argumentos opcionais. Então sub é exigido, mas start é opcional, e se você incluir start, então end é opcional.
Exercício 8.2
Há um método de string chamado count, que é semelhante à função em “Loop e contagem”, na página 123. Leia a documentação deste método e escreva uma invocação que conte o número de letras 'a' em 'banana'.
Exercício 8.3
Uma fatia de string pode receber um terceiro índice que especifique o “tamanho do passo”; isto é, o número de espaços entre caracteres sucessivos. Um tamanho de passo 2 significa tomar um caractere e outro não; 3 significa tomar um e dois não etc.
>>> fruit = 'banana'
>>> fruit[0:5:2]
'bnn'
Um tamanho de passo -1 atravessa a palavra de trás para a frente, então a fatia [::-1] gera uma string invertida.
Use isso para escrever uma versão de uma linha de is_palindrome do Exercício 6.3.
Exercício 8.4
As seguintes funções pretendem verificar se uma string contém alguma letra minúscula, mas algumas delas estão erradas. Para cada função, descreva o que ela faz (assumindo que o parâmetro seja uma string).
def any_lowercase1(s):
for c in s:
if c.islower():
return True
else:
return False
def any_lowercase2(s):
for c in s:
if 'c'.islower():
return 'True'
else:
return 'False'
def any_lowercase3(s):
for c in s:
flag = c.islower()
return flag
def any_lowercase4(s):
flag = False
for c in s:
flag = flag or c.islower()
return flag
def any_lowercase5(s):
for c in s:
if not c.islower():
return False
return True
Exercício 8.5
Uma cifra de César é uma forma fraca de criptografia que implica “rotacionar” cada letra por um número fixo de lugares. Rotacionar uma letra significa deslocá-lo pelo alfabeto, voltando ao início se for necessário, portanto ‘A’ rotacionado por 3 é ‘D’ e ‘Z’ rotacionado por 1 é ‘A’.
Para rotacionar uma palavra, faça cada letra se mover pela mesma quantidade de posições. Por exemplo, “cheer” rotacionado por 7 é “jolly” e “melon” rotacionado por -10 é “cubed”. No filme 2001: Uma odisseia no espaço, o computador da nave chama-se HAL, que é IBM rotacionado por -1.
Escreva uma função chamada rotate_word que receba uma string e um número inteiro como parâmetros, e retorne uma nova string que contém as letras da string original rotacionadas pelo número dado.
Você pode usar a função integrada ord, que converte um caractere em um código numérico e chr, que converte códigos numéricos em caracteres. As letras do alfabeto são codificadas em ordem alfabética, então, por exemplo:
>>> ord('c') - ord('a')
2
Porque 'c' é a “segunda” letra do alfabeto. Mas tenha cuidado: os códigos numéricos de letras maiúsculas são diferentes.
Piadas potencialmente ofensivas na internet às vezes são codificadas em ROT13, que é uma cifra de César com rotação 13. Se não se ofender facilmente, encontre e decifre algumas delas.
Capítulo 9: Estudo de caso: jogos de palavras
Este capítulo apresenta o segundo estudo de caso que envolve solucionar quebra-cabeças usando palavras com certas propriedades. Por exemplo, encontraremos os palíndromos mais longos em inglês e procuraremos palavras cujas letras apareçam em ordem alfabética. E apresentarei outro plano de desenvolvimento de programa: a redução a um problema resolvido anteriormente.
9.1 - Leitura de listas de palavras
Para os exercícios deste capítulo vamos usar uma lista de palavras em inglês. Há muitas listas de palavras disponíveis na internet, mas a mais conveniente ao nosso propósito é uma das listas de palavras disponibilizadas em domínio público por Grady Ward como parte do projeto lexical Moby (ver http://wikipedia.org/wiki/Moby_Project). É uma lista de 113.809 palavras cruzadas oficiais; isto é, as palavras que se consideram válidas em quebra-cabeças de palavras cruzadas e outros jogos de palavras. Na coleção Moby, o nome do arquivo é 113809of.fic; você pode baixar uma cópia, com um nome mais simples como words.txt, de http://thinkpython2.com/code/words.txt.
Este arquivo está em texto simples, então você pode abri-lo com um editor de texto, mas também pode lê-lo no Python. A função integrada open recebe o nome do arquivo como um parâmetro e retorna um objeto de arquivo que você pode usar para ler o arquivo.
>>> fin = open('words.txt')
fin é um nome comum de objeto de arquivo usado para entrada de dados. O objeto de arquivo oferece vários métodos de leitura, inclusive readline, que lê caracteres no arquivo até chegar a um comando de nova linha, devolvendo o resultado como uma string:
>>> fin.readline()
'aa\r\n'
A primeira palavra nesta lista específica é “aa”, uma espécie de lava. A sequência '\r\n' representa dois caracteres que representam espaços em branco (whitespace), um retorno de carro e uma nova linha, que separa esta palavra da seguinte.
O objeto de arquivo grava a posição em que está no arquivo, então se você chamar readline mais uma vez, receberá a seguinte palavra:
>>> fin.readline()
'aah\r\n'
A palavra seguinte é “aah”, uma palavra perfeitamente legítima, então pare de olhar para mim desse jeito. Ou, se é o whitespace que está incomodando você, podemos nos livrar dele com o método de string strip:
>>> line = fin.readline()
>>> word = line.strip()
>>> word
'aahed'
Você também pode usar um objeto de arquivo como parte de um loop for. Este programa lê words.txt e imprime cada palavra, uma por linha:
fin = open('words.txt')
for line in fin:
word = line.strip()
print(word)
9.2 - Exercícios
Há soluções para estes exercícios na próxima seção. Mas é bom você tentar fazer cada um antes de ver as soluções.
Exercício 9.1
Escreva um programa que leia words.txt e imprima apenas as palavras com mais de 20 caracteres (sem contar whitespace).
Exercício 9.2
Em 1939, Ernest Vincent Wright publicou uma novela de 50.000 palavras, chamada Gadsby, que não contém a letra “e”. Como o “e” é a letra mais comum em inglês, isso não é algo fácil de fazer.
Na verdade, é difícil até construir um único pensamento sem usar o símbolo mais comum do idioma. No início é lento, mas com prudência e horas de treino, vai ficando cada vez mais fácil.
Muito bem, agora eu vou parar.
Escreva uma função chamada has_no_e que retorne True se a palavra dada não tiver a letra “e” nela.
Altere seu programa na seção anterior para imprimir apenas as palavras que não têm “e” e calcule a porcentagem de palavras na lista que não têm “e”.
Exercício 9.3
Escreva uma função chamada avoids que receba uma palavra e uma série de letras proibidas, e retorne True se a palavra não usar nenhuma das letras proibidas.
Altere o código para que o usuário digite uma série de letras proibidas e o programa imprima o número de palavras que não contêm nenhuma delas. Você pode encontrar uma combinação de cinco letras proibidas que exclua o menor número possível de palavras?
Exercício 9.4
Escreva uma função chamada uses_only que receba uma palavra e uma série de letras e retorne True, se a palavra só contiver letras da lista. Você pode fazer uma frase usando só as letras acefhlo? Que não seja “Hoe alfalfa?”
Exercício 9.5
Escreva uma função chamada uses_all que receba uma palavra e uma série de letras obrigatórias e retorne True se a palavra usar todas as letras obrigatórias pelo menos uma vez. Quantas palavras usam todas as vogais (aeiou)? E que tal aeiouy?
Exercício 9.6
Escreva uma função chamada is_abecedarian que retorne True se as letras numa palavra aparecerem em ordem alfabética (tudo bem se houver letras duplas). Quantas palavras em ordem alfabética existem?
9.3 - Busca
Todos os exercícios na seção anterior têm algo em comum; eles podem ser resolvidos com o modelo de busca que vimos em Buscando. O exemplo mais simples é:
def has_no_e(word):
for letter in word:
if letter == 'e':
return False
return True
O loop for atravessa os caracteres em word. Se encontrarmos a letra “e”, podemos retornar False imediatamente; se não for o caso, temos que ir à letra seguinte. Se sairmos do loop normalmente, isso quer dizer que não encontramos um “e”, então retornamos True.
Você pode escrever esta função de forma mais concisa usando o operador in, mas comecei com esta versão porque ela demonstra a lógica do modelo de busca.
avoids é uma versão mais geral de has_no_e, mas tem a mesma estrutura:
def avoids(word, forbidden):
for letter in word:
if letter in forbidden:
return False
return True
Podemos retornar False logo que encontrarmos uma letra proibida; se chegarmos ao fim do loop, retornamos True.
uses_only é semelhante, exceto pelo sentido da condição, que se inverte:
def uses_only(word, available):
for letter in word:
if letter not in available:
return False
return True
Em vez de uma lista de letras proibidas, temos uma lista de letras disponíveis. Se encontrarmos uma letra em word que não está em available, podemos retornar False.
uses_all é semelhante, mas invertemos a função da palavra e a string de letras:
def uses_all(word, required):
for letter in required:
if letter not in word:
return False
return True
Em vez de atravessar as letras em word, o loop atravessa as letras obrigatórias. Se alguma das letras obrigatórias não aparecer na palavra, podemos retornar False.
Se você realmente estivesse pensando como um cientista da computação, teria reconhecido que uses_all foi um exemplo de um problema resolvido anteriormente e escreveria:
def uses_all(word, required):
return uses_only(required, word)
Esse é um exemplo de um plano de desenvolvimento de programa chamado redução a um problema resolvido anteriormente, ou seja, você reconhece o problema no qual está trabalhando como um exemplo de um problema já resolvido e aplica uma solução existente.
9.4 - Loop com índices
Escrevi as funções na seção anterior com loops for porque eu só precisava dos caracteres nas strings; não precisava fazer nada com os índices.
Para is_abecedarian temos que comparar letras adjacentes, o que é um pouco complicado para o loop for:
def is_abecedarian(word):
previous = word[0]
for c in word:
if c < previous:
return False
previous = c
return True
Uma alternativa é usar a recursividade:
def is_abecedarian(word):
if len(word) <= 1:
return True
if word[0] > word[1]:
return False
return is_abecedarian(word[1:])
Outra opção é usar um loop while:
def is_abecedarian(word):
i = 0
while i < len(word)-1:
if word[i+1] < word[i]:
return False
i = i+1
return True
O loop começa com i == 0 e termina quando i == len(word)-1. Cada vez que passa pelo loop, o programa compara o “i-ésimo” caractere (que você pode considerar o caractere atual) com o caractere de posição i+1 (que pode ser considerado o caractere seguinte).
Se o próximo caractere for de uma posição anterior (alfabeticamente anterior) à atual, então descobrimos uma quebra na tendência alfabética, e retornamos False.
Se chegarmos ao fim do loop sem encontrar uma quebra, então a palavra passa no teste. Para convencer-se de que o loop termina corretamente, considere um exemplo como 'flossy'. O comprimento da palavra é 6, então o loop é executado pela última vez quando i for igual a 4, que é o índice do segundo caractere de trás para frente. Na última iteração, o programa compara o penúltimo caractere com o último, que é o que queremos.
Aqui está uma versão de is_palindrome (veja o Exercício 6.3) que usa dois índices: um começa no início e aumenta; o outro começa no final e diminui.
def is_palindrome(word):
i = 0
j = len(word)-1
while i<j:
if word[i] != word[j]:
return False
i = i+1
j = j-1
return True
Ou podemos reduzir a um problema resolvido anteriormente e escrever:
def is_palindrome(word):
return is_reverse(word, word)
Usando is_reverse da seção 8.11.
9.5 - Depuração
Testar programas é difícil. As funções neste capítulo são relativamente fáceis para testar porque é possível verificar os resultados à mão. Ainda assim, pode ser difícil ou até impossível escolher um grupo de palavras que teste todos os erros possíveis.
Tomando has_no_e como exemplo, há dois casos óbvios para verificar: as palavras que têm um ‘e’ devem retornar False, e as palavras que não têm devem retornar True. Não deverá ser um problema pensar em um exemplo de cada uma.
Dentro de cada caso, há alguns subcasos menos óbvios. Entre as palavras que têm um “e”, você deve testar palavras com um “e” no começo, no fim e em algum lugar no meio. Você deve testar palavras longas, palavras curtas e palavras muito curtas, como a string vazia. A string vazia é um exemplo de um caso especial, não óbvio, onde erros muitas vezes espreitam.
Além dos casos de teste que você gerar, também pode ser uma boa ideia testar seu programa com uma lista de palavras como words.txt. Ao analisar a saída, pode ser que os erros apareçam, mas tenha cuidado: você pode pegar um tipo de erro (palavras que não deveriam ser incluídas, mas foram) e não outro (palavras que deveriam ser incluídas, mas não foram).
Em geral, o teste pode ajudar a encontrar bugs, mas não é fácil gerar um bom conjunto de casos de teste, e, mesmo se conseguir, não há como ter certeza de que o programa está correto. Segundo um lendário cientista da computação:
Testar programas pode ser usado para mostrar a presença de bugs, mas nunca para mostrar a ausência deles! – Edsger W. Dijkstra
9.6 - Glossário
objeto de arquivo
Um valor que representa um arquivo aberto.
redução a um problema resolvido anteriormente
Um modo de resolver um problema expressando-o como uma instância de um problema resolvido anteriormente.
caso especial
Um caso de teste que é atípico ou não é óbvio (e com probabilidade menor de ser tratado corretamente).
9.7 - Exercícios
Exercício 9.7
Esta pergunta é baseada em um quebra-cabeça veiculado em um programa de rádio chamado Car Talk (http://www.cartalk.com/content/puzzlers):
Dê uma palavra com três letras duplas consecutivas. Vou dar exemplos de palavras que quase cumprem a condição, mas não chegam lá. Por exemplo, a palavra committee, c-o-m-m-i-t-t-e-e. Seria perfeita se não fosse aquele ‘i’ que se meteu ali no meio. Ou Mississippi: M-i-s-s-i-s-s-i-p-p-i. Se pudesse tirar aqueles ‘is’, daria certo. Mas há uma palavra que tem três pares consecutivos de letras e, que eu saiba, pode ser a única palavra que existe. É claro que provavelmente haja mais umas 500, mas só consigo pensar nessa. Qual é a palavra?
Escreva um programa que a encontre.
Solução: http://thinkpython2.com/code/cartalk1.py.
Exercício 9.8
Aqui está outro quebra-cabeça do programa Car Talk (http://www.cartalk.com/content/puzzlers):
“Estava dirigindo outro dia e percebi algo no hodômetro que chamou a minha atenção. Como a maior parte dos hodômetros, ele mostra seis dígitos, apenas em milhas inteiras. Por exemplo, se o meu carro tivesse 300.000 milhas, eu veria 3-0-0-0-0-0.
“Agora, o que vi naquele dia foi muito interessante. Notei que os últimos 4 dígitos eram um palíndromo; isto é, podiam ser lidos da mesma forma no sentido correto e no sentido inverso. Por exemplo, 5-4-4-5 é um palíndromo, então no meu hodômetro poderia ser 3-1-5-4-4-5.
“Uma milha depois, os últimos 5 números formaram um palíndromo. Por exemplo, poderia ser 3-6-5-4-5-6. Uma milha depois disso, os 4 números do meio, dentro dos 6, formavam um palíndromo. E adivinhe só? Um milha depois, todos os 6 formavam um palíndromo!
“A pergunta é: o que estava no hodômetro quando olhei primeiro?”
Escreva um programa Python que teste todos os números de seis dígitos e imprima qualquer número que satisfaça essas condições.
Solução: http://thinkpython2.com/code/cartalk2.py.
Exercício 9.9
Aqui está outro problema do Car Talk que você pode resolver com uma busca (http://www.cartalk.com/content/puzzlers):
“Há pouco tempo recebi uma visita da minha mãe e percebemos que os dois dígitos que compõem a minha idade, quando invertidos, representavam a idade dela. Por exemplo, se ela tem 73 anos, eu tenho 37 anos. Ficamos imaginando com que frequência isto aconteceu nos anos anteriores, mas acabamos mudando de assunto e não chegamos a uma resposta.
“Quando cheguei em casa, cheguei à conclusão de que os dígitos das nossas idades tinham sido reversíveis seis vezes até então. Também percebi que, se tivéssemos sorte, isso aconteceria novamente dali a alguns anos, e se fôssemos muito sortudos, aconteceria mais uma vez depois disso. Em outras palavras, aconteceria 8 vezes no total. Então a pergunta é: quantos anos tenho agora?”
Escreva um programa em Python que busque soluções para esse problema. Dica: pode ser uma boa ideia usar o método de string zfill.
Capítulo 10: Listas
Este capítulo apresenta um dos tipos integrados mais úteis do Python: listas. Você também aprenderá mais sobre objetos e o que pode acontecer quando o mesmo objeto tem mais de um nome.
10.1 - Uma lista é uma sequência
Como uma string, uma lista é uma sequência de valores. Em uma string, os valores são caracteres; em uma lista, eles podem ser de qualquer tipo. Os valores em uma lista são chamados de elementos, ou, algumas vezes, de itens.
Há várias formas para criar uma lista; a mais simples é colocar os elementos entre colchetes ([ e ]):
[10, 20, 30, 40]
['crunchy frog', 'ram bladder', 'lark vomit']
O primeiro exemplo é uma lista de quatro números inteiros. O segundo é uma lista de três strings. Os elementos de uma lista não precisam ser do mesmo tipo. A lista seguinte contém uma string, um número de ponto flutuante, um número inteiro e (olhe só!) outra lista:
['spam', 2.0, 5, [10, 20]]
Uma lista dentro de outra lista é uma lista aninhada.
Uma lista que não contém elementos é chamada de lista vazia; você pode criar uma com colchetes vazios [].
Como já se poderia esperar, podemos atribuir uma lista de valores a variáveis:
>>> cheeses = ['Cheddar', 'Edam', 'Gouda']
>>> numbers = [42, 123]
>>> empty = []
>>> print(cheeses, numbers, empty)
['Cheddar', 'Edam', 'Gouda'] [42, 123] []
10.2 - Listas são mutáveis
A sintaxe para acessar os elementos de uma lista é a mesma que para acessar os caracteres de uma string: o operador de colchete. A expressão dentro dos colchetes especifica o índice. Lembre-se de que os índices começam em 0:
>>> cheeses[0]
'Cheddar'
Diferente das strings, listas são mutáveis. Quando o operador de colchete aparece do lado esquerdo de uma atribuição, ele identifica o elemento da lista que será atribuído:
>>> numbers = [42, 123]
>>> numbers[1] = 5
>>> numbers
[42, 5]
O primeiro elemento de numbers, que costumava ser 123, agora é 5.
A Figura 10.1 mostra o diagrama de estado para cheeses, numbers e empty.
 .
.
Figura 10.1 – Diagrama de estado de três listas.
As listas são representadas pelas caixas com a palavra “lista” fora delas e os elementos da lista dentro delas. cheeses refere-se a uma lista com três elementos indexados como 0, 1 e 2. numbers contém dois elementos e o diagrama mostra que o valor do segundo elemento foi reatribuído de 123 para 5. empty refere-se a uma lista sem elementos.
Índices de listas funcionam da mesma forma que os índices de strings:
-
Qualquer expressão de números inteiros pode ser usada como índice.
-
Se tentar ler ou escrever um elemento que não existe, você recebe um IndexError.
-
Se um índice tiver um valor negativo, ele conta de trás para a frente, a partir do final da lista.
O operador in também funciona com listas:
>>> cheeses = ['Cheddar', 'Edam', 'Gouda']
>>> 'Edam' in cheeses
True
>>> 'Brie' in cheeses
False
10.3 - Percorrendo uma lista
A forma mais comum de percorrer os elementos em uma lista é com um loop for. A sintaxe é a mesma que a das strings:
for cheese in cheeses:
print(cheese)
Isso funciona bem se você precisa apenas ler os elementos da lista. Mas se você quer escrever ou atualizar os elementos, você precisa dos índices. Uma forma comum de fazer isso é combinar as funções integradas range e len:
for i in range(len(numbers)):
numbers[i] = numbers[i] * 2
Este loop percorre a lista e atualiza cada elemento. len retorna o número de elementos na lista. range retorna uma lista de índices de 0 a n-1, em que n é o comprimento da lista. Cada vez que passa pelo loop, i recebe o índice do próximo elemento. A instrução de atribuição no corpo usa i para ler o valor antigo do elemento e atribuir o novo valor.
Um loop for que passe por uma lista vazia nunca executa o corpo:
for x in []:
print('This never happens.')
Apesar de uma lista poder conter outra lista, a lista aninhada ainda conta como um único elemento. O comprimento desta lista é quatro:
['spam', 1, ['Brie', 'Roquefort', 'Pol le Veq'], [1, 2, 3]]
10.4 - Operações com listas
O operador + concatena listas:
>>> a = [1, 2, 3]
>>> b = [4, 5, 6]
>>> c = a + b
>>> c
[1, 2, 3, 4, 5, 6]
O operador * repete a lista um dado número de vezes:
>>> [0] * 4
[0, 0, 0, 0]
>>> [1, 2, 3] * 3
[1, 2, 3, 1, 2, 3, 1, 2, 3]
O primeiro exemplo repete [0] quatro vezes. O segundo exemplo repete a lista [1, 2, 3] três vezes.
10.5 - Fatias de listas
O operador de fatiamento também funciona com listas:
>>> t = ['a', 'b', 'c', 'd', 'e', 'f']
>>> t[1:3]
['b', 'c']
>>> t[:4]
['a', 'b', 'c', 'd']
>>> t[3:]
['d', 'e', 'f']
Se você omitir o primeiro índice, a fatia começa no início. Se você omitir o segundo, a fatia vai até o final. Se você omitir ambos, a fatia é uma cópia da lista inteira.
>>> t[:]
['a', 'b', 'c', 'd', 'e', 'f']
Como as listas são mutáveis, pode ser útil fazer uma cópia antes de executar operações que as alterem.
Um operador de fatia à esquerda de uma atribuição pode atualizar vários elementos:
>>> t = ['a', 'b', 'c', 'd', 'e', 'f']
>>> t[1:3] = ['x', 'y']
>>> t
['a', 'x', 'y', 'd', 'e', 'f']
10.6 - Métodos de listas
O Python oferece métodos que operam em listas. Por exemplo, append adiciona um novo elemento ao fim de uma lista:
>>> t = ['a', 'b', 'c']
>>> t.append('d')
>>> t
['a', 'b', 'c', 'd']
extend toma uma lista como argumento e adiciona todos os elementos:
>>> t1 = ['a', 'b', 'c']
>>> t2 = ['d', 'e']
>>> t1.extend(t2)
>>> t1
['a', 'b', 'c', 'd', 'e']
Este exemplo deixa t2 intocado.
sort classifica os elementos da lista em ordem ascendente:
>>> t = ['d', 'c', 'e', 'b', 'a']
>>> t.sort()
>>> t
['a', 'b', 'c', 'd', 'e']
A maior parte dos métodos de listas são nulos; eles alteram a lista e retornam None. Se você escrever t = t.sort() por acidente, ficará desapontado com o resultado.
10.7 - Mapeamento, filtragem e redução
Para somar o total de todos os números em uma lista, você pode usar um loop como esse:
def add_all(t):
total = 0
for x in t:
total += x
return total
total é inicializado com 0. Cada vez que o programa passa pelo loop, x recebe um elemento da lista. O operador += oferece uma forma curta de atualizar uma variável. Esta instrução de atribuição aumentada,
total += x
é equivalente a
total = total + x
No decorrer da execução do loop, total acumula a soma dos elementos; uma variável usada desta forma às vezes é chamada de acumuladora.
Somar todos elementos de uma lista é uma operação tão comum que o Python a oferece como uma função integrada, sum:
>>> t = [1, 2, 3]
>>> sum(t)
6
Uma operação como essa, que combina uma sequência de elementos em um único valor, às vezes é chamada de redução.
Algumas vezes você quer percorrer uma lista enquanto cria outra. Por exemplo, a função seguinte recebe uma lista de strings e retorna uma nova lista que contém strings com letras maiúsculas:
def capitalize_all(t):
res = []
for s in t:
res.append(s.capitalize())
return res
res é inicializado com uma lista vazia; cada vez que o programa passa pelo loop, acrescentamos o próximo elemento. Então res é outro tipo de acumulador.
Uma operação como capitalize_all às vezes é chamada de mapeamento porque ela “mapeia” uma função (nesse caso o método capitalize) sobre cada um dos elementos em uma sequência.
Outra operação comum é selecionar alguns dos elementos de uma lista e retornar uma sublista. Por exemplo, a função seguinte recebe uma lista de strings e retorna uma lista que contém apenas strings em letra maiúscula:
def only_upper(t):
res = []
for s in t:
if s.isupper():
res.append(s)
return res
isupper é um método de string que retorna True se a string contiver apenas letras maiúsculas.
Uma operação como only_upper é chamada de filtragem porque filtra alguns dos elementos e desconsidera outros.
As operações de lista mais comuns podem ser expressas como uma combinação de mapeamento, filtragem e redução.
10.8 - Como excluir elementos
Há várias formas de excluir elementos de uma lista. Se souber o índice do elemento que procura, você pode usar pop:
>>> t = ['a', 'b', 'c']
>>> x = t.pop(1)
>>> t
['a', 'c']
>>> x
'b'
pop altera a lista e retorna o elemento que foi excluído. Se você não incluir um índice, ele exclui e retorna o último elemento.
Se não precisar do valor removido, você pode usar a instrução del:
>>> t = ['a', 'b', 'c']
>>> del t[1]
>>> t
['a', 'c']
Se souber o elemento que quer excluir (mas não o índice), você pode usar remove:
>>> t = ['a', 'b', 'c']
>>> t.remove('b')
>>> t
['a', 'c']
O valor devolvido por remove é None.
Para remover mais de um elemento, você pode usar del com um índice de fatia:
>>> t = ['a', 'b', 'c', 'd', 'e', 'f']
>>> del t[1:5]
>>> t
['a', 'f']
Como sempre, a fatia seleciona todos os elementos até, mas não incluindo, o segundo índice.
10.9 - Listas e strings
Uma string é uma sequência de caracteres e uma lista é uma sequência de valores, mas uma lista de caracteres não é a mesma coisa que uma string. Para converter uma string em uma lista de caracteres, você pode usar list:
>>> s = 'spam'
>>> t = list(s)
>>> t
['s', 'p', 'a', 'm']
Como list é o nome de uma função integrada, você deve evitar usá-lo como nome de variável. Também evito usar l porque parece demais com 1. É por isso que uso t.
A função list quebra uma string em letras individuais. Se você quiser quebrar uma string em palavras, você pode usar o método split:
>>> s = 'pining for the fjords'
>>> t = s.split()
>>> t
['pining', 'for', 'the', 'fjords']
Um argumento opcional chamado delimiter especifica quais caracteres podem ser usados para demonstrar os limites das palavras. O exemplo seguinte usa um hífen como delimitador:
>>> s = 'spam-spam-spam'
>>> delimiter = '-'
>>> t = s.split(delimiter)
>>> t
['spam', 'spam', 'spam']
join é o contrário de split. Ele toma uma lista de strings e concatena os elementos. join é um método de string, então é preciso invocá-lo no delimitador e passar a lista como parâmetro:
>>> t = ['pining', 'for', 'the', 'fjords']
>>> delimiter = ' '
>>> s = delimiter.join(t)
>>> s
'pining for the fjords'
Nesse caso, o delimitador é um caractere de espaço, então join coloca um espaço entre as palavras. Para concatenar strings sem espaços, você pode usar a string vazia '', como delimitador.
10.10 - Objetos e valores
Se executarmos essas instruções de atribuição:
a = 'banana'
b = 'banana'
Sabemos que a e b se referem a uma string, mas não sabemos se elas se referem à mesma string. Há dois estados possíveis, mostrados na Figura 10.2.
 .
.
Figura 10.2 – Diagramas de estado possíveis com duas variáveis.
Em um caso, a e b se referem a dois objetos diferentes que têm o mesmo valor. No segundo caso, elas se referem ao mesmo objeto.
Para verificar se duas variáveis se referem ao mesmo objeto, você pode usar o operador is:
>>> a = 'banana'
>>> b = 'banana'
>>> a is b
True
Nesse exemplo, o Python criou apenas um objeto de string e tanto a quanto b se referem a ele. Mas quando você cria duas listas, você tem dois objetos:
>>> a = [1, 2, 3]
>>> b = [1, 2, 3]
>>> a is b
False
Então o diagrama de estado fica igual ao da Figura 10.3.
 .
.
Figura 10.3 – Diagrama de estado com variáveis associadas a listas distintas, de mesmo valor.
Nesse caso, diríamos que as duas listas são equivalentes, porque elas têm os mesmos elementos, mas não idênticas, porque elas não são o mesmo objeto. Se dois objetos forem idênticos, eles também são equivalentes, mas se eles forem equivalentes, não são necessariamente idênticos.
Até agora, temos usado “objeto” e “valor” de forma intercambiável, mas é mais exato dizer que um objeto tem um valor. Se avaliar [1, 2, 3], você tem um objeto de lista cujo valor é uma sequência de números inteiros. Se outra lista tem os mesmos elementos, dizemos que tem o mesmo valor, mas não é o mesmo objeto.
10.11 - Alias
Se a se refere a um objeto e você atribui b = a, então ambas as variáveis se referem ao mesmo objeto.
>>> a = [1, 2, 3]
>>> b = a
>>> b is a
True
O diagrama de estado ficará igual à Figura 10.4.
 .
.
Figura 10.4 – Diagrama de estado com duas variáveis associadas à mesma lista.
A associação de uma variável com um objeto é chamada de referência. Neste exemplo, há duas referências ao mesmo objeto.
Um objeto com mais de uma referência tem mais de um nome, então dizemos que o objeto tem um alias.
Se o objeto com alias é mutável, alterações feitas em um alias afetam o outro também.
>>> b[0] = 42
>>> a
[42, 2, 3]
Apesar de esse comportamento poder ser útil, ele é passível de erros. Em geral, é mais seguro evitar usar alias ao trabalhar com objetos mutáveis.
Para objetos imutáveis como strings, usar alias não é um problema tão grande. Neste exemplo:
a = 'banana'
b = 'banana'
Quase nunca faz diferença se a e b se referem à mesma string ou não.
10.12 - Argumentos de listas
Ao passar uma lista a uma função, a função recebe uma referência à lista. Se a função alterar a lista, quem faz a chamada vê a mudança. Por exemplo, delete_head remove o primeiro elemento de uma lista:
def delete_head(t):
del t[0]
Ela é usada assim:
>>> letters = ['a', 'b', 'c']
>>> delete_head(letters)
>>> letters
['b', 'c']
O parâmetro t e a variável letters são alias para o mesmo objeto. O diagrama da pilha fica igual ao da Figura 10.5.
 .
.
Figura 10.5 – Diagrama da pilha: __main__ e delete_head compartilham referências à mesma lista.
Como a lista é compartilhada por dois frames, desenhei-a entre eles.
É importante distinguir entre operações que alteram listas e operações que criam novas listas. Por exemplo, o método append altera a lista, mas o operador + cria uma nova lista:
>>> t1 = [1, 2]
>>> t2 = t1.append(3)
>>> t1
[1, 2, 3]
>>> t2
None
Note que append altera a lista e retorna None (na realidade, o console do Python omite o None da saída, mas você pode conferir usando t2 is None).
>>> t3 = t1 + [4]
>>> t1
[1, 2, 3]
>>> t3
[1, 2, 3, 4]
>>> t1
O operador + cria uma nova lista e deixa a lista original inalterada.
Essa diferença é importante quando você escreve funções que devem alterar listas. Por exemplo, esta função não remove a cabeça de uma lista:
def bad_delete_head(t):
t = t[1:] # ERRADO!
O operador de fatia cria uma nova lista e a atribuição faz t se referir a ela, mas isso não afeta quem faz chamada.
>>> t4 = [1, 2, 3]
>>> bad_delete_head(t4)
>>> t4
[1, 2, 3]
No início de bad_delete_head, t e t4 se referem à mesma lista. No final, t se refere a uma nova lista, mas t4 ainda se refere à lista original, inalterada.
Uma alternativa é escrever uma função que crie e retorne uma nova lista. Por exemplo, tail retorna tudo, exceto o primeiro elemento de uma lista:
def tail(t):
return t[1:]
Esta função deixa a lista original inalterada. Ela é usada assim:
>>> letters = ['a', 'b', 'c']
>>> rest = tail(letters)
>>> rest
['b', 'c']
10.13 - Depuração
O uso descuidado de listas (e de outros objetos mutáveis) pode levar a longas horas de depuração. Aqui estão algumas armadilhas comuns e formas de evitá-las:
- A maior parte dos métodos de listas alteram o argumento e retornam None. Isto é o oposto dos métodos de strings, que retornam uma nova string e deixam a original intocada.
Se você está acostumado a escrever código de strings desta forma:
word = word.strip()
É tentador escrever código de listas como este:
t = t.sort() # ERRADO!
Como sort retorna None, a próxima operação que você executar com t provavelmente vai falhar.
Antes de usar métodos e operadores de listas, você deve ler a documentação com cuidado e testá-los no modo interativo.
- Escolha o termo e fique com ele.
Parte do problema com listas é que há muitas formas de fazer coisas com elas. Por exemplo, para remover um elemento de uma lista você pode usar pop, remove, del ou até uma atribuição de fatia.
Para adicionar um elemento você pode usar o método append ou o operador +. Assumindo que t é uma lista e x é um elemento da lista, isto está correto:
t.append(x)
t = t + [x]
t += [x]
E isto está errado:
t.append([x]) # ERRADO!
t = t.append(x) # ERRADO!
t + [x] # ERRADO!
t = t + x # ERRADO!
Experimente cada um desses exemplos no modo interativo para conferir se você entendeu o que fazem. Note que apenas o último causa um erro de tempo de execução; os outros três são legais, mas eles fazem a coisa errada.
- Faça cópias para evitar o uso de alias.
Se quiser usar um método como sort, que altera o argumento, mas precisa manter a lista original, você pode fazer uma cópia:
>>> t = [3, 1, 2]
>>> t2 = t[:]
>>> t2.sort()
>>> t
[3, 1, 2]
>>> t2
[1, 2, 3]
Neste exemplo você poderia usar também a função integrada sorted, que retorna uma nova lista classificada e deixa a original intocada.
>>> t2 = sorted(t)
>>> t
[3, 1, 2]
>>> t2
[1, 2, 3]
10.14 - Glossário
lista
Uma sequência de valores.
elemento
Um dos valores em uma lista (ou outra sequência), também chamado de item.
lista aninhada
Uma lista que é um elemento de outra lista.
acumuladora
Variável usada em um loop para adicionar ou acumular um resultado.
atribuição aumentada
Instrução que atualiza o valor de uma variável usando um operador como +=.
redução
Padrão de processamento que atravessa uma sequência e acumula os elementos em um único resultado.
mapeamento
Padrão de processamento que atravessa uma sequência e executa uma operação em cada elemento.
filtragem
Padrão de processamento que atravessa uma lista e seleciona os elementos que satisfazem algum critério.
objeto
Algo a que uma variável pode se referir. Um objeto tem um tipo e um valor.
equivalente
Ter o mesmo valor.
idêntico
Ser o mesmo objeto (o que implica equivalência).
referência
Associação entre uma variável e seu valor.
alias
Uma circunstância onde duas ou mais variáveis se referem ao mesmo objeto.
delimitador
Um caractere ou uma string usada para indicar onde uma string deve ser dividida.
10.15 - Exercícios
Você pode baixar as soluções para estes exercícios em http://thinkpython2.com/code/list_exercises.py.
Exercício 10.1
Escreva uma função chamada nested_sum que receba uma lista de listas de números inteiros e adicione os elementos de todas as listas aninhadas. Por exemplo:
>>> t = [[1, 2], [3], [4, 5, 6]]
>>> nested_sum(t)
21
Exercício 10.2
Escreva uma função chamada cumsum que receba uma lista de números e retorne a soma cumulativa; isto é, uma nova lista onde o i-ésimo elemento é a soma dos primeiros i+1 elementos da lista original. Por exemplo:
>>> t = [1, 2, 3]
>>> cumsum(t)
[1, 3, 6]
Exercício 10.3
Escreva uma função chamada middle que receba uma lista e retorne uma nova lista com todos os elementos originais, exceto os primeiros e os últimos elementos. Por exemplo:
>>> t = [1, 2, 3, 4]
>>> middle(t)
[2, 3]
Exercício 10.4
Escreva uma função chamada chop que tome uma lista alterando-a para remover o primeiro e o último elementos, e retorne None. Por exemplo:
>>> t = [1, 2, 3, 4]
>>> chop(t)
>>> t
[2, 3]
Exercício 10.5
Escreva uma função chamada is_sorted que tome uma lista como parâmetro e retorne True se a lista estiver classificada em ordem ascendente, e False se não for o caso. Por exemplo:
>>> is_sorted([1, 2, 2])
True
>>> is_sorted(['b', 'a'])
False
Exercício 10.6
Duas palavras são anagramas se você puder soletrar uma rearranjando as letras da outra. Escreva uma função chamada is_anagram que tome duas strings e retorne True se forem anagramas.
Exercício 10.7
Escreva uma função chamada has_duplicates que tome uma lista e retorne True se houver algum elemento que apareça mais de uma vez. Ela não deve modificar a lista original.
Exercício 10.8
Este exercício pertence ao assim chamado Paradoxo de aniversário, sobre o qual você pode ler em http://en.wikipedia.org/wiki/Birthday_paradox.
Se há 23 alunos na sua sala, quais são as chances de dois deles fazerem aniversário no mesmo dia? Você pode estimar esta probabilidade gerando amostras aleatórias de 23 dias de aniversário e verificando as correspondências. Dica: você pode gerar aniversários aleatórios com a função randint no módulo random.
Se quiser, você pode baixar minha solução em http://thinkpython2.com/code/birthday.py.
Exercício 10.9
Escreva uma função que leia o arquivo words.txt e construa uma lista com um elemento por palavra. Escreva duas versões desta função, uma usando o método append e outra usando a expressão t = t + [x]. Qual leva mais tempo para ser executada? Por quê?
Solução: http://thinkpython2.com/code/wordlist.py.
Exercício 10.10
Para verificar se uma palavra está na lista de palavras, você pode usar o operador in, mas isso seria lento porque pesquisaria as palavras em ordem.
Como as palavras estão em ordem alfabética, podemos acelerar as coisas com uma busca por bisseção (também conhecida como pesquisa binária), que é semelhante ao que você faz quando procura uma palavra no dicionário. Você começa no meio e verifica se a palavra que está procurando vem antes da palavra no meio da lista. Se for o caso, procura na primeira metade da lista. Se não, procura na segunda metade.
De qualquer forma, você corta o espaço de busca restante pela metade. Se a lista de palavras tiver 113.809 palavras, o programa seguirá uns 17 passos para encontrar a palavra ou concluir que não está lá.
Escreva uma função chamada in_bisect que receba uma lista ordenada, um valor-alvo e devolva o índice do valor na lista se ele estiver lá, ou None se não estiver.
Ou você pode ler a documentação do módulo bisect e usá-lo!
Solução: http://thinkpython2.com/code/inlist.py.
Exercício 10.11
Duas palavras são um “par inverso” se uma for o contrário da outra. Escreva um programa que encontre todos os pares inversos na lista de palavras.
Solução: http://thinkpython2.com/code/reverse_pair.py.
Exercício 10.12
Duas palavras “interligam-se” quando, ao tomarmos letras alternadas de cada uma, formamos uma palavra nova. Por exemplo, “shoe” e “cold” interligam-se para formar “schooled”.
Solução: http://thinkpython2.com/code/interlock.py. Crédito: este exercício foi inspirado por um exemplo em http://puzzlers.org.
-
Escreva um programa que encontre todos os pares de palavras que se interligam. Dica: não enumere todos os pares!
-
Você pode encontrar palavras que sejam interligadas de três em três; isto é, cada terceira letra forma uma palavra, começando da primeira, segunda ou terceira?
Capítulo 11: Dicionários
Este capítulo apresenta outro tipo integrado chamado dicionário. Dicionários são um dos melhores recursos do Python; eles são os blocos de montar de muitos algoritmos eficientes e elegantes.
11.1 - Um dicionário é um mapeamento
Um dicionário se parece com uma lista, mas é mais geral. Em uma lista, os índices têm que ser números inteiros; em um dicionário, eles podem ser de (quase) qualquer tipo.
Um dicionário contém uma coleção de índices, que se chamam chaves e uma coleção de valores. Cada chave é associada com um único valor. A associação de uma chave e um valor chama-se par chave-valor ou item.
Em linguagem matemática, um dicionário representa um mapeamento de chaves a valores, para que você possa dizer que cada chave “mostra o mapa a” um valor. Como exemplo, vamos construir um dicionário que faz o mapa de palavras do inglês ao espanhol, portanto as chaves e os valores são todos strings.
A função dict cria um novo dicionário sem itens. Como dict é o nome de uma função integrada, você deve evitar usá-lo como nome de variável.
>>> eng2sp = dict()
>>> eng2sp
{}
As chaves {} representam um dicionário vazio. Para acrescentar itens ao dicionário, você pode usar colchetes:
>>> eng2sp['one'] = 'uno'
Esta linha cria um item que mapeia da chave 'one' ao valor 'uno'. Se imprimirmos o dicionário novamente, vemos um par chave-valor com dois pontos entre a chave e o valor:
>>> eng2sp
{'one': 'uno'}
Este formato de saída também é um formato de entrada. Por exemplo, você pode criar um dicionário com três itens:
>>> eng2sp = {'one': 'uno', 'two': 'dos', 'three': 'tres'}
Porém, se exibir eng2sp, pode se surpreender:
>>> eng2sp
{'one': 'uno', 'three': 'tres', 'two': 'dos'}
A ordem dos pares chave-valor pode não ser a mesma. Se você digitar o mesmo exemplo no seu computador, pode receber um resultado diferente. Em geral, a ordem dos itens em um dicionário é imprevisível.
No entanto, isso não é um problema porque os elementos de um dicionário nunca são indexados com índices de números inteiros. Em vez disso, você usa as chaves para procurar os valores correspondentes:
>>> eng2sp['two']
'dos'
A chave 'two' sempre mapeia ao valor 'dos', assim a ordem dos itens não importa.
Se a chave não estiver no dicionário, você recebe uma exceção:
>>> eng2sp['four']
KeyError: 'four'
A função len é compatível com dicionários; ela devolve o número de pares chave-valor:
>>> len(eng2sp)
3
O operador in funciona em dicionários também; ele acusa se algo aparece como chave no dicionário (aparecer como valor não é o suficiente).
>>> 'one' in eng2sp
True
>>> 'uno' in eng2sp
False
Para ver se algo aparece como um valor em um dicionário, você pode usar o método values, que devolve uma coleção de valores, e então usar o operador in:
>>> vals = eng2sp.values()
>>> 'uno' in vals
True
O operador in usa algoritmos diferentes para listas e dicionários. Para listas, ele procura os elementos da lista em ordem, como descrito em “Busca”, na página 123. Conforme a lista torna-se mais longa, o tempo de busca também fica proporcionalmente mais longo.
Para dicionários, o Python usa um algoritmo chamado hashtable (tabela de dispersão), que tem uma propriedade notável: o operador in leva praticamente o mesmo tempo na busca, não importa quantos itens estejam no dicionário. Eu explico como isso é possível em “Hashtables”, na página 302, mas a explicação pode não fazer sentido até que você tenha lido mais alguns capítulos.
11.2 - Um dicionário como uma coleção de contadores
Suponha que você receba uma string e queira contar quantas vezes cada letra aparece nela. Há vários modos de fazer isso:
-
Você pode criar 26 variáveis, uma para cada letra do alfabeto. Então pode atravessar a string e, para cada caractere, incrementar o contador correspondente, provavelmente usando uma condicional encadeada.
-
Você pode criar uma lista com 26 elementos. Então pode converter cada caractere em um número (com a função integrada ord), usar o número como índice na lista e incrementar o respectivo contador.
-
Você pode criar um dicionário com caracteres como chaves e contadores como valores correspondentes. Na primeira vez que visse um caractere, você acrescentaria um item ao dicionário. Depois disso, incrementaria o valor de um item existente.
Cada uma dessas opções executa o mesmo cálculo, mas o implementa de forma diferente.
Uma implementação é um modo de executar um cálculo; algumas implementações são melhores que outras. Por exemplo, uma vantagem da implementação de dicionários é que não precisamos saber de antemão quais letras aparecem na string e só é preciso criar espaço para as letras que realmente venham a aparecer.
O código poderia ser assim:
def histogram(s):
d = dict()
for c in s:
if c not in d:
d[c] = 1
else:
d[c] += 1
return d
O nome da função é histogram, um termo estatístico para uma coleção de contadores (ou frequências).
A primeira linha da função cria um dicionário vazio. O loop for atravessa a string. Cada vez que passa pelo loop, se o caractere c não estiver no dicionário, criamos um item com a chave c e o valor inicial 1 (pois já vimos esta letra uma vez). Se o c já estiver no dicionário, incrementamos d [c].
Funciona assim:
>>> h = histogram('brontosaurus')
>>> h
{'a': 1, 'b': 1, 'o': 2, 'n': 1, 's': 2, 'r': 2, 'u': 2, 't': 1}
O histograma indica que as letras 'a' e 'b' aparecem uma vez; 'o' aparece duas vezes, e assim por diante.
Os dicionários têm um método chamado get, que toma uma chave e um valor padrão. Se a chave aparecer no dicionário, get retorna o valor correspondente; se não for o caso, ele retorna o valor padrão. Por exemplo:
>>> h = histogram('a')
>>> h
{'a': 1}
>>> h.get('a', 0)
1
>>> h.get('b', 0)
0
Como exercício, use o get para escrever a função histogram de forma mais concisa. Tente eliminar a instrução if.
11.3 - Loop e dicionários
Se usar um dicionário em uma instrução for, ela percorre as chaves do dicionário. Por exemplo, print_hist exibe cada chave e o valor correspondente:
def print_hist(h):
for c in h:
print(c, h[c])
Isso é o que aparece:
>>> h = histogram('parrot')
>>> print_hist(h)
a 1
p 1
r 2
t 1
o 1
Novamente, as chaves não estão em nenhuma ordem determinada. Para atravessar as chaves em ordem ascendente, você pode usar a função integrada sorted:
>>> for key in sorted(h):
... print(key, h[key])
a 1
o 1
p 1
r 2
t 1
11.4 - Busca reversa
Considerando um dicionário d e uma chave k, é fácil encontrar o valor correspondente v = d [k]. Esta operação chama-se busca.
Mas e se você tiver v e quiser encontrar k? Você tem dois problemas: em primeiro lugar, pode haver mais de uma chave que esteja mapeada ao valor v. Dependendo da aplicação, quem sabe você pode escolher um, ou talvez tenha de fazer uma lista que contenha todos eles. Em segundo lugar, não há sintaxe simples para fazer uma busca reversa; é preciso procurar.
Aqui está uma função que recebe um valor e retorna a primeira chave mapeada ao valor dado:
def reverse_lookup(d, v):
for k in d:
if d[k] == v:
return k
raise LookupError()
Essa função é mais um exemplo do padrão de busca, mas usa um recurso que ainda não tínhamos visto: raise. A instrução raise causa uma exceção; neste caso, causa um LookupError, que é uma exceção integrada, usada para indicar que uma operação de busca falhou.
Se chegarmos ao fim do loop significa que v não aparece no dicionário como um valor, portanto apresentaremos uma exceção.
Aqui está um exemplo de uma busca reversa bem sucedida:
>>> h = histogram('parrot')
>>> k = reverse_lookup(h, 2)
>>> k
'r'
E uma mal sucedida:
>>> k = reverse_lookup(h, 3)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "<stdin>", line 5, in reverse_lookup
LookupError
O efeito causado por você ao apresentar uma exceção é igual ao causado pelo Python quando faz o mesmo: ele exibe um traceback e uma mensagem de erro.
A instrução raise pode receber uma mensagem de erro detalhada como argumento opcional. Por exemplo:
>>> raise LookupError('value does not appear in the dictionary')
Traceback (most recent call last):
File "<stdin>", line 1, in ?
LookupError: value does not appear in the dictionary
Uma busca reversa é muito mais lenta que uma busca no sentido normal; se for preciso fazê-lo muitas vezes, ou se o dicionário ficar muito grande, o desempenho do seu programa será prejudicado.
11.5 - Dicionários e listas
As listas podem aparecer como valores em um dicionário. Por exemplo, se você receber um dicionário que mapeie letras e frequências, é uma boa ideia invertê-lo; isto é, crie um dicionário que mapeie de frequências a letras. Como pode haver várias letras com a mesma frequência, cada valor no dicionário invertido deve ser uma lista de letras.
Aqui está uma função que inverte um dicionário:
def invert_dict(d):
inverse = dict()
for key in d:
val = d[key]
if val not in inverse:
inverse[val] = [key]
else:
inverse[val].append(key)
return inverse
Cada vez que o programa passar pelo loop, a key recebe uma chave de d e val recebe o valor correspondente. Se val não estiver em inverse significa que não foi vista antes, então criamos um item e o inicializamos com um item avulso (em inglês, singleton, uma lista que contém um único elemento). Se não for o caso é porque vimos esse valor antes, então acrescentamos a chave correspondente à lista.
Aqui está um exemplo:
>>> hist = histogram('parrot')
>>> hist
{'a': 1, 'p': 1, 'r': 2, 't': 1, 'o': 1}
>>> inverse = invert_dict(hist)
>>> inverse
{1: ['a', 'p', 't', 'o'], 2: ['r']}
A Figura 11.1 é um diagrama de estado mostrando hist e inverse. Um dicionário é representado como uma caixa com o tipo dict acima dela e os pares chave-valor no interior. Se os valores forem números inteiros, de ponto flutuante ou strings, desenho-os dentro da caixa, mas normalmente prefiro desenhar listas do lado de fora, para manter o diagrama simples.
 .
.
Figura 11.1 – Diagrama de estado de um dicionário e seu inverso.
As listas podem ser valores em um dicionário, como mostra este exemplo, mas não podem ser chaves. Isso é o que acontece se você tentar:
>>> t = [1, 2, 3]
>>> d = dict()
>>> d[t] = 'oops'
Traceback (most recent call last):
File "<stdin>", line 1, in ?
TypeError: list objects are unhashable
Já mencionei que um dicionário é implementado usando uma hashtable e isso significa que é preciso que as chaves possam ser hashable (que seja possível computar seu hash, e que este valor de hash seja imutável).
hash é uma função que recebe um valor (de qualquer tipo) e devolve um número inteiro. Dicionários usam esses números inteiros, chamados valores hash, para guardar e buscar pares chave-valor.
Este sistema funciona perfeitamente se as chaves forem imutáveis. Porém, se as chaves são mutáveis, como listas, coisas ruins acontecem. Por exemplo, quando você cria um par chave-valor, o Python guarda a chave na posição correspondente. Se você modificar a chave e então guardá-la novamente, ela iria para uma posição diferente. Nesse caso, você poderia ter duas entradas para a mesma chave, ou pode não conseguir encontrar uma chave. De qualquer forma, o dicionário não funcionaria corretamente.
É por isso que as chaves têm de ser hashable, e tipos mutáveis como listas, não são. A forma mais simples de resolver esta limitação é usar tuplas, que serão vistas no próximo capítulo.
Como os dicionários são mutáveis, eles não podem ser usados como chaves, mas podem ser usados como valores.
11.6 - Memos
Se usou a função de fibonacci em “Mais um exemplo”, na página 101, pode ter notado que quanto maior o argumento dado mais tempo a função leva para ser executada. Além disso, o tempo de execução aumenta rapidamente.
Para entender por que, considere a Figura 11.2, que mostra o gráfico de chamada de fibonacci com n=4.
 .
.
Figura 11.2 – Gráfico de chamada para fibonacci.
Um gráfico de chamada mostra um conjunto de frames de função, com linhas que unem cada frame aos frames das funções que chama. Na parte de cima do gráfico, fibonacci com n=4 chama fibonacci com n=3 e n=2. Por sua vez, fibonacci com n=3 chama fibonacci com n=2 e n=1. E assim por diante.
Conte quantas vezes fibonacci(0) e fibonacci(1) são chamadas. Essa é uma solução ineficiente para o problema, e piora conforme o argumento se torna maior.
Uma solução é acompanhar os valores que já foram calculados, guardando-os em um dicionário. Um valor calculado anteriormente que é guardado para uso posterior é chamado de memo. Aqui está uma versão com memos de fibonacci:
known = {0:0, 1:1}
def fibonacci(n):
if n in known:
return known[n]
res = fibonacci(n-1) + fibonacci(n-2)
known[n] = res
return res
known é um dicionário que monitora os números de Fibonacci que já conhecemos. Começa com dois itens: 0 mapeia a 0 e 1 mapeia a 1.
Sempre que fibonacci é chamada, ela verifica known. Se o resultado já estiver lá, pode voltar imediatamente. Se não for o caso, é preciso calcular o novo valor, acrescentá-lo ao dicionário e devolvê-lo.
Se você executar essa versão de fibonacci e a comparar com a original, descobrirá que é muito mais rápida.
11.7 - Variáveis globais
No exemplo anterior, known é criada fora da função, então pertence ao frame especial chamado __main__. As variáveis em __main__ às vezes são chamadas de globais, porque podem ser acessadas de qualquer função. Em contraste com as variáveis locais, que desaparecem quando sua função termina, as variáveis globais persistem de uma chamada da função à seguinte.
É comum usar variáveis globais para flags; isto é, variáveis booleanas que indicam (“flag”) se uma condição é verdadeira. Por exemplo, alguns programas usam um flag denominado verbose para controlar o nível de detalhe da saída:
verbose = True
def example1():
if verbose:
print('Running example1')
Se tentar reatribuir uma variável global, você pode se surpreender. O próximo exemplo mostra como acompanhar se a função foi chamada:
been_called = False
def example2():
been_called = True # ERRADO
Porém, se executá-la, você verá que o valor de been_called não se altera. O problema é que example2 cria uma nova variável local chamada been_called. A variável local some quando a função termina e não tem efeito sobre a variável global.
Para reatribuir uma variável global dentro de uma função é preciso declarar a variável como global antes de usá-la:
been_called = False
def example2():
global been_called
been_called = True
A instrução global diz ao interpretador algo como “Nesta função, quando digo been_called, estou falando da variável global; não crie uma local”.
Aqui está um exemplo que tenta atualizar uma variável global:
count = 0
def example3():
count = count + 1 # ERRADO
Se executá-la, você recebe:
UnboundLocalError: local variable 'count' referenced before assignment
O Python supõe que count seja local, e dentro desta suposição, a variável está sendo lida antes de ser escrita. A solução, mais uma vez, é declarar count como global:
def example3():
global count
count += 1
Se uma variável global se referir a um valor mutável, você pode alterar o valor sem declarar a variável:
known = {0:0, 1:1}
def example4():
known[2] = 1
Então você pode adicionar, retirar e substituir elementos de uma lista global ou dicionário, mas se quiser reatribuir a variável, precisa declará-la:
def example5():
global known
known = dict()
As variáveis globais podem ser úteis, mas se você tiver muitas delas e alterá-las com frequência, isso poderá dificultar a depuração do programa.
11.8 - Depuração
Ao trabalhar com conjuntos de dados maiores, depurar exibindo e verificando a saída à mão pode ser trabalhoso. Aqui estão algumas sugestões para depurar grandes conjuntos de dados:
Reduza a entrada
Se for possível, reduza o tamanho do conjunto de dados. Por exemplo, se o programa lê um arquivo de texto, comece com apenas as 10 primeiras linhas, ou com o menor exemplo que puder encontrar. Você pode editar os próprios arquivos ou alterar o programa para que leia só as primeiras n linhas (é melhor).
Se houver um erro, você pode reduzir n ao menor valor que manifeste o erro, e então aumentá-lo gradativamente até encontrar e corrigir o erro.
Verifique os resumos e tipos
Em vez de imprimir e verificar o conjunto de dados inteiro, pense em exibir resumos dos dados: por exemplo, o número de itens em um dicionário ou o total de uma lista de números.
Uma causa comum de erros em tempo de execução são valores de tipo incompatível. Para depurar essa espécie de erro, muitas vezes basta exibir o tipo de um valor.
Crie autoverificações
É possível escrever o código para verificar erros automaticamente. Por exemplo, se estiver calculando a média de uma lista de números, você pode verificar se o resultado não é mais alto que o maior elemento da lista ou mais baixo que o menor. Isso é chamado de “verificação de sanidade” porque descobre resultados “insanos”.
Outro tipo de verificação compara os resultados de dois cálculos diferentes para ver se são consistentes. Isso é chamado de “verificação de consistência”.
Formate a saída
A formatação da saída para depuração pode facilitar a busca de erros. Vimos um exemplo em “Depuração”, na página 172. O módulo pprint apresenta uma função pprint que exibe tipos integrados em um formato mais legível para humanos (pprint é a abreviação de “pretty print” (bela exibição)).
Reforçando, o tempo que você passar construindo o scaffolding (o andaime) pode reduzir o tempo de depuração.
11.9 - Glossário
mapeamento
Relação na qual cada elemento de um conjunto corresponde a um elemento de outro conjunto.
dicionário
Mapeamento de chaves aos seus valores correspondentes.
par chave-valor
Representação do mapeamento de uma chave a um valor.
item
Em um dicionário, outro nome para um par chave-valor.
chave
Objeto que aparece em um dicionário como a primeira parte de um par chave-valor.
valor
Objeto que aparece em um dicionário como a segunda parte de um par chave-valor. Isso é mais específico que o nosso uso anterior da palavra “valor”.
implementação
Uma forma de executar um cálculo.
hashtable
Algoritmo usado para implementar dicionários de Python.
função hash
Função usada por uma hashtable para calcular a posição de uma chave.
hashable
Um tipo que tem uma função hash. Tipos imutáveis como números inteiros, de ponto flutuante e strings são hashable; tipos mutáveis, como listas e dicionários, não são.
busca
Operação de dicionário que recebe uma chave e encontra o valor correspondente.
busca reversa
Operação de dicionário que recebe um valor e encontra uma ou várias chaves que o mapeiem.
instrução raise
Instrução que (deliberadamente) causa uma exceção.
item avulso (singleton)
Uma lista (ou outra sequência) com um único elemento.
gráfico de chamada
Um diagrama que mostra cada frame criado durante a execução de um programa, com uma flecha apontando quem chama a quem é chamado.
memo
Valor já calculado, guardado para não ter que fazer o mesmo cálculo no futuro.
variável global
Variável definida fora de uma função. As variáveis globais podem ser acessadas de qualquer função.
instrução global
Instrução que declara um nome de variável global.
flag
Variável booleana usada para indicar se uma condição é verdadeira.
declaração
Instrução tal como global, que diz ao interpretador algo a respeito de uma variável.
11.10 - Exercícios
Exercício 11.1
Escreva uma função que leia as palavras em words.txt e guarde-as como chaves em um dicionário. Não importa quais são os valores. Então você pode usar o operador in como uma forma rápida de verificar se uma string está no dicionário.
Se fez o Exercício 10.10, você pode comparar a velocidade desta implementação com o operador in de listas e a busca por bisseção.
Exercício 11.2
Leia a documentação do método de dicionário setdefault e use-o para escrever uma versão mais concisa de invert_dict.
Solução: http://thinkpython2.com/code/invert_dict.py.
Exercício 11.3
Memorize a função de Ackermann do Exercício 6.2 e veja se a memorização permite avaliar a função com argumentos maiores. Dica: não.
Solução: http://thinkpython2.com/code/ackermann_memo.py.
Exercício 11.4
Se fez o Exercício 10.7, você já tem uma função chamada has_duplicates, que recebe uma lista como parâmetro e retorna True se houver algum objeto que aparece mais de uma vez na lista.
Use um dicionário para escrever uma versão mais rápida e simples de has_duplicates.
Solução: http://thinkpython2.com/code/has_duplicates.py.
Exercício 11.5
Duas palavras são “pares rotacionados” se for possível rotacionar um deles e chegar ao outro (ver rotate_word no Exercício 8.5).
Escreva um programa que leia uma lista de palavras e encontre todos os pares rotacionados.
Solução: http://thinkpython2.com/code/rotate_pairs.py.
Exercício 11.6
Aqui está outro quebra-cabeça do programa Car Talk (http://www.cartalk.com/content/puzzlers):
Ele foi enviado por Dan O’Leary. Dan descobriu uma palavra comum, com uma sílaba e cinco letras que tem a seguinte propriedade única. Ao removermos a primeira letra, as letras restantes formam um homófono da palavra original, que é uma palavra que soa exatamente da mesma forma. Substitua a primeira letra, isto é, coloque-a de volta, retire a segunda letra e o resultado é um outro homófono da palavra original. E a pergunta é, qual é a palavra?
Agora vou dar um exemplo que não funciona. Vamos usar a palavra de cinco letras, ‘wrack’ (mover, eliminar). W-R-A-C-K, como na expressão ‘wrack with pain’ (se contorcer de dor). Se eu retirar a primeira letra, sobra uma palavra de quatro letras, ‘R-A-C-K’ (galhada). Como na frase, ‘Holy cow, did you see the rack on that buck! It must have been a nine-pointer!’ (‘Minha nossa, você viu a galhada daquele cervo! Deve ter nove pontas!’). É um homófono perfeito. Se puser o ‘w’ de volta e retirar o ‘r’ em vez disso, sobra a palavra ‘wack’, que é uma palavra de verdade, mas não é um homófono das outras duas palavras.
Mas há pelo menos uma palavra que Dan e eu conhecemos, que produz dois homófonos se você retirar qualquer uma das duas primeiras letras, e duas novas palavras de quatro letras são formadas. A pergunta é, qual é a palavra?
Você pode usar o dicionário do Exercício 11.1 para verificar se uma string está na lista de palavras.
Para verificar se duas palavras são homófonas, você pode usar o Dicionário de pronúncia CMU. Ele pode ser baixado em http://www.speech.cs.cmu.edu/cgi-bin/cmudict ou em http://thinkpython2.com/code/c06d. Você também pode baixar http://thinkpython2.com/code/pronounce.py, que tem uma função chamada read_dictionary, que lê o dicionário de pronúncia e retorna um dicionário de Python que mapeia cada palavra a uma string que descreve sua pronúncia primária.
Escreva um programa que liste todas as palavras que resolvem o quebra-cabeça.
Solução: http://thinkpython2.com/code/homophone.py.
Capítulo 12: Tuplas
Este capítulo apresenta mais um tipo integrado, a tupla, e descreve como as listas, os dicionários e as tuplas trabalham juntos. Além disso, apresento um recurso útil para listas de argumentos de comprimento variável: os operadores gather e scatter.
Uma observação: não há consenso sobre como pronunciar “tuple” (em inglês). Algumas pessoas dizem “tuhple”, que rima com “supple”. Porém, no contexto da programação, a maioria das pessoas diz “too-ple”, que rima com “quadruple”.
12.1 - Tuplas são imutáveis
Uma tupla é uma sequência de valores. Os valores podem ser de qualquer tipo, e podem ser indexados por números inteiros, portanto, nesse sentido, as tuplas são muito parecidas com as listas. A diferença importante é que as tuplas são imutáveis.
Sintaticamente, uma tupla é uma lista de valores separados por vírgulas:
>>> t = 'a', 'b', 'c', 'd', 'e'
Embora não seja sempre necessário, é comum colocar tuplas entre parênteses:
>>> t = ('a', 'b', 'c', 'd', 'e')
Para criar uma tupla com um único elemento, é preciso incluir uma vírgula final:
>>> t1 = 'a',
>>> type(t1)
<class 'tuple'>
Um único valor entre parênteses não é uma tupla:
>>> t2 = ('a')
>>> type(t2)
<class 'str'>
Outra forma de criar uma tupla é com a função integrada tuple. Sem argumentos, cria uma tupla vazia:
>>> t = tuple()
>>> t
()
Se os argumentos forem uma sequência (string, lista ou tupla), o resultado é uma tupla com os elementos da sequência:
>>> t = tuple('lupins')
>>> t
('l', 'u', 'p', 'i', 'n', 's')
Como tuple é o nome de uma função integrada, você deve evitar usá-lo como nome de variável.
A maior parte dos operadores de lista também funciona em tuplas. O operador de colchetes indexa um elemento:
>>> t = ('a', 'b', 'c', 'd', 'e')
>>> t[0]
'a'
E o operador de fatia seleciona vários elementos:
>>> t[1:3]
('b', 'c')
Entretanto, se tentar alterar um dos elementos da tupla, vai receber um erro:
>>> t[0] = 'A'
TypeError: object doesn't support item assignment
Como tuplas são imutáveis, você não pode alterar os elementos, mas pode substituir uma tupla por outra:
>>> t = ('A') + t[1:]
>>> t
('A', 'b', 'c', 'd', 'e')
Essa instrução faz uma nova tupla e então a atribui a t.
Os operadores relacionais funcionam com tuplas e outras sequências; o Python começa comparando o primeiro elemento de cada sequência. Se forem iguais, vai para os próximos elementos, e assim por diante, até que encontre elementos que sejam diferentes. Os elementos subsequentes não são considerados (mesmo se forem muito grandes).
>>> (0, 1, 2) < (0, 3, 4)
True
>>> (0, 1, 2000000) < (0, 3, 4)
True
12.2 - Atribuição de tuplas
Muitas vezes, é útil trocar os valores de duas variáveis. Com a atribuição convencional, é preciso usar uma variável temporária. Por exemplo, trocar a e b.
>>> temp = a
>>> a = b
>>> b = temp
Essa solução é trabalhosa; a atribuição de tuplas é mais elegante:
>>> a, b = b, a
O lado esquerdo é uma tupla de variáveis; o lado direito é uma tupla de expressões. Cada valor é atribuído à sua respectiva variável. Todas as expressões no lado direito são avaliadas antes de todas as atribuições.
O número de variáveis à esquerda e o número de valores à direita precisam ser iguais:
>>> a, b = 1, 2, 3
ValueError: too many values to unpack
De forma geral, o lado direito pode ter qualquer tipo de sequência (string, lista ou tupla). Por exemplo, para dividir um endereço de email em um nome de usuário e um domínio, você poderia escrever:
>>> addr = 'monty@python.org'
>>> uname, domain = addr.split('@')
O valor de retorno do split é uma lista com dois elementos; o primeiro elemento é atribuído a uname, o segundo a domain:
>>> uname
'monty'
>>> domain
'python.org'
12.3 - Tuplas como valores de retorno
Falando estritamente, uma função só pode retornar um valor, mas se o valor for uma tupla, o efeito é o mesmo que retornar valores múltiplos. Por exemplo, se você quiser dividir dois números inteiros e calcular o quociente e resto, não é eficiente calcular x/y e depois x%y. É melhor calcular ambos ao mesmo tempo.
A função integrada divmod toma dois argumentos e devolve uma tupla de dois valores: o quociente e o resto. Você pode guardar o resultado como uma tupla:
>>> t = divmod(7, 3)
>>> t
(2, 1)
Ou usar a atribuição de tuplas para guardar os elementos separadamente:
>>> quot, rem = divmod(7, 3)
>>> quot
2
>>> rem
1
Aqui está um exemplo de função que retorna uma tupla:
def min_max(t):
return min(t), max(t)
max e min são funções integradas que encontram os maiores e menores elementos de uma sequência. min_max calcula ambos e retorna uma tupla de dois valores.
12.4 - Tuplas com argumentos de comprimento variável
As funções podem receber um número variável de argumentos. Um nome de parâmetro que comece com * reúne vários argumentos em uma tupla. Por exemplo, printall recebe qualquer número de argumentos e os exibe:
def printall(*args):
print(args)
O parâmetro com o prefixo * pode ter qualquer nome que você goste, mas args é o convencional. É assim que a função funciona:
>>> printall(1, 2.0, '3')
(1, 2.0, '3')
O complemento de reunir é espalhar. Se você tiver uma sequência de valores e quiser passá-la a uma função como argumentos múltiplos, pode usar o operador *. Por exemplo, o divmod recebe exatamente dois argumentos; ele não funciona com uma tupla:
>>> t = (7, 3)
>>> divmod(t)
TypeError: divmod expected 2 arguments, got 1
No entanto, se você espalhar a tupla, aí funciona:
>>> divmod(*t)
(2, 1)
Muitas das funções integradas usam tuplas com argumentos de comprimento variável. Por exemplo, max e min podem receber qualquer número de argumentos:
>>> max(1, 2, 3)
3
Mas sum, não:
>>> sum(1, 2, 3)
TypeError: sum expected at most 2 arguments, got 3
Como exercício, escreva uma função chamada sumall que receba qualquer número de argumentos e retorne a soma deles.
12.5 - Listas e tuplas
zip é uma função integrada que recebe duas ou mais sequências e devolve uma lista de tuplas onde cada tupla contém um elemento de cada sequência. O nome da função tem a ver com o zíper, que se junta e encaixa duas carreiras de dentes.
Este exemplo encaixa uma string e uma lista:
>>> s = 'abc'
>>> t = [0, 1, 2]
>>> zip(s, t)
<zip object at 0x7f7d0a9e7c48>
O resultado é um objeto zip que sabe como percorrer os pares. O uso mais comum de zip é em um loop for:
>>> for pair in zip(s, t):
... print(pair)
...
('a', 0)
('b', 1)
('c', 2)
Um objeto zip é um tipo de iterador, ou seja, qualquer objeto que percorre ou itera sobre uma sequência. Iteradores são semelhantes a listas em alguns aspectos, mas, ao contrário de listas, não é possível usar um índice para selecionar um elemento de um iterador.
Se quiser usar operadores e métodos de lista, você pode usar um objeto zip para fazer uma lista:
>>> list(zip(s, t))
[('a', 0), ('b', 1), ('c', 2)]
O resultado é uma lista de tuplas; neste exemplo, cada tupla contém um caractere da string e o elemento correspondente da lista.
Se as sequências não forem do mesmo comprimento, o resultado tem o comprimento da mais curta:
>>> list(zip('Anne', 'Elk'))
[('A', 'E'), ('n', 'l'), ('n', 'k')]
Você pode usar a atribuição de tuplas em um loop for para atravessar uma lista de tuplas:
t = [('a', 0), ('b', 1), ('c', 2)]
for letter, number in t:
print(number, letter)
Cada vez que o programa passa pelo loop, o Python seleciona a próxima tupla na lista e atribui os elementos letter e number. A saída deste loop é:
0 a
1 b
2 c
Se combinar zip, for e atribuição de tuplas, você pode fazer uma expressão útil para percorrer duas (ou mais) sequências ao mesmo tempo. Por exemplo, has_match recebe duas sequências, t1 e t2 e retorna True se houver um índice i tal que t1[i] == t2[i]:
def has_match(t1, t2):
for x, y in zip(t1, t2):
if x == y:
return True
return False
Se precisar atravessar os elementos de uma sequência e seus índices, você pode usar a função integrada enumerate:
for index, element in enumerate('abc'):
print(index, element)
O resultado de enumerate é um objeto enumerate, que itera sobre uma sequência de pares; cada par contém um índice (começando de 0) e um elemento da sequência dada. Neste exemplo, a saída é
0 a
1 b
2 c
De novo.
12.6 - Dicionários e tuplas
Os dicionários têm um método chamado items que devolve uma sequência de tuplas, onde cada tupla é um par chave-valor:
>>> d = {'a':0, 'b':1, 'c':2}
>>> t = d.items()
>>> t
dict_items([('c', 2), ('a', 0), ('b', 1)])
O resultado é um objeto dict_items, que é um iterador que percorre os pares chave-valor. Você pode usá-lo em um loop for, desta forma:
>>> for key, value in d.items():
... print(key, value)
...
c 2
a 0
b 1
Como se poderia esperar de um dicionário, os itens não estão em nenhuma ordem em particular.
Indo em outra direção, você pode usar uma lista de tuplas para inicializar um novo dicionário:
>>> t = [('a', 0), ('c', 2), ('b', 1)]
>>> d = dict(t)
>>> d
{'a': 0, 'c': 2, 'b': 1}
Combinar dict com zip produz uma forma concisa de criar um dicionário:
>>> d = dict(zip('abc', range(3)))
>>> d
{'a': 0, 'c': 2, 'b': 1}
O método de dicionário update também recebe uma lista de tuplas e as adiciona, como pares chave-valor, a um dicionário existente.
É comum usar tuplas como chaves em dicionários (principalmente porque você não pode usar listas). Por exemplo, uma lista telefônica poderia mapear pares de sobrenome e primeiro nome a números de telefone. Supondo que tenhamos definido last, first e number, podemos escrever:
directory[last, first] = number
A expressão entre chaves é uma tupla. Podemos usar atribuição de tuplas para atravessar este dicionário:
for last, first in directory:
print(first, last, directory[last,first])
Este loop atravessa as chaves em directory, que são tuplas. Ele atribui os elementos de cada tupla para last e first, e então exibe o nome e número de telefone correspondente.
Há duas formas de representar tuplas em um diagrama de estado. A versão mais detalhada mostra os índices e elementos como aparecem em uma lista. Por exemplo, a tupla ('Cleese', 'John') apareceria como na Figura 12.1.
 .
.
Figura 12.1 – Diagrama de estado de uma tupla.
No entanto, em um diagrama maior, você pode querer omitir os detalhes. Por exemplo, um diagrama da lista telefônica poderia ser como o da Figura 12.2.
 .
.
Figura 12.2 – Diagrama de estado de um dicionário com chaves do tipo tupla.
Aqui as tuplas são mostradas usando a sintaxe do Python para simplificar o gráfico. O número de telefone no diagrama é a linha de reclamações da BBC, então, por favor, não ligue para lá.
12.7 - Sequências de sequências
Eu me concentrei em listas de tuplas, mas quase todos os exemplos neste capítulo também funcionam com listas de listas, tuplas de tuplas e tuplas de listas. Para evitar enumerar as combinações possíveis, às vezes é mais fácil falar sobre sequências de sequências.
Em muitos contextos, os tipos diferentes de sequências (strings, listas e tuplas) podem ser usados de forma intercambiável. Então, como escolher uma em vez da outra?
Para começar com o óbvio, as strings são mais limitadas que outras sequências porque os elementos têm de ser caracteres. Também são imutáveis. Se precisar da capacidade de alterar caracteres em uma string (em vez de criar outra string) você pode querer usar uma lista de caracteres.
As listas são mais comuns que as tuplas, principalmente porque são mutáveis. Mas há alguns casos em que você pode preferir tuplas:
-
Em alguns contextos, como em uma instrução
return, é sintaticamente mais simples criar uma tupla que uma lista. -
Se quiser usar uma sequência como uma chave de dicionário, é preciso usar um tipo imutável como uma tupla ou string.
-
Se estiver passando uma sequência como um argumento a uma função, usar tuplas reduz o potencial de comportamento inesperado devido a alias.
Como tuplas são imutáveis, elas não fornecem métodos como sort e reverse, que alteram listas existentes. Porém, o Python fornece a função integrada sorted, que recebe qualquer sequência e retorna uma nova lista com os mesmos elementos ordenados, e reversed, que recebe uma sequência e retorna um iterador que percorre a lista em ordem reversa.
12.8 - Depuração
As listas, os dicionários e as tuplas são exemplos de estruturas de dados; neste capítulo estamos começando a ver estruturas de dados compostas, como as listas de tuplas ou dicionários que contêm tuplas como chaves e listas como valores. As estruturas de dados compostas são úteis, mas são propensas ao que chamo de erros de forma; isto é, erros causados quando uma estrutura de dados tem o tipo, tamanho ou estrutura incorretos. Por exemplo, se você estiver esperando uma lista com um número inteiro e eu der apenas o número inteiro (não em uma lista), não vai funcionar.
Para ajudar a depurar esses tipos de erro, escrevi um módulo chamado structshape, que fornece uma função, também chamada structshape, que recebe qualquer tipo de estrutura de dados como argumento e retorna uma string, que resume sua forma. Você pode baixá-la em http://thinkpython2.com/code/structshape.py.
Aqui está o resultado de uma lista simples:
>>> from structshape import structshape
>>> t = [1, 2, 3]
>>> structshape(t)
'list of 3 int'
Um programa mais sofisticado pode escrever “list of 3 ints”, mas é mais fácil não lidar com plurais. Aqui está uma lista de listas:
>>> t2 = [[1,2], [3,4], [5,6]]
>>> structshape(t2)
'list of 3 list of 2 int'
Se os elementos da lista não forem do mesmo tipo, structshape os agrupa, na ordem, por tipo:
>>> t3 = [1, 2, 3, 4.0, '5', '6', [7], [8], 9]
>>> structshape(t3)
'list of (3 int, float, 2 str, 2 list of int, int)'
Aqui está uma lista de tuplas:
>>> s = 'abc'
>>> lt = list(zip(t, s))
>>> structshape(lt)
'list of 3 tuple of (int, str)'
E aqui está um dicionário com três itens que mapeia números inteiros a strings:
>>> d = dict(lt)
>>> structshape(d)
'dict of 3 int->str'
Se estiver com problemas para monitorar suas estruturas de dados, o structshape pode ajudar.
12.9 - Glossário
tupla
Sequência imutável de elementos.
atribuição de tupla
Atribuição com uma sequência no lado direito e uma tupla de variáveis à esquerda. O lado direito é avaliado e então seus elementos são atribuídos às variáveis à esquerda.
gather
Operação para montar uma tupla com argumento de comprimento variável.
scatter
Operação para tratar uma sequência como uma lista de argumentos.
objeto zip
O resultado de chamar uma função integrada zip; um objeto que se repete por uma sequência de tuplas.
iterador
Objeto que pode se repetir por uma sequência, mas que não oferece operadores de lista e métodos.
estrutura de dados
Coleção de valores relacionados, muitas vezes organizados em listas, dicionários, tuplas etc.
erro de forma
Erro causado pelo fato de o valor ter a forma incorreta; isto é, tipo ou tamanho incorreto.
12.10 - Exercícios
Exercício 12.1
Escreva uma função chamada most_frequent que receba uma string e exiba as letras em ordem decrescente de frequência. Encontre amostras de texto de vários idiomas diferentes e veja como a frequência das letras varia entre os idiomas. Compare seus resultados com as tabelas em http://en.wikipedia.org/wiki/Letter_frequencies.
Solução: http://thinkpython2.com/code/most_frequent.py.
Exercício 12.2
Mais anagramas!
- Escreva um programa que leia uma lista de palavras de um arquivo (veja “Leitura de listas de palavras”, na página 133) e imprima todos os conjuntos de palavras que são anagramas.
Aqui está um exemplo de como a saída pode parecer:
['deltas', 'desalt', 'lasted', 'salted', 'slated', 'staled']
['retainers', 'ternaries']
['generating', 'greatening']
['resmelts', 'smelters', 'termless']
Dica: você pode querer construir um dicionário que mapeie uma coleção de letras a uma lista de palavras que podem ser soletradas com essas letras. A pergunta é: como representar a coleção de letras de forma que possa ser usada como uma chave?
-
Altere o programa anterior para que exiba a lista mais longa de anagramas primeiro, seguido pela segunda mais longa, e assim por diante.
-
No Scrabble, um “bingo” é quando você joga todas as sete peças na sua estante, junto com uma peça no tabuleiro, para formar uma palavra de oito letras. Que coleção de oito letras forma o maior número possível de bingos? Dica: há sete.
Solução: http://thinkpython2.com/code/anagram_sets.py.
Exercício 12.3
Duas palavras formam um “par de metátese” se você puder transformar uma na outra trocando duas letras, por exemplo, “converse” e “conserve”. Escreva um programa que descubra todos os pares de metátese no dicionário. Dica: não teste todos os pares de palavras e não teste todas as trocas possíveis.
Solução: http://thinkpython2.com/code/metathesis.py. Crédito: este exercício foi inspirado por um exemplo em http://puzzlers.org.
Exercício 12.4
Aqui está outro quebra-cabeça do programa Car Talk (http://www.cartalk.com/content/puzzlers):
Qual é a palavra inglesa mais longa, que permanece uma palavra inglesa válida, conforme vai removendo suas letras, uma após a outra?
Agora, as letras podem ser retiradas do fim ou do meio, mas você não pode reajustar nenhuma delas. Cada vez que remove uma letra, você acaba com outra palavra inglesa. Se fizer isto, eventualmente você acabará com uma letra e isso também será uma palavra inglesa; uma encontrada no dicionário. Quero saber qual é a palavra mais longa e quantas letras tem?
Vou dar um pequeno exemplo modesto: Sprite. Ok? Você começa com sprite, tira uma letra do interior da palavra, tira o r, e ficamos com a palavra spite, então tiramos o e do fim, ficamos com spit, tiramos o s, ficamos com pit, it e I.
Escreva um programa que encontre todas as palavras que podem ser reduzidas desta forma, e então encontre a mais longa.
Este exercício é um pouco mais desafiador que a maioria, então aqui estão algumas sugestões:
-
Você pode querer escrever uma função que receba uma palavra e calcule uma lista de todas as palavras que podem ser formadas retirando uma letra. Esses são os “filhos” da palavra.
-
Recursivamente, uma palavra é redutível se algum de seus filhos for redutível. Como caso base, você pode considerar a string vazia redutível.
-
A lista de palavras que forneci, words.txt, não contém palavras de uma letra só. Portanto, você pode querer acrescentar “I”, “a”, e a string vazia.
-
Para melhorar o desempenho do seu programa, você pode querer memorizar as palavras conhecidas por serem redutíveis.
Solução: http://thinkpython2.com/code/reducible.py.
Capítulo 13: Estudo de caso: seleção de estrutura de dados
Neste ponto você já aprendeu sobre as principais estruturas de dados do Python, e viu alguns algoritmos que as usam. Se quiser saber mais sobre algoritmos, pode ler o Capítulo 21. Mas isso não é necessário para continuar, pode lê-lo a qualquer momento em que tenha interesse.
Este capítulo apresenta um estudo de caso com exercícios que fazem pensar sobre a escolha de estruturas de dados e práticas de uso delas.
13.1 - Análise de frequência de palavras
Como de hábito, você deve pelo menos tentar fazer os exercícios antes de ler as minhas soluções.
Exercício 13.1
Escreva um programa que leia um arquivo, quebre cada linha em palavras, remova os espaços em branco e a pontuação das palavras, e as converta em letras minúsculas.
Dica: O módulo string oferece uma string chamada whitespace, que contém espaço, tab, newline etc., e punctuation, que contém os caracteres de pontuação. Vamos ver se conseguimos fazer o Python falar palavrões:
>>> import string
>>> string.punctuation
'!"#$%&\'()*+,-./:;<=>?@[\]^_`{|}~'
Além disso, você pode usar os métodos de string, strip, replace e translate.
Exercício 13.2
Acesse o Projeto Gutenberg (https://gutenberg.org) e baixe seu livro favorito em domínio público em formato de texto simples.
Altere seu programa do exercício anterior para ler o livro que você baixou, pulando as informações do cabeçalho no início do arquivo e processando o resto das palavras como antes.
Então altere o programa para contar o número total de palavras no livro e o número de vezes que cada palavra é usada.
Exiba o número de palavras diferentes usadas no livro. Compare livros diferentes de autores diferentes, escritos em eras diferentes. Que autor usa o vocabulário mais extenso?
Exercício 13.3
Altere o programa do exercício anterior para exibir as 20 palavras mais frequentes do livro.
Exercício 13.4
Altere o programa anterior para ler uma lista de palavras (ver “Leitura de listas de palavras”, na página 133) e então exiba todas as palavras do livro que não estão na lista de palavras. Quantas delas são erros ortográficos? Quantas delas são palavras comuns que deveriam estar na lista de palavras, e quantas são muito obscuras?
13.2 - Números aleatórios
Com as mesmas entradas, a maior parte dos programas gera as mesmas saídas a cada vez, então eles são chamados de deterministas. Determinismo normalmente é uma coisa boa, já que esperamos que o mesmo cálculo produza o mesmo resultado. Para algumas aplicações, entretanto, queremos que o computador seja imprevisível. Os jogos são um exemplo óbvio, mas há outros.
Fazer um programa não determinista de verdade é difícil; mas há formas de, pelo menos, fazê-los parecer que não são. Uma delas é usar algoritmos que geram números pseudoaleatórios. Os números pseudoaleatórios não são aleatórios mesmo porque são gerados por um cálculo determinista, mas é quase impossível distingui-los dos aleatórios só olhando para os números.
O módulo random fornece funções que geram números pseudoaleatórios (que chamarei apenas de “aleatórios” daqui em diante).
A função random retorna um número de ponto flutuante entre 0,0 e 1,0 (incluindo 0,0, mas não 1,0). Cada vez que random é chamada, você recebe o próximo número em uma longa série. Para ver uma amostra, execute este loop:
import random
for i in range(10):
x = random.random()
print(x)
A função randint recebe os parâmetros low e high e retorna um número inteiro entre low e high (inclusive ambos):
>>> random.randint(5, 10)
5
>>> random.randint(5, 10)
9
Para escolher aleatoriamente um elemento de uma sequência, você pode usar choice:
>>> t = [1, 2, 3]
>>> random.choice(t)
2
>>> random.choice(t)
3
O módulo random também fornece funções para gerar valores aleatórios de distribuições contínuas, incluindo gaussianas, exponenciais, gamma e algumas outras.
Exercício 13.5
Escreva uma função chamada choose_from_hist que receba um histograma como definido em “Um dicionário como uma coleção de contadores”, na página 163, e retorne um valor aleatório do histograma, escolhido por probabilidade em proporção à frequência. Por exemplo, para este histograma:
>>> t = ['a', 'a', 'b']
>>> hist = histogram(t)
>>> hist
{'a': 2, 'b': 1}
sua função deve retornar 'a' com a probabilidade de 2/3 e 'b' com a probabilidade 1/3.
13.3 - Histograma de palavras
É uma boa ideia tentar fazer os exercícios anteriores antes de continuar. Você pode baixar minha solução em http://thinkpython2.com/code/analyze_book1.py. Também vai precisar de http://thinkpython2.com/code/emma.txt.
Aqui está um programa que lê um arquivo e constrói um histograma das palavras no arquivo:
import string
def process_file(filename):
hist = dict()
fp = open(filename)
for line in fp:
process_line(line, hist)
return hist
def process_line(line, hist):
line = line.replace('-', ' ')
for word in line.split():
word = word.strip(string.punctuation + string.whitespace)
word = word.lower()
hist[word] = hist.get(word, 0) + 1
hist = process_file('emma.txt')
Este programa lê emma.txt, que contém o texto de Emma, de Jane Austen.
process_file faz o loop pelas linhas do arquivo, passando-as uma a uma para process_line. O histograma hist está sendo usado como um acumulador.
process_line usa o método de string replace para substituir hifens por espaços antes de usar split para quebrar a linha em uma lista de strings. Ele atravessa a lista de palavras e usa strip e lower para retirar a pontuação e converter tudo em letras minúsculas. (Dizer que as strings “são convertidas” é uma forma simples de explicar a coisa; lembre-se de que as strings são imutáveis, então métodos como strip e lower retornam novas strings)
Finalmente, process_line atualiza o histograma, criando um novo item ou incrementando um existente.
Para contar o número total de palavras no arquivo, podemos somar as frequências no histograma:
def total_words(hist):
return sum(hist.values())
O número de palavras diferentes é somente o número de itens no dicionário:
def different_words(hist):
return len(hist)
Aqui está o código para exibir os resultados:
print('Total number of words:', total_words(hist))
print('Number of different words:', different_words(hist))
E os resultados:
Total number of words: 161080
Number of different words: 7214
13.4 - Palavras mais comuns
Para encontrar as palavras mais comuns, podemos fazer uma lista de tuplas, onde cada tupla contenha uma palavra e a sua frequência, e ordenar a lista.
A função seguinte recebe um histograma e retorna uma lista de tuplas de palavras e frequências:
def most_common(hist):
t = []
for key, value in hist.items():
t.append((value, key))
t.sort(reverse=True)
return t
Em cada tupla, a frequência aparece primeiro, então a lista resultante é ordenada por frequência. Aqui está um loop que imprime as 10 palavras mais comuns:
t = most_common(hist)
print('The most common words are:')
for freq, word in t[:10]:
print(word, freq, sep='\\t')
Uso o argumento de palavra-chave sep para que print use um caractere tab como separador, em vez de um espaço, assim a segunda coluna fica alinhada verticalmente. Aqui estão os resultados de Emma:
The most common words are:
to 5242
the 5205
and 4897
of 4295
i 3191
a 3130
it 2529
her 2483
was 2400
she 2364
Este código pode ser simplificado usando o parâmetro key da função sort. Se tiver curiosidade, pode ler sobre ele em https://wiki.python.org/moin/HowTo/Sorting.
13.5 - Parâmetros opcionais
Vimos funções integradas e métodos que recebem argumentos opcionais. É possível escrever funções definidas pelos programadores com argumentos opcionais, também. Por exemplo, aqui está uma função que exibe as palavras mais comuns em um histograma:
def print_most_common(hist, num=10):
t = most_common(hist)
print('The most common words are:')
for freq, word in t[:num]:
print(word, freq, sep='\\t')
O primeiro parâmetro é necessário; o segundo é opcional. O valor padrão de num é 10.
Se você só fornecer um argumento:
print_most_common(hist)
num recebe o valor padrão. Se fornecer dois argumentos:
print_most_common(hist, 20)
num recebe o valor do argumento em vez disso. Em outras palavras, o argumento opcional ignora o valor padrão.
Se uma função tem ambos os parâmetros obrigatório e opcional, todos os parâmetros necessários têm que vir primeiro, seguidos pelos opcionais.
13.6 - Subtração de dicionário
Encontrar as palavras do livro que não estão na lista de palavras de words.txt é um problema que você pode reconhecer como subtração de conjuntos; isto é, queremos encontrar todas as palavras de um conjunto (as palavras no livro) que não estão no outro (as palavras na lista).
subtract recebe os dicionários d1 e d2 e devolve um novo dicionário que contém todas as chaves de d1 que não estão em d2. Como não nos preocupamos com os valores, estabelecemos todos como None:
def subtract(d1, d2):
res = dict()
for key in d1:
if key not in d2:
res[key] = None
return res
Para encontrar as palavras no livro que não estão em words.txt, podemos usar process_file para construir um histograma para words.txt, e então subtrair:
words = process_file('words.txt')
diff = subtract(hist, words)
print("Words in the book that aren't in the word list:")
for word in diff:
print(word, end=' ')
Aqui estão alguns resultados de Emma:
Words in the book that aren't in the word list:
rencontre jane's blanche woodhouses disingenuousness
friend's venice apartment ...
Algumas dessas palavras são nomes e possessivos. Os outros, como “rencontre”, já não são de uso comum. Mas algumas são palavras comuns que realmente deveriam estar na lista!
Exercício 13.6
O Python fornece uma estrutura de dados chamada set, que fornece muitas operações de conjunto. Você pode ler sobre elas em “Conjuntos”, na página 274, ou ler a documentação em http://docs.python.org/3/library/stdtypes.html#types-set.
Escreva um programa que use a subtração de conjuntos para encontrar palavras no livro que não estão na lista de palavras.
Solução: http://thinkpython2.com/code/analyze_book2.py.
13.7 - Palavras aleatórias
Para escolher uma palavra aleatória do histograma, o algoritmo mais simples é construir uma lista com várias cópias de cada palavra, segundo a frequência observada, e então escolher da lista:
def random_word(h):
t = []
for word, freq in h.items():
t.extend([word] * freq)
return random.choice(t)
A expressão [word] * freq cria uma lista com freq cópias da string word. O método extend é similar a append, exceto pelo argumento, que é uma sequência.
Esse algoritmo funciona, mas não é muito eficiente; cada vez que você escolhe uma palavra aleatória, ele reconstrói a lista, que é tão grande quanto o livro original. Uma melhoria óbvia é construir a lista uma vez e então fazer seleções múltiplas, mas a lista ainda é grande.
Uma alternativa é:
-
Usar
keyspara conseguir uma lista das palavras no livro. -
Construir uma lista que contenha a soma cumulativa das frequências das palavras (veja o Exercício 10.2). O último item desta lista é o número total de palavras no livro, n.
-
Escolher um número aleatório de 1 a n. Use uma pesquisa de bisseção (veja o Exercício 10.10) para encontrar o índice onde o número aleatório seria inserido na soma cumulativa.
-
Usar o índice para encontrar a palavra correspondente na lista de palavras.
Exercício 13.7
Escreva um programa que use este algoritmo para escolher uma palavra aleatória do livro.
Solução: http://thinkpython2.com/code/analyze_book3.py.
13.8 - Análise de Markov
Se escolher palavras do livro aleatoriamente, você pode até captar certo sentido a partir do vocabulário, mas provavelmente não vai conseguir uma sentença completa:
this the small regard harriet which knightley's it most things
Uma série de palavras aleatórias raramente faz sentido porque não há nenhuma relação entre palavras sucessivas. Por exemplo, em uma sentença de verdade você esperaria que um artigo como “o” fosse seguido de um adjetivo ou um substantivo, e provavelmente não um verbo ou advérbio.
Uma forma de medir estes tipos de relações é a análise de Markov, que caracteriza, para uma dada sequência de palavras, o que poderia vir a seguir, segundo a probabilidade. Por exemplo, a canção “Eric, the Half a Bee” começa assim:
Half a bee, philosophically,
Must, ipso facto, half not be.
But half the bee has got to be
Vis a vis, its entity. D’you see?
But can a bee be said to be
Or not to be an entire bee
When half the bee is not a bee
Due to some ancient injury?
Nesse texto, a frase “half the” sempre é seguida pela palavra “bee”, mas a frase “the bee” pode ser seguida por “has” ou “is”.
O resultado da análise de Markov é um mapeamento de cada prefixo (como “half the” e “the bee”) a todos os sufixos possíveis (como “has” e “is”).
Com este mapeamento você pode gerar um texto aleatório, começando com qualquer prefixo e escolhendo a esmo entre os sufixos possíveis. Em seguida, você pode combinar o fim do prefixo e o novo sufixo para formar o próximo prefixo e repetir.
Por exemplo, se você começar com o prefixo “Half a”, então a próxima palavra tem que ser “bee”, porque o prefixo só aparece uma vez no texto. O prefixo seguinte é “a bee”, então o próximo sufixo poderia ser “philosophically”, “be” ou “due”.
Neste exemplo, o comprimento do prefixo é sempre dois, mas você pode fazer a análise de Markov com qualquer comprimento de prefixo.
Exercício 13.8
Análise de Markov:
a) Escreva um programa que leia o texto de um arquivo e execute a análise de Markov. O resultado deve ser um dicionário que mapeie prefixos a uma coleção de possíveis sufixos. A coleção pode ser uma lista, tupla ou dicionário; você é que deverá fazer a escolha adequada. Você pode testar seu programa com um comprimento de prefixo 2, mas deve escrever o programa de forma que seja fácil testar outros comprimentos.
b) Acrescente uma função ao programa anterior para gerar texto aleatório baseado na análise de Markov. Aqui está um exemplo de exemplo de Emma com o comprimento de prefixo 2.
He was very clever, be it sweetness or be angry, ashamed or only amused, at such a stroke. She had never thought of Hannah till you were never meant for me?” “I cannot make speeches, Emma:” he soon cut it all himself.
Para este exemplo, deixei a pontuação anexada às palavras. O resultado é quase sintaticamente correto, mas não exatamente. Semanticamente, quase faz sentido, mas não exatamente.
O que acontece se você aumentar o comprimento dos prefixos? O texto aleatório faz mais sentido?
c) Uma vez que o seu programa esteja funcionando, você pode querer tentar uma mistura: se combinar o texto de dois ou mais livros, o texto aleatório gerado misturará o vocabulário e frases das fontes de formas interessantes.
Crédito: este estudo de caso é baseado em um exemplo de Kernighan and Pike, The Practice of Programming, Addison-Wesley, 1999.
É uma boa ideia tentar fazer este exercício antes de continuar; depois você pode baixar a minha solução em http://thinkpython2.com/code/markov.py. Também vai precisar de http://thinkpython2.com/code/emma.txt.
13.9 - Estruturas de dados
Usar análise de Markov para gerar o texto aleatório é divertido, mas também há uma razão para este exercício: a seleção da estrutura de dados. Na sua solução para os exercícios anteriores, você teve que selecionar:
-
como representar os prefixos;
-
como representar a coleção de sufixos possíveis;
-
como representar o mapeamento de cada prefixo à coleção de possíveis sufixos.
O último é fácil: um dicionário é a escolha óbvia para um mapeamento de chaves a valores correspondentes.
Para os prefixos, as opções mais óbvias são strings, listas de strings ou tuplas de strings.
Para os sufixos, uma opção é uma lista; outra é um histograma (dicionário).
Como você deve escolher? O primeiro passo é pensar nas operações que você vai precisar implementar para cada estrutura de dados. Para os prefixos, é preciso poder retirar palavras do começo e acrescentar no fim. Por exemplo, se o prefixo atual é “Half a” e a próxima palavra é “bee”, você tem que poder formar o próximo prefixo, “a bee”.
Sua primeira escolha pode ser uma lista, pois é fácil acrescentar e retirar elementos, mas também precisamos poder usar os prefixos como chaves em um dicionário, para excluir listas. Com tuplas, você não pode acrescentar ou retirar, mas pode usar o operador de adição para formar uma nova tupla:
def shift(prefix, word):
return prefix[1:] + (word)
shift recebe uma tupla de palavras, prefix, e uma string, word, e forma uma nova tupla que tem todas as palavras em prefix, exceto a primeira e word adicionada no final.
Para a coleção de sufixos, as operações que precisamos executar incluem a soma de um novo sufixo (ou aumento da frequência de um existente), e a escolha de um sufixo aleatório.
Acrescentar um novo sufixo é igualmente fácil para a implementação da lista ou do histograma. Escolher um elemento aleatório de uma lista é fácil; escolher de um histograma é mais difícil de fazer de forma eficiente (ver o Exercício 13.7).
Por enquanto, falamos principalmente sobre a facilidade de implementação, mas há outros fatores a considerar na escolha das estruturas de dados. Um deles é o tempo de execução. Às vezes, há uma razão teórica para esperar que uma estrutura de dados seja mais rápida que outra; por exemplo, eu mencionei que o operador in é mais rápido para dicionários que para listas, pelo menos quando o número de elementos é grande.
Porém, muitas vezes não se sabe de antemão qual implementação será mais rápida. Uma opção é implementar ambas e ver qual é melhor. Esta abordagem é chamada de benchmarking. Uma alternativa prática é escolher a estrutura de dados mais fácil para implementar, e então ver se é rápida o suficiente para a aplicação desejada. Se for o caso, não é preciso continuar. Do contrário, há ferramentas, como o módulo profile, que podem identificar os lugares em um programa que tomam mais tempo de execução.
Outro fator a considerar é o espaço de armazenamento. Por exemplo, usar um histograma para a coleção de sufixos pode tomar menos espaço porque só é preciso armazenar cada palavra uma vez, não importa quantas vezes apareça no texto. Em alguns casos, a economia de espaço também pode fazer o seu programa rodar mais rápido e, em casos extremos, seu programa pode simplesmente nem rodar se ficar sem memória. Porém, para muitas aplicações, o espaço é uma consideração secundária depois do tempo de execução.
Um último comentário: nessa discussão, a ideia implícita é que devemos usar uma estrutura de dados tanto para análise como para geração. Entretanto, como essas fases são separadas, também seria possível usar uma estrutura para a análise e então convertê-la em outra estrutura para a geração. Isso seria uma vantagem se o tempo poupado durante a geração excedesse o tempo decorrido na conversão.
13.10 - Depuração
Quando estiver depurando um programa, especialmente se estiver trabalhando em um erro difícil, há cinco coisas que você pode tentar:
Leitura
Examine seu código, leia-o para você mesmo e verifique se diz o que você pensou em dizer.
Execução
Experimente fazer alterações e executar versões diferentes. Muitas vezes, ao se expor a coisa certa no lugar certo do programa, o problema fica óbvio, mas pode ser necessário construir o scaffolding.
Ruminação
Pense por algum tempo! Qual é o tipo do erro: de sintaxe, de tempo de execução ou semântico? Quais informações você consegue obter a partir das mensagens de erro, ou da saída do programa? Que tipo de erro pode causar o problema que está vendo? O que você mudou por último, antes que o problema aparecesse?
Conversa com o pato de borracha (rubberducking)
Ao explicar o problema a alguém, às vezes você consegue encontrar a resposta antes de terminar a explicação. Muitas vezes, não é preciso nem haver outra pessoa; você pode falar até com um pato de borracha. E essa é a origem de uma estratégia bem conhecida chamada de depuração do pato de borracha. Não estou inventando isso, veja https://en.wikipedia.org/wiki/Rubber_duck_debugging.
Retirada
Em um determinado ponto, a melhor coisa a fazer é voltar atrás e desfazer as alterações recentes, até chegar de volta a um programa que funcione e que você entenda. Então você pode começar a reconstruir.
Programadores iniciantes às vezes ficam presos em uma dessas atividades e esquecem das outras. Cada atividade vem com o seu próprio modo de falha.
Por exemplo, a leitura do seu código pode ajudar se o problema é um erro tipográfico, mas não se o problema for conceitual. Se você não entende o que o seu programa faz, pode lê-lo cem vezes e nunca verá o erro, porque o erro está na sua cabeça.
Fazer experiências pode ajudar, especialmente se você executar testes pequenos e simples. No entanto, se executar experiências sem pensar ou ler seu código, pode cair em um padrão que chamo de “programação aleatória”, que é o processo de fazer alterações aleatórias até que o programa faça a coisa certa. Obviamente, a programação aleatória pode levar muito tempo.
É preciso pensar um pouco. A depuração é como ciência experimental. Deve haver pelo menos uma hipótese sobre qual é o problema. Se houver duas ou mais possibilidades, tente pensar em um teste que eliminaria uma delas.
Não obstante, até as melhores técnicas de depuração falharão se houver erros demais, ou se o código que está tentando corrigir for grande e complicado demais. Às vezes, a melhor opção é voltar atrás, simplificando o programa até chegar a algo que funcione e que você entenda.
Programadores iniciantes muitas vezes relutam em voltar atrás porque não suportam a ideia de eliminar sequer uma linha de código (mesmo se estiver errada). Para você se sentir melhor, copie seu programa em outro arquivo antes de começar a desmontá-lo. Então você pode copiar as partes de volta, uma a uma.
Encontrar um erro difícil exige leitura, execução, ruminação, e, às vezes, a retirada. Se empacar em alguma dessas atividades, tente as outras.
13.11 - Glossário
determinista
Relativo a um programa que faz a mesma coisa cada vez que é executado, se receber as mesmas entradas.
pseudoaleatório
Relativo a uma sequência de números que parecem ser aleatórios, mas que são gerados por um programa determinista.
valor padrão
Valor dado a um parâmetro opcional se não houver nenhum argumento.
ignorar (override)
Substituir um valor padrão por um argumento.
benchmarking
Processo de escolha entre estruturas de dados pela implementação de alternativas e testes em uma amostra de entradas possíveis.
depuração do pato de borracha
Depurar explicando o problema a um objeto inanimado como um pato de borracha. Articular o problema pode ajudar a resolvê-lo, mesmo se o pato de borracha não conhecer Python.
13.12 - Exercícios
Exercício 13.9
A “classificação” de uma palavra é a sua posição em uma lista de palavras classificadas por frequência: a palavra mais comum tem a classificação 1, a segunda mais comum é 2 etc.
A lei de Zipf descreve a relação entre classificações e frequências das palavras em linguagens naturais (http://en.wikipedia.org/wiki/Zipf's_law). Ela prevê especificamente que a frequência, f, da palavra com classificação r é:
f = cr−s
onde s e c são parâmetros que dependem do idioma e do texto. Se você tomar o logaritmo de ambos os lados desta equação, obtém:
log f = log c − s log r
Se você traçar o log de f contra o log de r, terá uma linha reta com uma elevação -s e interceptar o log de c.
Escreva um programa que leia um texto em um arquivo, conte as frequências das palavras e exiba uma linha para cada palavra, em ordem descendente da frequência, com log de f e log de r. Use o programa gráfico de sua escolha para traçar os resultados e verifique se formam uma linha reta. Você pode estimar o valor de s?
Solução: http://thinkpython2.com/code/zipf.py. Para executar a minha solução, você vai precisar do módulo de gráficos matplotlib. Se você instalou o Anaconda, já tem o matplotlib; se não tiver, é preciso instalá-lo.
Capítulo 14: Arquivos
Este capítulo apresenta a ideia de programas “persistentes”, que mantêm dados em armazenamento permanente, e mostra como usar tipos diferentes de armazenamento permanente, como arquivos e bancos de dados.
14.1 - Persistência
A maioria dos programas que vimos até agora são transitórios, porque são executados por algum tempo e produzem alguma saída, mas, quando terminam, seus dados desaparecem. Se executar o programa novamente, ele começa novamente do zero.
Outros programas são persistentes: rodam por muito tempo (ou todo o tempo); mantêm pelo menos alguns dos seus dados em armazenamento permanente (uma unidade de disco rígido, por exemplo); e se são desligados e reiniciados, continuam de onde pararam.
Exemplos de programas persistentes são sistemas operacionais, que rodam praticamente durante todo o tempo em que um computador está ligado, e servidores web, que rodam todo o tempo, esperando pedidos de entrada na rede.
Uma das formas mais simples para programas manterem seus dados é lendo e escrevendo arquivos de texto. Já vimos programas que leem arquivos de texto; neste capítulo veremos programas que os escrevem.
Uma alternativa é armazenar o estado do programa em um banco de dados. Neste capítulo apresentarei um banco de dados simples e um módulo, pickle, que facilita o armazenamento de dados de programas.
14.2 - Leitura e escrita
Um arquivo de texto é uma sequência de caracteres armazenados em um meio permanente como uma unidade de disco rígido, pendrive ou CD-ROM. Vimos como abrir e ler um arquivo em “Leitura de listas de palavras” na página 133.
Para escrever um arquivo texto, é preciso abri-lo com o modo 'w' como segundo parâmetro:
>>> fout = open('output.txt', 'w')
Se o arquivo já existe, abri-lo em modo de escrita elimina os dados antigos e começa tudo de novo, então tenha cuidado! Se o arquivo não existir, é criado um arquivo novo.
open retorna um objeto de arquivo que fornece métodos para trabalhar com o arquivo. O método write põe dados no arquivo:
>>> line1 = "This here's the wattle,\n"
>>> fout.write(line1)
24
O valor devolvido é o número de caracteres que foram escritos. O objeto de arquivo monitora a posição em que está, então se você chamar write novamente, os novos dados são acrescentados ao fim do arquivo:
>>> line2 = "the emblem of our land.\n"
>>> fout.write(line2)
24
Ao terminar de escrever, você deve fechar o arquivo:
>>> fout.close()
Se não fechar o arquivo, ele é fechado para você quando o programa termina.
14.3 - Operador de formatação
O argumento de write tem que ser uma string, então, se quisermos inserir outros valores em um arquivo, precisamos convertê-los em strings. O modo mais fácil de fazer isso é com str:
>>> x = 52
>>> fout.write(str(x))
Uma alternativa é usar o operador de formatação, %. Quando aplicado a números inteiros, % é o operador de módulo. No entanto, quando o primeiro operando é uma string, % é o operador de formatação.
O primeiro operando é a string de formatação, que contém uma ou várias sequências de formatação que especificam como o segundo operando deve ser formatado. O resultado é uma string.
Por exemplo, a sequência de formatação '%d' significa que o segundo operando deve ser formatado como um número inteiro decimal:
>>> camels = 42
>>> '%d' % camels
'42'
O resultado é a string '42', que não deve ser confundida com o valor inteiro 42.
Uma sequência de formatação pode aparecer em qualquer lugar na string, então você pode embutir um valor em uma sentença:
>>> 'I have spotted %d camels.' % camels
'I have spotted 42 camels.'
Se houver mais de uma sequência de formatação na string, o segundo argumento tem que ser uma tupla. Cada sequência de formatação é combinada com um elemento da tupla, nesta ordem.
O seguinte exemplo usa '%d' para formatar um número inteiro, '%g' para formatar um número de ponto flutuante e '%s' para formatar qualquer objeto como uma string:
>>> 'In %d years I have spotted %g %s.' % (3, 0.1, 'camels')
'In 3 years I have spotted 0.1 camels.'
O número de elementos na tupla tem de corresponder ao número de sequências de formatação na string. Além disso, os tipos dos elementos têm de corresponder às sequências de formatação:
>>> '%d %d %d' % (1, 2)
TypeError: not enough arguments for format string
>>> '%d' % 'dollars'
TypeError: %d format: a number is required, not str
No primeiro exemplo não há elementos suficientes; no segundo, o elemento é do tipo incorreto.
Para obter mais informações sobre o operador de formato, veja https://docs.python.org/3/library/stdtypes.html#printf-style-string-formatting. Você pode ler sobre uma alternativa mais eficiente, o método de formatação de strings, em https://docs.python.org/3/library/stdtypes.html#str.format.
14.4 - Nomes de arquivo e caminhos
Os arquivos são organizados em diretórios (também chamados de “pastas”). Cada programa em execução tem um “diretório atual”, que é o diretório-padrão da maior parte das operações. Por exemplo, quando você abre um arquivo de leitura, Python o procura no diretório atual.
O módulo os fornece funções para trabalhar com arquivos e diretórios (“os” é a abreviação de “sistema operacional” em inglês). os.getcwd devolve o nome do diretório atual:
>>> import os
>>> cwd = os.getcwd()
>>> cwd
'/home/dinsdale'
cwd é a abreviação de “diretório de trabalho atual” em inglês. O resultado neste exemplo é /home/dinsdale, que é o diretório-padrão de um usuário chamado “dinsdale”.
Uma string como '/home/dinsdale', que identifica um arquivo ou diretório, é chamada de caminho (path).
Um nome de arquivo simples, como memo.txt, também é considerado um caminho, mas é um caminho relativo, porque se relaciona ao diretório atual. Se o diretório atual é /home/dinsdale, o nome de arquivo memo.txt se referiria a /home/dinsdale/memo.txt.
Um caminho que começa com / não depende do diretório atual; isso é chamado de caminho absoluto. Para encontrar o caminho absoluto para um arquivo, você pode usar os.path.abspath:
>>> os.path.abspath('memo.txt')
'/home/dinsdale/memo.txt'
os.path fornece outras funções para trabalhar com nomes de arquivo e caminhos. Por exemplo, os.path.exists que verifica se um arquivo ou diretório existe:
>>> os.path.exists('memo.txt')
True
Se existir, os.path.isdir verifica se é um diretório:
>>> os.path.isdir('memo.txt')
False
>>> os.path.isdir('/home/dinsdale')
True
De forma similar, os.path.isfile verifica se é um arquivo.
os.listdir retorna uma lista dos arquivos (e outros diretórios) no diretório dado:
>>> os.listdir(cwd)
['music', 'photos', 'memo.txt']
Para demonstrar essas funções, o exemplo seguinte “passeia” por um diretório, exibe os nomes de todos os arquivos e chama a si mesmo recursivamente em todos os diretórios:
def walk(dirname):
for name in os.listdir(dirname):
path = os.path.join(dirname, name)
if os.path.isfile(path):
print(path)
else:
walk(path)
os.path.join recebe um diretório e um nome de arquivo e os une em um caminho completo.
O módulo os fornece uma função chamada walk, que é semelhante, só que mais versátil. Como exercício, leia a documentação e use-a para exibir os nomes dos arquivos em um diretório dado e seus subdiretórios. Você pode baixar minha solução em http://thinkpython2.com/code/walk.py.
14.5 - Captura de exceções
Muitas coisas podem dar errado quando você tenta ler e escrever arquivos. Se tentar abrir um arquivo que não existe, você recebe um IOError:
>>> fin = open('bad_file')
IOError: [Errno 2] No such file or directory: 'bad\_file'
Se não tiver permissão para acessar um arquivo:
>>> fout = open('/etc/passwd', 'w')
PermissionError: [Errno 13] Permission denied: '/etc/passwd'
E se tentar abrir um diretório para leitura, recebe
>>> fin = open('/home')
IsADirectoryError: [Errno 21] Is a directory: '/home'
Para evitar esses erros, você pode usar funções como os.path.exists e os.path.isfile, mas levaria muito tempo e código para verificar todas as possibilidades (se "Errno 21" significa algo, pode ser que pelo menos 21 coisas podem dar errado).
É melhor ir em frente e tentar, e lidar com problemas se eles surgirem, que é exatamente o que a instrução try faz. A sintaxe é semelhante à da instrução if…else:
try:
fin = open('bad_file')
except:
print('Something went wrong.')
O Python começa executando a cláusula try. Se tudo for bem, ele ignora a cláusula except e prossegue. Se ocorrer uma exceção, o programa sai da cláusula try e executa a cláusula except.
Lidar com exceções usando uma instrução try chama-se capturar uma exceção. Neste exemplo, a cláusula except exibe uma mensagem de erro que não é muito útil. Em geral, a captura de uma exceção oferece a oportunidade de corrigir o problema ou tentar novamente, ou, ao menos, de terminar o programa adequadamente.
14.6 - Bancos de dados
Um banco de dados é um arquivo organizado para armazenar dados. Muitos bancos de dados são organizados como um dicionário, porque mapeiam chaves a valores. A maior diferença entre um banco de dados e um dicionário é que o banco de dados está em um disco (ou outro armazenamento permanente), portanto persiste depois que o programa termina.
O módulo dbm fornece uma interface para criar e atualizar arquivos de banco de dados. Como exemplo, criarei um banco de dados que contém legendas de arquivos de imagem.
Abrir um banco de dados é semelhante à abertura de outros arquivos:
>>> import dbm
>>> db = dbm.open('captions', 'c')
O modo 'c' significa que o banco de dados deve ser criado, se ainda não existir. O resultado é um objeto de banco de dados que pode ser usado (para a maior parte das operações) como um dicionário.
Quando você cria um novo item, dbm atualiza o arquivo de banco de dados:
>>> db['cleese.png'] = 'Photo of John Cleese.'
Quando você acessa um dos itens, dbm lê o arquivo:
>>> db['cleese.png']
b'Photo of John Cleese.'
O resultado é um objeto bytes, o que explica o prefixo b. Um objeto bytes é semelhante a uma string, em muitos aspectos. Quando você avançar no Python, a diferença se tornará importante, mas, por enquanto, podemos ignorá-la.
Se fizer outra atribuição a uma chave existente, o dbm substitui o valor antigo:
>>> db['cleese.png'] = 'Photo of John Cleese doing a silly walk.'
>>> db['cleese.png']
b'Photo of John Cleese doing a silly walk.'
Alguns métodos de dicionário, como keys e items, não funcionam com objetos de banco de dados. No entanto, a iteração com um loop for, sim:
for key in db:
print(key, db[key])
Como em outros arquivos, você deve fechar o banco de dados quando terminar:
>>> db.close()
14.7 - Usando o Pickle
Uma limitação de dbm é que as chaves e os valores têm que ser strings ou bytes. Se tentar usar algum outro tipo, vai receber um erro.
O módulo pickle pode ajudar. Ele traduz quase qualquer tipo de objeto em uma string conveniente para o armazenamento em um banco de dados, e então traduz strings de volta em objetos.
pickle.dumps recebe um objeto como parâmetro e retorna uma representação de string:
>>> import pickle
>>> t = [1, 2, 3]
>>> pickle.dumps(t)
b'\x80\x03]q\x00(K\x01K\x02K\x03e.'
O formato não é óbvio para leitores humanos; o objetivo é que seja fácil para o pickle interpretar. pickle.loads reconstitui o objeto:
>>> t1 = [1, 2, 3]
>>> s = pickle.dumps(t1)
>>> t2 = pickle.loads(s)
>>> t2
[1, 2, 3]
Embora o novo objeto tenha o mesmo valor que o antigo, não é (em geral) o mesmo objeto:
>>> t1 == t2
True
>>> t1 is t2
False
Em outras palavras, usar o pickle.dumps e pickle.loads tem o mesmo efeito que copiar o objeto.
Você pode usar o pickle para guardar variáveis que não são strings em um banco de dados. Na verdade, esta combinação é tão comum que foi encapsulada em um módulo chamado shelve.
14.8 - Pipes
A maior parte dos sistemas operacionais fornece uma interface de linha de comando, conhecida como shell. Shells normalmente fornecem comandos para navegar nos sistemas de arquivos e executar programas. Por exemplo, em Unix você pode alterar diretórios com cd, exibir o conteúdo de um diretório com ls e abrir um navegador web digitando (por exemplo) firefox.
Qualquer programa que possa ser aberto no shell também pode ser aberto no Python usando um objeto pipe, que representa um programa em execução.
Por exemplo, o comando Unix ls -l normalmente exibe o conteúdo do diretório atual no formato longo. Você pode abrir ls com os.popen[1]:
>>> cmd = 'ls -l'
>>> fp = os.popen(cmd)
O argumento é uma string que contém um comando shell. O valor de retorno é um objeto que se comporta como um arquivo aberto. É possível ler a saída do processo ls uma linha por vez com readline ou receber tudo de uma vez com read:
>>> res = fp.read()
Ao terminar, feche o pipe como se fosse um arquivo:
>>> stat = fp.close()
>>> print(stat)
None
O valor de retorno é o status final do processo ls; None significa que terminou normalmente (sem erros).
Por exemplo, a maior parte dos sistemas Unix oferece um comando chamado md5sum, que lê o conteúdo de um arquivo e calcula uma assinatura digital. Você pode ler sobre o MD5 em http://en.wikipedia.org/wiki/Md5. Este comando fornece uma forma eficiente de verificar se dois arquivos têm o mesmo conteúdo. A probabilidade de dois conteúdos diferentes produzirem a mesma assinatura digital é muito pequena (isto é, muito pouco provável que aconteça antes do colapso do universo).
Você pode usar um pipe para executar o md5sum do Python e receber o resultado:
>>> filename = 'book.tex'
>>> cmd = 'md5sum ' + filename
>>> fp = os.popen(cmd)
>>> res = fp.read()
>>> stat = fp.close()
>>> print(res)
1e0033f0ed0656636de0d75144ba32e0 book.tex
>>> print(stat)
None
14.9 - Escrevendo módulos
Qualquer arquivo que contenha código do Python pode ser importado como um módulo. Por exemplo, vamos supor que você tenha um arquivo chamado wc.py com o seguinte código:
def linecount(filename):
count = 0
for line in open(filename):
count += 1
return count
print(linecount('wc.py'))
Quando este programa é executado, ele lê a si mesmo e exibe o número de linhas no arquivo, que é 7. Você também pode importá-lo desta forma:
>>> import wc
7
Agora você tem um objeto de módulo wc:
>>> wc
<module 'wc' from 'wc.py'>
O objeto de módulo fornece o linecount:
>>> wc.linecount('wc.py')
7
Então é assim que se escreve módulos no Python.
O único problema com este exemplo é que quando você importa o módulo, ele executa o código de teste no final. Normalmente, quando se importa um módulo, ele define novas funções, mas não as executa.
Os programas que serão importados como módulos muitas vezes usam a seguinte expressão:
if __name__ == '__main__':
print(linecount('wc.py'))
__name__ é uma variável integrada, estabelecida quando o programa inicia. Se o programa estiver rodando como um script, __name__ tem o valor '__main__'; neste caso, o código de teste é executado. Do contrário, se o módulo está sendo importado, o código de teste é ignorado.
Como exercício, digite este exemplo em um arquivo chamado wc.py e execute-o como um script. Então execute o interpretador do Python e import wc. Qual é o valor de __name__ quando o módulo está sendo importado?
Atenção: se você importar um módulo que já tenha sido importado, o Python não faz nada. Ele não relê o arquivo, mesmo se tiver sido alterado.
Se quiser recarregar um módulo, você pode usar a função integrada reload, mas isso pode causar problemas, então o mais seguro é reiniciar o interpretador e importar o módulo novamente.
14.10 - Depuração
Quando estiver lendo e escrevendo arquivos, você pode ter problemas com whitespace. Esses erros podem ser difíceis para depurar, porque os espaços, tabulações e quebras de linha normalmente são invisíveis:
>>> s = '1 2\t 3\n 4'
>>> print(s)
1 2 3
4
A função integrada repr pode ajudar. Ela recebe qualquer objeto como argumento e retorna uma representação em string do objeto. Para strings, representa caracteres de whitespace com sequências de barras invertidas:
>>> print(repr(s))
'1 2\t 3\n 4'
Isso pode ser útil para a depuração.
Outro problema que você pode ter é que sistemas diferentes usam caracteres diferentes para indicar o fim de uma linha. Alguns sistemas usam newline, representado por \n. Outros usam um caractere de retorno, representado por \r. Alguns usam ambos. Se mover arquivos entre sistemas diferentes, essas inconsistências podem causar problemas.
Para a maior parte dos sistemas há aplicações para converter de um formato a outro. Você pode encontrá-los (e ler mais sobre o assunto) em http://en.wikipedia.org/wiki/Newline. Ou, é claro, você pode escrever um por conta própria.
14.11 - Glossário
persistente
Relativo a um programa que roda indefinidamente e mantém pelo menos alguns dos seus dados em armazenamento permanente.
operador de formatação
Um operador, %, que recebe uma string de formatação e uma tupla e gera uma string que inclui os elementos da tupla formatada como especificado pela string de formatação.
string de formatação
String usada com o operador de formatação, que contém sequências de formatação.
sequência de formatação
Sequência de caracteres em uma string de formatação, como %d, que especifica como um valor deve ser formatado.
arquivo de texto
Sequência de caracteres guardados em armazenamento permanente, como uma unidade de disco rígido.
diretório
Uma coleção de arquivos nomeada, também chamada de pasta.
caminho
String que identifica um arquivo.
caminho relativo
Caminho que inicia no diretório atual.
caminho absoluto
Caminho que inicia no diretório de posição mais alta (raiz) no sistema de arquivos.
capturar
Impedir uma exceção de encerrar um programa usando as instruções try e except.
banco de dados
Um arquivo cujo conteúdo é organizado como um dicionário, com chaves que correspondem a valores.
objeto bytes
Objeto semelhante a uma string.
shell
Programa que permite aos usuários digitar comandos e executá-los para iniciar outros programas.
objeto pipe
Objeto que representa um programa em execução, permitindo que um programa do Python execute comandos e leia os resultados.
14.12 - Exercícios
Exercício 14.1
Escreva uma função chamada sed que receba como argumentos uma string-padrão, uma string de substituição e dois nomes de arquivo; ela deve ler o primeiro arquivo e escrever o conteúdo no segundo arquivo (criando-o, se necessário). Se a string-padrão aparecer em algum lugar do arquivo, ela deve ser substituída pela string de substituição.
Se ocorrer um erro durante a abertura, leitura, escrita ou fechamento dos arquivos, seu programa deve capturar a exceção, exibir uma mensagem de erro e encerrar.
Solução: http://thinkpython2.com/code/sed.py.
Exercício 14.2
Se você baixar minha solução do Exercício 12.2 em http://thinkpython2.com/code/anagram_sets.py, verá que ela cria um dicionário que mapeia uma string ordenada de letras à lista de palavras que podem ser soletradas com aquelas letras. Por exemplo, 'opst' mapeia à lista ['opts', 'post', 'pots', 'spot', 'stop', 'tops'].
Escreva um módulo que importe anagram_sets e forneça duas novas funções: store_anagrams deve guardar o dicionário de anagramas em uma “prateleira” (objeto criado pelo módulo sheve); read_anagrams deve procurar uma palavra e devolver uma lista dos seus anagramas.
Solução: http://thinkpython2.com/code/anagram_db.py.
Exercício 14.3
Em uma grande coleção de arquivos MP3 pode haver mais de uma cópia da mesma música, guardada em diretórios diferentes ou com nomes de arquivo diferentes. A meta deste exercício é procurar duplicatas.
-
Escreva um programa que procure um diretório e todos os seus subdiretórios, recursivamente, e retorne uma lista de caminhos completos de todos os arquivos com um dado sufixo (como .mp3). Dica: os.path fornece várias funções úteis para manipular nomes de caminhos e de arquivos.
-
Para reconhecer duplicatas, você pode usar md5sum para calcular uma “soma de controle” para cada arquivo. Se dois arquivos tiverem a mesma soma de controle, provavelmente têm o mesmo conteúdo.
-
Para conferir o resultado, você pode usar o comando Unix
diff.
Solução: http://thinkpython2.com/code/find_duplicates.py.
Capítulo 15: Classes e objetos
A esta altura você já sabe como usar funções para organizar código e tipos integrados para organizar dados. O próximo passo é aprender “programação orientada a objeto”, que usa tipos definidos pelos programadores para organizar tanto o código quanto os dados. A programação orientada a objeto é um tópico abrangente; será preciso passar por alguns capítulos para abordar o tema.
Os exemplos de código deste capítulo estão disponíveis em http://thinkpython2.com/code/Point1.py; as soluções para os exercícios estão disponíveis em http://thinkpython2.com/code/Point1_soln.py.
15.1 - Tipos definidos pelos programadores
Já usamos muitos tipos integrados do Python; agora vamos definir um tipo próprio. Como exemplo, criaremos um tipo chamado Point, que representa um ponto no espaço bidimensional.
Na notação matemática, os pontos muitas vezes são escritos entre parênteses, com uma vírgula separando as coordenadas. Por exemplo, (0,0) representa a origem e (x, y) representa o ponto que está x unidades à direita e y unidades acima da origem.
Há várias formas para representar pontos no Python:
-
Podemos armazenar as coordenadas separadamente em duas variáveis, x e y.
-
Podemos armazenar as coordenadas como elementos em uma lista ou tupla.
-
Podemos criar um tipo para representar pontos como objetos.
Criar um tipo é mais complicado que outras opções, mas tem vantagens que logo ficarão evidentes.
Um tipo definido pelo programador também é chamado de classe. Uma definição de classe pode ser assim:
class Point:
"""Represents a point in 2-D space."""
O cabeçalho indica que a nova classe se chama Point. O corpo é uma docstring que explica para que a classe serve. Você pode definir variáveis e métodos dentro de uma definição de classe, mas voltaremos a isso depois.
Definir uma classe denominada Point cria um objeto de classe:
>>> Point
<class '__main__.Point'>
Como Point é definido no nível superior, seu “nome completo” é __main__.Point.
O objeto de classe é como uma fábrica para criar objetos. Para criar um Point, você chama Point como se fosse uma função:
>>> blank = Point()
>>> blank
<__main__.Point object at 0xb7e9d3ac>
O valor de retorno é uma referência a um objeto Point, ao qual atribuímos blank.
Criar um objeto chama-se instanciação, e o objeto é uma instância da classe.
Quando você exibe uma instância, o Python diz a que classe ela pertence e onde está armazenada na memória (o prefixo o 0x significa que o número seguinte está em formato hexadecimal).
Cada objeto é uma instância de alguma classe, então “objeto” e “instância” são intercambiáveis. Porém, neste capítulo uso “instância” para indicar que estou falando sobre um tipo definido pelo programador.
15.2 - Atributos
Você pode atribuir valores a uma instância usando a notação de ponto:
>>> blank.x = 3.0
>>> blank.y = 4.0
Essa sintaxe é semelhante à usada para selecionar uma variável de um módulo, como math.pi ou string.whitespace. Nesse caso, entretanto, estamos atribuindo valores a elementos nomeados de um objeto. Esses elementos chamam-se atributos.
Em inglês, quando é um substantivo, a palavra “AT-trib-ute” é pronunciada com ênfase na primeira sílaba, ao contrário de “a-TRIB-ute”, que é um verbo.
O diagrama seguinte mostra o resultado dessas atribuições. Um diagrama de estado que mostra um objeto e seus atributos chama-se diagrama de objeto; veja a Figura 15.1.
 .
.
Figura 15.1 – Diagrama de um objeto Point.
A variável blank refere-se a um objeto Point, que contém dois atributos. Cada atributo refere-se a um número de ponto flutuante.
Você pode ler o valor de um atributo usando a mesma sintaxe:
>>> blank.y
4.0
>>> x = blank.x
>>> x
3.0
A expressão blank.x significa “Vá ao objeto a que blank se refere e pegue o valor de x”. No exemplo, atribuímos este valor a uma variável x. Não há nenhum conflito entre a variável x e o atributo x.
Você pode usar a notação de ponto como parte de qualquer expressão. Por exemplo:
>>> '(%g, %g)' % (blank.x, blank.y)
'(3.0, 4.0)'
>>> distance = math.sqrt(blank.x ** 2 + blank.y ** 2)
>>> distance
5.0
Você pode passar uma instância como argumento da forma habitual. Por exemplo:
def print_point(p):
print('(%g, %g)' % (p.x, p.y))
print_point toma um ponto como argumento e o exibe em notação matemática. Para invocá-lo, você pode passar blank como argumento:
>>> print_point(blank)
(3.0, 4.0)
Dentro da função, p é um alias para blank, então, se a função altera p, blank também muda.
Como exercício, escreva uma função chamada distance_between_points, que toma dois pontos como argumentos e retorna a distância entre eles.
15.3 - Retângulos
Às vezes, é óbvio quais deveriam ser os atributos de um objeto, mas outras é preciso decidir entre as possibilidades. Por exemplo, vamos supor que você esteja criando uma classe para representar retângulos. Que atributos usaria para especificar a posição e o tamanho de um retângulo? Você pode ignorar ângulo; para manter as coisas simples, suponha que o retângulo seja vertical ou horizontal.
Há duas possibilidades, no mínimo:
-
Você pode especificar um canto do retângulo (ou o centro), a largura e a altura.
-
Você pode especificar dois cantos opostos.
Nesse ponto é difícil dizer qual opção é melhor, então implementaremos a primeira, como exemplo.
Aqui está a definição de classe:
class Rectangle:
"""Represents a rectangle.
attributes: width, height, corner.
"""
A docstring lista os atributos: width e height são números; corner é um objeto Point que especifica o canto inferior esquerdo.
Para representar um retângulo, você tem que instanciar um objeto Rectangle e atribuir valores aos atributos:
box = Rectangle()
box.width = 100.0
box.height = 200.0
box.corner = Point()
box.corner.x = 0.0
box.corner.y = 0.0
A expressão box.corner.x significa “Vá ao objeto ao qual box se refere e pegue o atributo denominado corner; então vá a este objeto e pegue o atributo denominado x”.
A Figura 15.2 mostra o estado deste objeto. Um objeto que é um atributo de outro objeto é integrado.
A Figura 10.1 mostra o diagrama de estado para cheeses, numbers e empty.
 .
.
Figura 15.2 – Diagrama de um objeto Rectangle.
15.4 - Instâncias como valores de retorno
As funções podem retornar instâncias. Por exemplo, find_center recebe um Rectangle como argumento e devolve um Point, que contém as coordenadas do centro do retângulo:
def find_center(rect):
p = Point()
p.x = rect.corner.x + rect.width/2
p.y = rect.corner.y + rect.height/2
return p
Aqui está um exemplo que passa box como um argumento para find_center e atribui o ponto resultante à variável center:
>>> center = find_center(box)
>>> print_point(center)
(50, 100)
15.5 - Objetos são mutáveis
Você pode alterar o estado de um objeto fazendo uma atribuição a um dos seus atributos. Por exemplo, para mudar o tamanho de um retângulo sem mudar sua posição, você pode alterar os valores de width e height:
box.width = box.width + 50
box.height = box.height + 100
Você também pode escrever funções que alteram objetos. Por exemplo, grow_rectangle recebe um objeto Rectangle e dois números, dwidth e dheight, e adiciona os números à largura e altura do retângulo:
def grow_rectangle(rect, dwidth, dheight):
rect.width += dwidth
rect.height += dheight
Eis um exemplo que demonstra o efeito:
>>> box.width, box.height
(150.0, 300.0)
>>> grow_rectangle(box, 50, 100)
>>> box.width, box.height
(200.0, 400.0)
Dentro da função, rect é um alias de box, então quando a função altera rect, box aponta para o objeto alterado.
Como exercício, escreva uma função chamada move_rectangle que toma um Rectangle e dois números chamados dx e dy. Ela deve alterar a posição do retângulo, adicionando dx à coordenada x de corner e adicionando dy à coordenada y de corner.
15.6 - Cópia
Alias podem tornar um programa difícil de ler porque as alterações em um lugar podem ter efeitos inesperados em outro lugar. É difícil monitorar todas as variáveis que podem referir-se a um dado objeto.
Em vez de usar alias, copiar o objeto pode ser uma alternativa. O módulo copy contém uma função chamada copy que pode duplicar qualquer objeto:
>>> p1 = Point()
>>> p1.x = 3.0
>>> p1.y = 4.0
>>> import copy
>>> p2 = copy.copy(p1)
p1 e p2 contêm os mesmos dados, mas não são o mesmo Point:
>>> print_point(p1)
(3, 4)
>>> print_point(p2)
(3, 4)
>>> p1 is p2
False
>>> p1 == p2
False
O operador is indica que p1 e p2 não são o mesmo objeto, que é o que esperamos. Porém, você poderia ter esperado que == fosse apresentado como True, porque esses pontos contêm os mesmos dados. Nesse caso, pode ficar desapontado ao saber que, para instâncias, o comportamento padrão do operador == é o mesmo que o do operador is; ele verifica a identidade dos objetos, não a sua equivalência. Isso acontece porque, para tipos definidos pelo programador, o Python não sabe o que deve ser considerado equivalente. Pelo menos, ainda não.
Se você usar copy.copy para duplicar um retângulo, descobrirá que ele copia o objeto Rectangle, mas não o Point embutido nele:
>>> box2 = copy.copy(box)
>>> box2 is box
False
>>> box2.corner is box.corner
True
A Figura 15.3 mostra como fica o diagrama de objeto. Esta operação chama-se cópia superficial porque copia o objeto e qualquer referência que contenha, mas não os objetos integrados.
 .
.
Figura 15.3 – Diagrama: dois objetos Rectangle compartilhando o mesmo Point.
Para a maior parte das aplicações, não é isso que você quer. Nesse exemplo, invocar grow_rectangle em um dos Rectangles não afetaria o outro, mas invocar move_rectangle em qualquer um deles afetaria a ambos! Esse comportamento é confuso e propenso a erros.
Felizmente, o módulo copy oferece um método chamado deepcopy que copia não só o objeto, mas também os objetos aos quais ele se refere, e os objetos aos quais estes se referem, e assim por diante. Você não se surpreenderá ao descobrir que esta operação se chama cópia profunda.
>>> box3 = copy.deepcopy(box)
>>> box3 is box
False
>>> box3.corner is box.corner
False
box3 e box são objetos completamente separados.
Como exercício, escreva uma versão de move_rectangle que cria e retorne um novo retângulo em vez de alterar o antigo.
15.7 - Depuração
Ao começar a trabalhar com objetos, provavelmente você encontrará algumas novas exceções. Se tentar acessar um atributo que não existe, recebe um AttributeError:
>>> p = Point()
>>> p.x = 3
>>> p.y = 4
>>> p.z
AttributeError: Point instance has no attribute 'z'
Se não estiver certo sobre o tipo que um objeto é, pode perguntar:
>>> type(p)
<class '__main__.Point'>
Você também pode usar isinstance para verificar se um objeto é uma instância de uma classe:
>>> isinstance(p, Point)
True
Caso não tenha certeza se um objeto tem determinado atributo, você pode usar a função integrada hasattr:
>>> hasattr(p, 'x')
True
>>> hasattr(p, 'z')
False
O primeiro argumento pode ser qualquer objeto; o segundo argumento é uma string com o nome do atributo.
Você também pode usar uma instrução try para ver se o objeto tem os atributos de que precisa:
try:
x = p.x
except AttributeError:
x = 0
Essa abordagem pode facilitar a escrita de funções que atuam com tipos diferentes; você verá mais informações sobre isso em “Polimorfismo”, na página 248.
15.8 - Glossário
classe
Tipo definido pelo programador. Uma definição de classe cria um objeto de classe.
objeto de classe
Objeto que contém a informação sobre um tipo definido pelo programador. O objeto de classe pode ser usado para criar instâncias do tipo.
instância
Objeto que pertence a uma classe.
instanciar
Criar um objeto.
atributo
Um dos valores denominados associados a um objeto.
objeto integrado
Objeto que é armazenado como um atributo de outro objeto.
cópia superficial
Copiar o conteúdo de um objeto, inclusive qualquer referência a objetos integrados; implementada pela função copy no módulo copy.
cópia profunda
Copiar o conteúdo de um objeto, bem como qualquer objeto integrado, e qualquer objeto integrado a estes, e assim por diante; implementado pela função deepcopy no módulo copy.
diagrama de objeto
Diagrama que mostra objetos, seus atributos e os valores dos atributos.
15.9 - Exercícios
Exercício 15.1
-
Escreva uma definição para uma classe denominada
Circle, com os atributos center e radius, onde center é um objetoPointe radius é um número. -
Instancie um objeto
Circle, que represente um círculo com o centro em 150, 100 e raio 75. -
Escreva uma função denominada
point_in_circle, que tome umCirclee umPointe retorneTrue, se o ponto estiver dentro ou no limite do círculo. -
Escreva uma função chamada
rect_in_circle, que tome umCirclee um Rectangle e retorneTrue, se o retângulo estiver totalmente dentro ou no limite do círculo. -
Escreva uma função denominada
rect_circle_overlap, que tome umCirclee um Rectangle e retorneTrue, se algum dos cantos do retângulo cair dentro do círculo. Ou, em uma versão mais desafiadora, retorneTruese alguma parte do retângulo cair dentro do círculo.
Solução: http://thinkpython2.com/code/Circle.py.
Exercício 15.2
-
Escreva uma função chamada
draw_rectque receba um objetoTurtlee umRectanglee use oTurtlepara desenhar o retângulo. Veja no Capítulo 4 os exemplos de uso de objetosTurtle. -
Escreva uma função chamada
draw_circle, que tome um Turtle e umCirclee desenhe o círculo.
Capítulo 16: Classes e funções
Agora que sabemos como criar tipos, o próximo passo deve ser escrever funções que recebam objetos definidos pelo programador como parâmetros e os retornem como resultados. Neste capítulo também vou apresentar o “estilo funcional de programação” e dois novos planos de desenvolvimento de programas.
Os exemplos de código deste capítulo estão disponíveis em http://thinkpython2.com/code/Time1.py. As soluções para os exercícios estão em http://thinkpython2.com/code/Time1_soln.py.
16.1 - Time
Para ter mais um exemplo de tipo definido pelo programador, criaremos uma classe chamada Time (hora), que registra um horário no dia. A definição da classe é assim:
class Time:
"""Represents the time of day.
attributes: hour, minute, second
"""
Podemos criar um objeto Time e ter atributos para horas, minutos e segundos:
time = Time()
time.hour = 11
time.minute = 59
time.second = 30
O diagrama de estado do objeto Time está na Figura 16.1.
 .
.
Figura 16.1 – Diagrama de um objeto Time.
Como exercício, escreva uma função chamada print_time, que receba um objeto Time e o exiba na forma hour:minute:second. Dica: a sequência de formatação '%.2d' exibe um número inteiro com, pelo menos, dois dígitos, incluindo um zero à esquerda, se for necessário.
Escreva uma função booleana chamada is_after, que receba dois objetos Time, t1 e t2, e devolva True se t1 for cronologicamente depois de t2 e False se não for. Desafio: não use uma instrução if.
16.2 - Funções puras
Nas próximas seções, vamos escrever duas funções que adicionam valores de tempo. Elas demonstram dois tipos de funções: funções puras e modificadores. Também demonstram um plano de desenvolvimento que chamarei de protótipo e correção, que é uma forma de atacar um problema complexo começando com um protótipo simples e lidando com as complicações de forma incremental.
Aqui está um protótipo simples de add_time:
def add_time(t1, t2):
sum = Time()
sum.hour = t1.hour + t2.hour
sum.minute = t1.minute + t2.minute
sum.second = t1.second + t2.second
return sum
A função cria um novo objeto Time, inicializa seus atributos e retorna uma referência ao novo objeto. A função pura é chamada assim porque não altera nenhum dos objetos passados a ela como argumentos; além disso, ela não tem efeitos, como exibir um valor ou receber entradas de usuário, apenas retorna um valor.
Para testar esta função, criarei objetos Time: start, que contém o tempo de início de um filme, como Monty Python e o cálice sagrado, e duration, que contém o tempo de execução do filme, que é de 1 hora e 35 minutos.
add_time calcula quando o filme acaba:
>>> start = Time()
>>> start.hour = 9
>>> start.minute = 45
>>> start.second = 0
>>> duration = Time()
>>> duration.hour = 1
>>> duration.minute = 35
>>> duration.second = 0
>>> done = add_time(start, duration)
>>> print_time(done)
10:80:00
O resultado, 10:80:00, pode não ser o que você esperava. O problema é que esta função não trata casos onde o número de segundos ou minutos é maior que 60. Quando isso acontece, precisamos transportar os segundos extras à coluna dos minutos ou os minutos extras à coluna das horas.
Aqui está uma versão melhorada:
def add_time(t1, t2):
sum = Time()
sum.hour = t1.hour + t2.hour
sum.minute = t1.minute + t2.minute
sum.second = t1.second + t2.second
if sum.second >= 60:
sum.second -= 60
sum.minute += 1
if sum.minute >= 60:
sum.minute -= 60
sum.hour += 1
return sum
Embora esta função esteja correta, é um pouco extensa. Veremos uma alternativa menor mais adiante.
16.3 - Modificadores
Às vezes é útil uma função alterar os objetos que recebe como parâmetros. Nesse caso, as mudanças são visíveis a quem chama a função. As funções que fazem isso chamam-se modificadores.
increment, que acrescenta um dado número de segundos a um objeto Time, pode ser escrita naturalmente como um modificador. Aqui está um primeiro esboço:
def increment(time, seconds):
time.second += seconds
if time.second >= 60:
time.second -= 60
time.minute += 1
if time.minute >= 60:
time.minute -= 60
time.hour += 1
A primeira linha executa a operação básica; o resto lida com os casos especiais que vimos antes.
Esta função está correta? O que acontece se second for muito mais que 60?
Neste caso não basta transportar uma vez, temos que continuar fazendo isso até que time.second seja menos de 60. Uma solução é substituir a instrução if pela instrução while. Isso tornaria a função correta, mas não muito eficiente. Como exercício, escreva uma versão correta de increment que não contenha loops.
O que se faz com modificadores também pode ser feito com funções puras. Na verdade, algumas linguagens de programação só permitem funções puras. Há evidências de que os programas que usam funções puras são mais rápidos para serem desenvolvidos e menos propensos a erros que programas que usam modificadores. No entanto, modificadores são convenientes de vez em quando, e os programas funcionais tendem a ser menos eficientes.
De forma geral, recomendo que você escreva funções puras sempre que achar razoável e recorra a modificadores só se houver alguma vantagem clara. Esta abordagem pode ser chamada de programação funcional.
Como exercício, escreva uma versão “pura” de increment que cria e retorna um objeto Time em vez de alterar o parâmetro.
16.4 - Prototipação versus planejamento
O plano de desenvolvimento que estou demonstrando chama-se “protótipo e correção”. Para cada função, escrevi um protótipo que executa o cálculo básico e então testa a função, corrigindo erros no decorrer do caminho.
Esta abordagem pode ser eficaz, especialmente se você ainda não tem uma compreensão profunda do problema. Porém, as correções incrementais podem gerar código que se complica desnecessariamente (pois trata de muitos casos especiais) e pouco confiáveis (já que é difícil saber se todos os erros foram encontrados).
Uma alternativa é o desenvolvimento planejado, no qual a compreensão de alto nível do problema pode facilitar muito a programação. Neste caso, descobre-se que um objeto Time é, na verdade, um número de três dígitos na base 60 (veja http://en.wikipedia.org/wiki/Sexagesimal)! O atributo second é a “coluna de unidades”, o atributo minute é a “coluna dos 60”, e o atributo hour é a “coluna do 3.600”.
Quando escrevemos add_time e increment, estávamos na verdade fazendo adições na base 60, e por isso transportávamos os resultados de uma coluna à seguinte.
Essa observação sugere outra abordagem para o problema inteiro – podemos converter objetos Time em números inteiros e aproveitar o fato de que o computador sabe trabalhar com aritmética de números inteiros.
Aqui está uma função que converte objetos Time em números inteiros:
def time_to_int(time):
minutes = time.hour * 60 + time.minute
seconds = minutes * 60 + time.second
return seconds
E aqui está uma função que converte um número inteiro em um Time (lembre-se de que divmod divide o primeiro argumento pelo segundo e devolve o quociente e o resto como uma tupla):
def int_to_time(seconds):
time = Time()
minutes, time.second = divmod(seconds, 60)
time.hour, time.minute = divmod(minutes, 60)
return time
Você pode ter que pensar um pouco e fazer alguns testes, para se convencer de que essas funções estão corretas. Um modo de testá-las é ver se time_to_int(int_to_time(x)) == x para muitos valores de x. Este é um exemplo de uma verificação de consistência.
Uma vez que esteja convencido de que estão corretas, você pode usá-las para reescrever add_time:
def add_time(t1, t2):
seconds = time_to_int(t1) + time_to_int(t2)
return int_to_time(seconds)
Esta versão é mais curta que a original, e mais fácil de verificar. Como exercício, reescreva increment usando time_to_int e int_to_time.
Em algumas situações, converter da base 60 para a base 10 e de volta é mais difícil que apenas lidar com as horas. A conversão de base é mais abstrata; nossa intuição para lidar com valores temporais é melhor.
No entanto, se tivermos discernimento para lidar com horas como números de base 60 e investirmos esforço em escrever as funções de conversão (time_to_int e int_to_time), chegamos a um programa que é mais curto, mais fácil de ler e depurar, e mais confiável.
Também é mais fácil acrescentar recursos depois. Por exemplo, imagine subtrair dois objetos Time para encontrar a duração entre eles. Uma abordagem ingênua seria implementar a subtração com transporte. Porém, usar funções de conversão seria mais fácil e, provavelmente, mais correto.
Ironicamente, tornar um problema mais difícil (ou mais geral) facilita (porque há menos casos especiais e menos oportunidades de erro).
16.5 - Depuração
Um objeto Time é bem formado se os valores de minute e second estiverem entre 0 e 60 (incluindo 0, mas não 60) e se hour for positivo. hour e minute devem ser valores inteiros, mas podemos permitir que second tenha uma parte fracionária.
Requisitos como esses chamam-se invariáveis porque sempre devem ser verdadeiros. Para dizer de outra forma, se não forem verdadeiros, algo deu errado.
Escrever código para verificar requisitos invariáveis pode ajudar a descobrir erros e encontrar suas causas. Por exemplo, você pode ter uma função como valid_time, que receba um objeto Time e retorne False se ele violar um requisito invariável:
def valid_time(time):
if time.hour < 0 or time.minute < 0 or time.second < 0:
return False
if time.minute >= 60 or time.second >= 60:
return False
return True
No início de cada função você pode verificar os argumentos para ter certeza de que são válidos:
def add_time(t1, t2):
if not valid_time(t1) or not valid_time(t2):
raise ValueError('invalid Time object in add_time')
seconds = time_to_int(t1) + time_to_int(t2)
return int_to_time(seconds)
Ou você pode usar uma instrução assert, que verifica determinado requisito invariável e cria uma exceção se ela falhar:
def add_time(t1, t2):
assert valid_time(t1) and valid_time(t2)
seconds = time_to_int(t1) + time_to_int(t2)
return int_to_time(seconds)
Instruções assert são úteis porque distinguem o código que lida com condições normais do código que verifica erros.
16.6 - Glossário
protótipo e correção
Plano de desenvolvimento no qual a escrita do programa parte de um esboço inicial, e depois segue ao teste e correção de erros, conforme sejam encontrados.
desenvolvimento planejado
Plano de desenvolvimento que implica uma compreensão de alto nível do problema e mais planejamento que desenvolvimento incremental ou desenvolvimento prototipado.
função pura
Função que não altera nenhum dos objetos que recebe como argumento. A maior parte das funções puras gera resultado.
modificador
Função que modifica um ou vários dos objetos que recebe como argumento. A maior parte dos modificadores são nulos; isto é, retornam None.
programação funcional
Estilo de projeto de programa no qual a maioria das funções são puras.
invariável
Condição que sempre deve ser verdadeira durante a execução de um programa.
instrução assert
Instrução que verifica uma condição e levanta uma exceção se esta falhar.
16.7 - Exercícios
Os exemplos de código deste capítulo estão disponíveis em http://thinkpython2.com/code/Time1.py; as soluções para os exercícios estão disponíveis em http://thinkpython2.com/code/Time1_soln.py.
Exercício 16.1
Escreva uma função chamada mul_time que receba um objeto Time e um número e retorne um novo objeto Time que contenha o produto do Time original e do número.
Então use mul_time para escrever uma função que receba um objeto Time representando o tempo até o fim de uma corrida e um número que represente a distância, e retorne um objeto Time com o passo médio (tempo por milha).
Exercício 16.2
O módulo datetime fornece objetos time que são semelhantes aos objetos Time deste capítulo, mas ele oferece um grande conjunto de métodos e operadores. Leia a documentação em http://docs.python.org/3/library/datetime.html.
-
Use o módulo
datetimepara escrever um programa que receba a data atual e exiba o dia da semana. -
Escreva um programa que receba um aniversário como entrada e exiba a idade do usuário e o número de dias, horas, minutos e segundos até o seu próximo aniversário.
-
Para duas pessoas nascidas em dias diferentes, há um dia em que a idade de uma equivale a duas vezes a da outra. Este é o Dia Duplo delas. Escreva um programa que receba dois aniversários e calcule o Dia Duplo dos aniversariantes.
-
Para um desafio um pouco maior, escreva a versão mais geral que calcule o dia em que uma pessoa é N vezes mais velha que a outra.
Capítulo 17: Classes e métodos
Embora estejamos usando alguns recursos de orientação a objeto do Python, os programas dos dois últimos capítulos não são realmente orientados a objeto, porque não representam as relações entre os tipos definidos pelo programador e as funções que os produzem. O próximo passo é transformar essas funções em métodos que tornem as relações claras.
Os exemplos de código deste capítulo estão disponíveis em http://thinkpython2.com/code/Time2.py e as soluções para os exercícios estão em http://thinkpython2.com/code/Point2_soln.py.
17.1 - Recursos de orientação a objeto
Python é uma linguagem de programação orientada a objeto, ou seja, ela oferece recursos de programação orientada a objeto que tem a seguintes características:
-
Os programas incluem definições de classes e métodos.
-
A maior parte dos cálculos é expressa em termos de operações em objetos.
-
Os objetos muitas vezes representam coisas no mundo real, e os métodos muitas vezes correspondem às formas em que as coisas no mundo real interagem.
Por exemplo, a classe Time definida no Capítulo 16 corresponde à forma como as pessoas registram a hora do dia, e as funções que definimos correspondem aos tipos de coisas que as pessoas fazem com os horários. De forma similar, as classes Point e Rectangle no Capítulo 15 correspondem aos conceitos matemáticos de ponto e retângulo.
Por enquanto, não aproveitamos os recursos que o Python oferece para programação orientada a objeto. Esses recursos não são estritamente necessários; a maioria deles oferece uma sintaxe alternativa para coisas que já fizemos. No entanto, em muitos casos, a alternativa é mais concisa e representa de forma mais exata a estrutura do programa.
Por exemplo, em Time1.py não há nenhuma conexão óbvia entre a definição de classe e as definições de função que seguem. Com um pouco de atenção, é evidente que cada função recebe pelo menos um objeto Time como argumento.
Essa observação é a motivação para usar métodos; um método é uma função associada a determinada classe. Vimos métodos de string, listas, dicionários e tuplas. Neste capítulo definiremos métodos para tipos definidos pelo programador.
Métodos são semanticamente o mesmo que funções, mas há duas diferenças sintáticas:
-
Os métodos são definidos dentro de uma definição de classe para tornar clara a relação entre a classe e o método.
-
A sintaxe para invocar um método é diferente da sintaxe para chamar uma função.
Nas próximas seções tomaremos as funções dos dois capítulos anteriores e as transformaremos em métodos. Essa transformação é puramente mecânica; você pode fazê-la seguindo uma série de passos. Se estiver à vontade para fazer a conversão entre uma forma e outra, sempre poderá escolher a melhor forma para contemplar os seus objetivos.
17.2 - Exibição de objetos
No Capítulo 16 definimos uma classe chamada Time em “Time”, na página 231, e você escreveu uma função denominada print_time:
class Time:
"""Represents the time of day."""
def print_time(time):
print('%.2d:%.2d:%.2d' % (time.hour, time.minute, time.second))
Para chamar esta função, você precisa passar um objeto Time como argumento:
>>> start = Time()
>>> start.hour = 9
>>> start.minute = 45
>>> start.second = 00
>>> print_time(start)
09:45:00
Para fazer de print_time um método, tudo o que precisamos fazer é mover a definição da função para dentro da definição da classe. Note a alteração na endentação:
class Time:
def print_time(time):
print('%.2d:%.2d:%.2d' % (time.hour, time.minute, time.second))
Agora há duas formas de chamar print_time. A primeira forma (e menos comum) é usar a sintaxe de função:
>>> Time.print_time(start)
09:45:00
Nesse uso da notação de ponto, Time é o nome da classe, e print_time é o nome do método. start é passado como um parâmetro.
A segunda forma (e mais concisa) é usar a sintaxe de método:
>>> start.print_time()
09:45:00
Nesse uso da notação de ponto, print_time é o nome do método (novamente), e start é o objeto no qual o método é invocado, que se chama de sujeito. Assim como em uma sentença, onde o sujeito é o foco da escrita, o sujeito de uma invocação de método é o foco do método.
Dentro do método, o sujeito é atribuído ao primeiro parâmetro, portanto, neste caso, start é atribuído a time.
Por convenção, o primeiro parâmetro de um método chama-se self, então seria mais comum escrever print_time desta forma:
class Time:
def print_time(self):
print('%.2d:%.2d:%.2d' % (self.hour, self.minute, self.second))
A razão dessa convenção é uma metáfora implícita:
-
A sintaxe de uma chamada de função,
print_time(start), sugere que a função é o agente ativo. Ela diz algo como: “Ei,print_time! Aqui está um objeto para você exibir”. -
Na [programação orientada a objeto](12-glossario.md#programação-orientada a-objeto), os objetos são os agentes ativos. Uma invocação de método
como start.print_time()diz: “Ei,start! Por favor, exiba-se”.
Essa mudança de perspectiva pode ser mais polida, mas não é óbvio que seja útil. Nos exemplos que vimos até agora, pode não ser. Porém, às vezes, deslocar a responsabilidade das funções para os objetos permite escrever funções (ou métodos) mais versáteis e facilita a manutenção e reutilização do código.
Como exercício, reescreva time_to_int (de “Prototipação versus planejamento”, na página 234) como um método. Você pode ficar tentado a reescrever int_to_time como um método também, mas isso não faz muito sentido porque não haveria nenhum objeto sobre o qual invocá-lo.
17.3 - Outro exemplo
Aqui está uma versão de increment (de “Modificadores”, na página 233) reescrita como método:
# dentro da classe Time:
def increment(self, seconds):
seconds += self.time_to_int()
return int_to_time(seconds)
Essa versão assume que time_to_int seja escrita como método. Além disso, observe que é uma função pura, não um modificador.
É assim que eu invocaria increment:
>>> start.print_time()
09:45:00
>>> end = start.increment(1337)
>>> end.print_time()
10:07:17
O sujeito, start, é atribuído ao primeiro parâmetro, self. O argumento, 1337, é atribuído ao segundo parâmetro, seconds.
Esse mecanismo pode ser confuso, especialmente se você fizer um erro. Por exemplo, se invocar increment com dois argumentos, recebe:
>>> end = start.increment(1337, 460)
TypeError: increment() takes 2 positional arguments but 3 were given
A mensagem de erro é inicialmente confusa, porque há só dois argumentos entre parênteses. No entanto, o sujeito também é considerado um argumento, então, somando tudo, são três.
A propósito, um argumento posicional é o que não tem um nome de parâmetro; isto é, não é um argumento de palavra-chave. Nesta chamada da função:
sketch(parrot, cage, dead=True)
parrot e cage são posicionais, e dead é um argumento de palavra-chave.
17.4 - Um exemplo mais complicado
Reescrever is_after (de “Time”, na página 231) é ligeiramente mais complicado, porque ela recebe dois objetos Time como parâmetros. Nesse caso, a convenção é denominar o primeiro parâmetro self e o segundo parâmetro other:
# dentro da classe Time:
def is_after(self, other):
return self.time_to_int() > other.time_to_int()
Para usar este método, você deve invocá-lo para um objeto e passar outro como argumento:
>>> end.is_after(start)
True
Uma vantagem desta sintaxe é que é quase literal em inglês: “o fim é depois da partida?”.
17.5 - Método init
O método __init__ (abreviação da palavra em inglês para “inicialização”) é um método especial, invocado quando um objeto é instanciado. Seu nome completo é __init__ (dois caracteres de sublinhado, seguidos de init, e mais dois sublinhados). Um método __init__ da classe Time pode ser algo assim:
# dentro da classe Time:
def __init__(self, hour=0, minute=0, second=0):
self.hour = hour
self.minute = minute
self.second = second
É comum que os parâmetros de __init__ tenham os mesmos nomes que os atributos. A instrução
self.hour = hour
guarda o valor do parâmetro hour como um atributo de self.
Os parâmetros são opcionais, então, se você chamar Time sem argumentos, recebe os valores padrão:
>>> time = Time()
>>> time.print_time()
00:00:00
Se incluir um argumento, ele define hour.
>>> time = Time (9)
>>> time.print_time()
09:00:00
Se fornecer dois argumentos, hour e minute serão definidos:
>>> time = Time(9, 45)
>>> time.print_time()
09:45:00
E se você fornecer três argumentos, os três valores serão definidos.
Como exercício, escreva um método init da classe Point que receba x e y como parâmetros opcionais e os relacione aos atributos correspondentes.
17.6 - Método __str__
__str__ é um método especial, como __init__, usado para retornar uma representação de string de um objeto.
Por exemplo, aqui está um método str para objetos Time:
# dentro da classe Time:
def __str__(self):
return '%.2d:%.2d:%.2d' % (self.hour, self.minute, self.second)
Ao exibir um objeto com print, o Python invoca o método str:
>>> time = Time(9, 45)
>>> print(time)
09:45:00
Quando escrevo uma nova classe, quase sempre começo escrevendo __init__, o que facilita a instanciação de objetos, e __str__, que é útil para a depuração.
Como exercício, escreva um método str da classe Point. Crie um objeto Point e exiba-o.
17.7 - Sobrecarga de operadores
Ao definir outros métodos especiais, você pode especificar o comportamento de operadores nos tipos definidos pelo programador. Por exemplo, se você definir um método chamado __add__ para a classe Time de Time, pode usar o operador + em objetos Time.
A definição pode ser assim:
# dentro da classe Time:
def __add__(self, other):
seconds = self.time_to_int() + other.time_to_int()
return int_to_time(seconds)
Você pode usá-lo assim:
>>> start = Time(9, 45)
>>> duration = Time(1, 35)
>>> print(start + duration)
11:20:00
Ao aplicar o operador + a objetos Time, o Python invoca __add__. Ao exibir o resultado, o Python invoca __str__. Ou seja, há muita coisa acontecendo nos bastidores!
Alterar o comportamento de um operador para que funcione com tipos definidos pelo programador chama-se sobrecarga de operadores. Para cada operador no Python há um método especial correspondente, como __add__. Para obter mais informações, veja http://docs.python.org/3/reference/datamodel.html#specialnames.
Como exercício, escreva um método add para a classe Point.
17.8 - Despacho por tipo
Na seção anterior, acrescentamos dois objetos Time, mas você também pode querer acrescentar um número inteiro a um objeto Time. A seguir, veja uma versão de __add__, que verifica o tipo de other e invoca add_time ou increment:
# dentro da classe Time:
def __add__(self, other):
if isinstance(other, Time):
return self.add_time(other)
else:
return self.increment(other)
def add_time(self, other):
seconds = self.time_to_int() + other.time_to_int()
return int_to_time(seconds)
def increment(self, seconds):
seconds += self.time_to_int()
return int_to_time(seconds)
A função construída isinstance recebe um valor e um objeto de classe e retorna True se o valor for uma instância da classe.
Se other for um objeto Time, __add__ invoca add_time. Do contrário, assume que o parâmetro seja um número e invoca increment. Essa operação chama-se despacho por tipo porque despacha a operação a métodos diferentes, baseados no tipo dos argumentos.
Veja exemplos que usam o operador + com tipos diferentes:
>>> start = Time(9, 45)
>>> duration = Time(1, 35)
>>> print(start + duration)
11:20:00
>>> print(start + 1337)
10:07:17
Infelizmente, esta implementação da adição não é comutativa. Se o número inteiro for o primeiro operando, você recebe
>>> print(1337 + start)
TypeError: unsupported operand type(s) for +: 'int' and 'instance'
O problema é que, em vez de pedir ao objeto Time que adicione um número inteiro, o Python está pedindo que um número inteiro adicione um objeto Time, e ele não sabe como fazer isso. Entretanto, há uma solução inteligente para este problema: o método especial __radd__, que significa “adição à direita”. Esse método é invocado quando um objeto Time aparece no lado direito do operador +. Aqui está a definição:
# dentro da classe Time:
def __radd__(self, other):
return self.__add__(other)
E é assim que ele é usado:
>>> print(1337 + start)
10:07:17
Como exercício, escreva um método add para Points que funcione com um objeto Point ou com uma tupla:
-
Se o segundo operando for um Point, o método deve retornar um novo Point cuja coordenada x é a soma das coordenadas x dos operandos, e o mesmo se aplica às coordenadas de y.
-
Se o segundo operando for uma tupla, o método deve adicionar o primeiro elemento da tupla à coordenada de x e o segundo elemento à coordenada de y, retornando um novo Point com o resultado.
17.9 - Polimorfismo
O despacho por tipo é útil, mas (felizmente) nem sempre é necessário. Muitas vezes, você pode evitá-lo escrevendo funções que funcionem corretamente para argumentos de tipos diferentes.
Muitas das funções que escrevemos para strings também funcionam para outros tipos de sequência. Por exemplo, em “Um dicionário como uma coleção de contadores”, na página 163, usamos histogram para contar o número de vezes que cada letra aparece numa palavra:
def histogram(s):
d = dict()
for c in s:
if c not in d:
d[c] = 1
else:
d[c] = d[c] + 1
return d
Essa função também funciona com listas, tuplas e até dicionários, desde que os elementos de s sejam hashable, então eles podem ser usados como chaves em d:
>>> t = ['spam', 'egg', 'spam', 'spam', 'bacon', 'spam']
>>> histogram(t)
{'bacon': 1, 'egg': 1, 'spam': 4}
As funções que funcionam com vários tipos chamam-se polimórficas. O polimorfismo pode facilitar a reutilização do código. Por exemplo, a função integrada sum, que adiciona os elementos de uma sequência, funciona só se os elementos da sequência forem compatíveis com adição.
Como os objetos Time oferecem o método add, eles funcionam com sum:
>>> t1 = Time(7, 43)
>>> t2 = Time(7, 41)
>>> t3 = Time(7, 37)
>>> total = sum([t1, t2, t3])
>>> print(total)
23:01:00
Em geral, se todas as operações dentro de uma função forem compatíveis com um dado tipo, não haverá problemas.
O melhor tipo de polimorfismo é o não intencional, quando você descobre que uma função que já escreveu pode ser aplicada a um tipo para o qual ela não tinha planejada.
17.10 - Interface e implementação
Uma das metas do projeto orientado a objeto é facilitar a manutenção do programa, para que você possa mantê-lo funcionando quando outras partes do sistema forem alteradas, e também poder alterar o programa para satisfazer novas condições.
Um princípio de projeto que ajuda a atingir essa meta é manter as interfaces separadas das implementações. Para objetos, isso quer dizer que os métodos que uma classe oferece não devem depender de como os atributos são representados.
Por exemplo, neste capítulo desenvolvemos uma classe que representa uma hora do dia. Os métodos fornecidos por esta classe incluem time_to_int, is_after e add_time.
Podemos implementar esses métodos de várias formas. Os detalhes da implementação dependem de como representamos as horas. Neste capítulo, os atributos de um objeto Time são hour, minute e second.
Como alternativa, podemos substituir esses atributos por um número inteiro único que represente o número de segundos desde a meia-noite. Essa implementação faria com que alguns métodos, como is_after, fossem mais fáceis de escrever, mas dificultaria o uso de outros métodos.
Pode acontecer que, depois de implementar uma nova classe, você descubra uma implementação melhor. Se outras partes do programa estiverem usando a sua classe, mudar a interface pode ser trabalhoso e induzir a erros.
No entanto, se projetou a interface cuidadosamente, pode alterar a implementação sem mudar a interface, e não será preciso mudar outras partes do programa.
17.11 - Depuração
É legal acrescentar atributos a objetos em qualquer ponto da execução de um programa, mas se você tiver objetos do mesmo tipo que não têm os mesmos atributos, é fácil cometer erros. É uma boa ideia inicializar todos os atributos de um objeto no método init.
Caso não tenha certeza se um objeto tem um determinado atributo, você pode usar a função integrada hasattr (ver “Depuração”, na página 236).
Outra forma de acessar atributos é com a função integrada vars, que recebe um objeto e retorna um dicionário que mapeia os nomes dos atributos (como strings) aos seus valores:
>>> p = Point(3, 4)
>>> vars(p)
{'y': 4, 'x': 3}
Para facilitar a depuração, pode ser útil usar esta função:
def print_attributes(obj):
for attr in vars(obj):
print(attr, getattr(obj, attr))
print_attributes atravessa o dicionário e imprime cada nome de atributo e o seu valor correspondente.
A função integrada getattr recebe um objeto e um nome de atributo (como uma string) e devolve o valor do atributo.
17.12 - Glossário
linguagem orientada a objeto
Linguagem que fornece recursos, como tipos definidos pelo programador e métodos, que facilitam a programação orientada a objeto.
programação orientada a objeto
Estilo de programação na qual os dados e as operações que os manipulam são organizadas em classes e métodos.
método
Função criada dentro de uma definição de classe e invocada em instâncias desta classe.
sujeito
Objeto sobre o qual um método é invocado.
argumento posicional
Argumento que não inclui um nome de parâmetro, portanto não é um argumento de palavra-chave.
sobrecarga de operador
Alteração do comportamento de um operador como + para que funcione com um tipo definido pelo programador.
despacho por tipo
Modelo de programação que invoca funções diferentes dependendo do tipo do operando.
polimórfico
Pertinente a uma função que pode funcionar com mais de um tipo.
ocultamento de informação
Princípio segundo o qual a interface fornecida por um objeto não deve depender da sua implementação, especialmente em relação à representação dos seus atributos.
17.13 - Exercícios
Exercício 17.1
Baixe o código deste capítulo em http://thinkpython2.com/code/Time2.py. Altere os atributos de Time para que um número inteiro único represente os segundos decorridos desde a meia-noite. Então altere os métodos (e a função int_to_time) para funcionar com a nova implementação. Você não deve modificar o código de teste em main. Ao terminar, a saída deve ser a mesma que antes.
Solução: http://thinkpython2.com/code/Time2_soln.py.
Exercício 17.2
Este exercício é uma história com moral sobre um dos erros mais comuns e difíceis de encontrar no Python. Escreva uma definição de classe chamada Kangaroo com os seguintes métodos:
-
Um método
__init__que inicialize um atributo chamadopouch_contentsem uma lista vazia. -
Um método chamado
put_in_pouchque receba um objeto de qualquer tipo e o acrescente apouch_contents. -
Um método
__str__que retorne uma representação de string do objeto Kangaroo e os conteúdos de pouch (bolsa).
Teste o seu código criando dois objetos Kangaroo, atribuindo-os a variáveis chamadas kanga e roo, e então acrescentando roo ao conteúdo da bolsa de kanga.
Baixe http://thinkpython2.com/code/BadKangaroo.py. Ele contém uma solução para o problema anterior com um defeito bem grande e bem feio. Encontre e corrija o defeito.
Se não conseguir achar a solução, você pode baixar http://thinkpython2.com/code/GoodKangaroo.py, que explica o problema e demonstra uma solução.
Capítulo 18: Herança
O termo mais associado com a programação orientada a objeto é herança. A herança é a capacidade de definir uma nova classe que seja uma versão modificada de uma classe existente. Neste capítulo demonstrarei a herança usando classes que representam jogos de cartas, baralhos e mãos de pôquer.
Se você não joga pôquer, pode ler sobre ele em http://en.wikipedia.org/wiki/Poker, mas não é necessário; vou dizer tudo o que precisa saber para os exercícios.
Os exemplos de código deste capítulo estão disponíveis em http://thinkpython2.com/code/Card.py.
18.1 - Objetos Card
Há 52 cartas em um baralho, e cada uma pertence a 1 dos 4 naipes e a 1 dos 13 valores. Os naipes são espadas, copas, ouros e paus (no bridge, em ordem descendente). A ordem dos valores é ás, 2, 3, 4, 5, 6, 7, 8, 9, 10, valete, dama e rei. Dependendo do jogo que estiver jogando, um ás pode ser mais alto que o rei ou mais baixo que 2.
Se quiséssemos definir um novo objeto para representar uma carta de jogo, os atributos óbvios seriam rank (valor) e suit (naipe). Mas não é tão óbvio qual tipo de atributo deveriam ser. Uma possibilidade é usar strings com palavras como 'Spade' (Espadas) para naipes e 'Queen' (Dama) para valores. Um problema com esta implementação é que não seria fácil comparar cartas para ver qual valor ou naipe tem classificação mais alta em relação aos outros.
Uma alternativa é usar números inteiros para codificar os valores e os naipes. Neste contexto, “codificar” significa que vamos definir um mapeamento entre números e naipes, ou entre números e valores. Este tipo de codificação não tem nada a ver com criptografia.
Por exemplo, esta tabela mostra os naipes e os códigos de número inteiro correspondentes:
Spades (Espadas) ↦ 3
Hearts (Copas) ↦ 2
Diamonds (Ouros) ↦ 1
Clubs (Paus) ↦ 0
Este código facilita a comparação entre as cartas; como naipes mais altos mapeiam a números mais altos, podemos comparar naipes aos seus códigos.
O mapeamento de valores é até óbvio; cada um dos valores numéricos é mapeado ao número inteiro correspondente, e para cartas com figuras:
Jack (Valete) ↦ 11
Queen (Dama) ↦ 12
King (Rei) ↦ 13
Estou usando o símbolo ↦ para deixar claro que esses mapeamentos não são parte do programa em Python. Eles são parte do projeto do programa, mas não aparecem explicitamente no código.
A definição de classe para Card (carta) é assim:
class Card:
"""Represents a standard playing card."""
def __init__(self, suit=0, rank=2):
self.suit = suit
self.rank = rank
Como sempre, o método __init__ recebe um parâmetro opcional de cada atributo. A carta padrão é 2 de paus.
Para criar um Card, você chama Card com o naipe e valor desejados:
queen_of_diamonds = Card(1, 12)
18.2 - Atributos de classe
Para exibir objetos Card de uma forma que as pessoas possam ler com facilidade, precisamos de um mapeamento dos códigos de número inteiro aos naipes e valores correspondentes. Uma forma natural de fazer isso é com listas de strings. Atribuímos essas listas a atributos de classe:
# dentro da classe Card:
suit_names = ['Clubs', 'Diamonds', 'Hearts', 'Spades']
rank_names = [None, 'Ace', '2', '3', '4', '5', '6', '7',
'8', '9', '10', 'Jack', 'Queen', 'King']
def __str__(self):
return '%s of %s' % (Card.rank_names[self.rank],
Card.suit_names[self.suit])
Variáveis como suit_names e rank_names, que são definidas dentro de uma classe, mas fora de qualquer método, chamam-se atributos de classe porque são associadas com o objeto de classe Card.
Este termo as distingue de variáveis como suit e rank, chamadas de atributos de instância porque são associados com determinada instância.
Ambos os tipos de atributo são acessados usando a notação de ponto. Por exemplo, em __str__, self é um objeto Card, e self.rank é o seu valor. De forma semelhante, Card é um objeto de classe, e Card.rank_names é uma lista de strings associadas à essa classe.
Cada carta tem seu próprio suit e rank, mas há só uma cópia de suit_names e rank_names.
Juntando tudo, a expressão Card.rank_names[self.rank] significa “use o rank (valor) do atributo do objeto self como um índice na lista rank_names da classe Card e selecione a string adequada”.
O primeiro elemento de rank_names é None, porque não há nenhuma carta com valor zero. Incluindo None para ocupar uma variável, conseguimos fazer um belo mapeamento onde o índice 2 é associado à string '2', e assim por diante. Para evitar ter que usar esse truque, poderíamos usar um dicionário em vez de uma lista.
Com os métodos que temos por enquanto, podemos criar e exibir cartas:
>>> card1 = Card(2, 11)
>>> print(card1)
Jack of Hearts
A Figura 18.1 é um diagrama do objeto de classe Card e uma instância de Card. Card é um objeto de classe; seu tipo é type. card1 é uma instância de Card, então seu tipo é Card. Para economizar espaço, não incluí o conteúdo de suit_names e rank_names.
 .
.
Figura 18.1 – Diagrama de objetos: classe Card e card1, uma instância de Card.
18.3 - Comparação de cartas
Para tipos integrados, há operadores relacionais (<, >, == etc) que comparam valores e determinam quando um é maior, menor ou igual a outro. Para tipos definidos pelo programador, podemos ignorar o comportamento dos operadores integrados fornecendo um método denominado __lt__, que representa “menos que”.
__lt__ recebe dois parâmetros, self e other, e True se self for estritamente menor que other.
A ordem correta das cartas não é óbvia. Por exemplo, qual é melhor, o 3 de paus ou o 2 de ouros? Uma tem o valor mais alto, mas a outra tem um naipe mais alto. Para comparar cartas, é preciso decidir o que é mais importante, o valor ou o naipe.
A resposta pode depender de que jogo você está jogando, mas, para manter a simplicidade, vamos fazer a escolha arbitrária de que o naipe é mais importante, então todas as cartas de espadas são mais importantes que as de ouros, e assim por diante.
Com isto decidido, podemos escrever __lt__:
# dentro da classe Card:
def __lt__(self, other):
# conferir os naipes
if self.suit < other.suit: return True
if self.suit > other.suit: return False
# os naipes são os mesmos... conferir valores
return self.rank < other.rank
Você pode escrever isso de forma mais concisa usando uma comparação de tuplas:
# dentro da classe Card:
def __lt__(self, other):
t1 = self.suit, self.rank
t2 = other.suit, other.rank
return t1 < t2
Como exercício, escreva um método __lt__ para objetos Time. Você pode usar uma comparação de tuplas, mas também pode usar a comparação de números inteiros.
18.4 - Baralhos
Agora que temos Card, o próximo passo é definir Deck (baralho). Como um baralho é composto de cartas, é natural que um baralho contenha uma lista de cartas como atributo.
Veja a seguir uma definição de classe para Deck. O método init cria o atributo cards e gera o conjunto padrão de 52 cartas:
class Deck:
def __init__(self):
self.cards = []
for suit in range(4):
for rank in range(1, 14):
card = Card(suit, rank)
self.cards.append(card)
A forma mais fácil de preencher o baralho é com um loop aninhado. O loop exterior enumera os naipes de 0 a 3. O loop interior enumera os valores de 1 a 13. Cada iteração cria um novo Card com o naipe e valor atual, e a acrescenta a self.cards.
18.5 - Exibição do baralho
Aqui está um método str para Deck:
# dentro da classe Deck:
def __str__(self):
res = []
for card in self.cards:
res.append(str(card))
return '\n'.join(res)
Este método demonstra uma forma eficiente de acumular uma string grande: a criação de uma lista de strings e a utilização do método de string join. A função integrada str invoca o método __str__ em cada carta e retorna a representação da string.
Como invocamos join em um caractere newline, as cartas são separadas por quebras de linha. O resultado é esse:
>>> deck = Deck()
>>> print(deck)
Ace of Clubs
2 of Clubs
3 of Clubs
...
10 of Spades
Jack of Spades
Queen of Spades
King of Spades
Embora o resultado apareça em 52 linhas, na verdade ele é uma string longa com quebras de linha.
18.6 - Adição, remoção, embaralhamento e classificação
Para lidar com as cartas, gostaríamos de ter um método que removesse uma carta do baralho e a devolvesse. O método de lista pop oferece uma forma conveniente de fazer isso:
# dentro da classe Deck:
def pop_card(self):
return self.cards.pop()
Como pop retira a última carta na lista, estamos lidando com o fundo do baralho.
Para adicionar uma carta, podemos usar o método de lista append:
# dentro da classe Deck:
def add_card(self, card):
self.cards.append(card)
Um método como esse, que usa outro método sem dar muito trabalho, às vezes é chamado de folheado. A metáfora vem do trabalho em madeira, onde o folheado é uma camada fina de madeira de boa qualidade colada à superfície de uma madeira mais barata para melhorar a aparência.
Nesse caso, add_card é um método “fino” que expressa uma operação de lista em termos adequados a baralhos. Ele melhora a aparência ou interface da implementação.
Em outro exemplo, podemos escrever um método Deck denominado shuffle, usando a função shuffle do módulo random:
# dentro da classe Deck:
def shuffle(self):
random.shuffle(self.cards)
Não se esqueça de importar random.
Como exercício, escreva um método de Deck chamado sort, que use o método de lista sort para classificar as cartas em um Deck. sort usa o método __lt__ que definimos para determinar a ordem.
18.7 - Herança
A herança é a capacidade de definir uma nova classe que seja uma versão modificada de uma classe existente. Como exemplo, digamos que queremos que uma classe represente uma “mão”, isto é, as cartas mantidas por um jogador. Uma mão é semelhante a um baralho: ambos são compostos por uma coleção de cartas, e ambos exigem operações como adicionar e remover cartas.
Uma mão também é diferente de um baralho; há operações que queremos para mãos que não fazem sentido para um baralho. Por exemplo, no pôquer poderíamos comparar duas mãos para ver qual ganha. No bridge, poderíamos calcular a pontuação de uma mão para fazer uma aposta.
Essa relação entre classes – semelhante, mas diferente – adequa-se à herança. Para definir uma nova classe que herda algo de uma classe existente, basta colocar o nome da classe existente entre parênteses:
class Hand(Deck):
"""Represents a hand of playing cards."""
Esta definição indica que Hand herda de Deck; isso significa que podemos usar métodos como pop_card e add_card para Hand bem como para Deck.
Quando uma nova classe herda de uma existente, a existente chama-se pai e a nova classe chama-se filho.
Neste exemplo, Hand herda __init__ de Deck, mas na verdade não faz o que queremos: em vez de preencher a mão com 52 cartas novas, o método init de Hand deve inicializar card com uma lista vazia.
Se fornecermos um método init na classe Hand, ele ignora o da classe Deck:
# dentro da classe Hand:
def __init__(self, label=''):
self.cards = []
self.label = label
Ao criar Hand, o Python invoca este método init, não o de Deck.
>>> hand = Hand('new hand')
>>> hand.cards
[]
>>> hand.label
'new hand'
Outros métodos são herdados de Deck, portanto podemos usar pop_card e add_card para lidar com uma carta:
>>> deck = Deck()
>>> card = deck.pop_card()
>>> hand.add_card(card)
>>> print(hand)
King of Spades
Um próximo passo natural seria encapsular este código em um método chamado move_cards:
# dentro da classe Deck:
def move_cards(self, hand, num):
for i in range(num):
hand.add_card(self.pop_card())
move_cards recebe dois argumentos, um objeto Hand e o número de cartas com que vai lidar. Ele altera tanto self como hand e retorna None.
Em alguns jogos, as cartas são movidas de uma mão a outra, ou de uma mão de volta ao baralho. É possível usar move_cards para algumas dessas operações: self pode ser um Deck ou Hand, e hand, apesar do nome, também pode ser um Deck.
A herança é um recurso útil. Alguns programas que poderiam ser repetitivos sem herança podem ser escritos de forma mais elegante com ela. A herança pode facilitar a reutilização de código, já que você pode personalizar o comportamento de classes pais sem ter que alterá-las. Em alguns casos, a estrutura de herança reflete a estrutura natural do problema, o que torna o projeto mais fácil de entender.
De outro lado, a herança pode tornar os programas difíceis de ler. Quando um método é invocado, às vezes não está claro onde encontrar sua definição. O código relevante pode ser espalhado por vários módulos. Além disso, muitas das coisas que podem ser feitas usando a herança podem ser feitas sem elas, às vezes, até de forma melhor.
18.8 - Diagramas de classe
Por enquanto vimos diagramas de pilha, que mostram o estado de um programa e diagramas de objeto, que mostram os atributos de um objeto e seus valores. Esses diagramas representam um retrato da execução de um programa, então eles mudam no decorrer da execução do programa.
Eles também são altamente detalhados; para alguns objetivos, detalhados demais. Um diagrama de classe é uma representação mais abstrata da estrutura de um programa. Em vez de mostrar objetos individuais, ele mostra classes e as relações entre elas.
Há vários tipos de relações entre as classes:
-
Os objetos de uma classe podem conter referências a objetos em outra classe. Por exemplo, cada Rectangle contém uma referência a um Point, e cada Deck contém referências a muitos Cards. Esse tipo de relação chama-se composição. É uma relação do tipo HAS-A (tem um), com a ideia de “um Rectangle tem um Point”.
-
Uma classe pode herdar de outra. Esta relação chama-se IS-A (é um), com a ideia de “um Hand é um tipo de Deck”.
-
Uma classe pode depender de outra no sentido de que os objetos em uma classe possam receber objetos na segunda classe como parâmetros ou usar esses objetos como parte de um cálculo. Este tipo de relação chama-se dependência.
Um diagrama de classe é uma representação gráfica dessas relações. Por exemplo, a Figura 18.2 mostra as relações entre Card, Deck e Hand.
 .
.
Figura 18.2 – Diagrama de classes.
A flecha com um triângulo oco representa uma relação IS-A; nesse caso, indica que Hand herda de Deck.
A ponta de flecha padrão representa uma relação HAS-A; nesse caso, um Deck tem referências a objetos Card.
A estrela * perto da ponta de flecha indica a multiplicidade; ela indica quantos Cards um Deck tem. Uma multiplicidade pode ser um número simples como 52, um intervalo como 5..7 ou uma estrela, que indica que um Deck pode ter qualquer número de Cards.
Não há nenhuma dependência neste diagrama. Elas normalmente apareceriam com uma flecha tracejada. Ou, se houver muitas dependências, às vezes elas são omitidas.
Um diagrama mais detalhado poderia mostrar que um Deck na verdade contém uma lista de Cards, mas os tipos integrados como lista e dict não são normalmente incluídos em diagramas de classe.
18.9 - Encapsulamento de dados
Os capítulos anteriores demonstram um plano de desenvolvimento que poderíamos chamar de “projeto orientado a objeto”. Identificamos os objetos de que precisamos – como Point, Rectangle e Time – e definimos classes para representá-los. Em cada caso há uma correspondência óbvia entre o objeto e alguma entidade no mundo real (ou, pelo menos, no mundo matemático).
Mas, às vezes, é menos óbvio quais objetos você precisa e como eles devem interagir. Nesse caso é necessário um plano de desenvolvimento diferente. Da mesma forma em que descobrimos interfaces de função por encapsulamento e generalização, podemos descobrir interfaces de classe por encapsulamento de dados.
A análise de Markov, de “Análise de Markov”, na página 200, apresenta um bom exemplo. Se baixar o meu código em http://thinkpython2.com/code/markov.py, você vai ver que ele usa duas variáveis globais – suffix_map e prefix – que são lidas e escritas a partir de várias funções.
suffix_map = {}
prefix = ()
Como essas variáveis são globais, só podemos executar uma análise de cada vez. Se lermos dois textos, seus prefixos e sufixos seriam acrescentados às mesmas estruturas de dados (o que geraria textos interessantes).
Para executar análises múltiplas e guardá-las separadamente, podemos encapsular o estado de cada análise em um objeto. É assim que fica:
class Markov:
def __init__(self):
self.suffix_map = {}
self.prefix = ()
Em seguida, transformamos as funções em métodos. Por exemplo, aqui está process_word:
def process_word(self, word, order=2):
if len(self.prefix) < order:
self.prefix += (word)
return
try:
self.suffix_map[self.prefix].append(word)
except KeyError:
# se não houver entradas deste prefixo, crie uma.
self.suffix_map[self.prefix] = [word]
self.prefix = shift(self.prefix, word)
Transformar um programa como esse – alterando o projeto sem mudar o comportamento – é outro exemplo de refatoração (veja “Refatoração”, na página 70).
Este exemplo sugere um plano de desenvolvimento para projetar objetos e métodos:
-
Comece escrevendo funções que leiam e criem variáveis globais (quando necessário).
-
Uma vez que o programa esteja funcionando, procure associações entre variáveis globais e funções que as usem.
-
Encapsule variáveis relacionadas como atributos de objeto.
-
Transforme as funções associadas em métodos da nova classe.
Como exercício, baixe o meu código de Markov de http://thinkpython2.com/code/markov.py e siga os passos descritos acima para encapsular as variáveis globais como atributos de uma nova classe chamada Markov.
Solução: http://thinkpython2.com/code/Markov.py (observe o M maiúsculo).
18.10 - Depuração
A herança pode dificultar a depuração porque quando você invoca um método em um objeto, pode ser difícil compreender qual método será invocado.
Suponha que esteja escrevendo uma função que funcione com objetos Hand. Você gostaria que ela funcionasse com todos os tipos de Hand, como PokerHands, BridgeHands etc. Se invocar um método como shuffle, poderá receber o que foi definido em Deck, mas se alguma das subclasses ignorar este método, você receberá outra versão. Este comportamento pode ser bom, mas também confuso.
A qualquer momento em que não esteja seguro a respeito do fluxo de execução do seu programa, a solução mais simples é acrescentar instruções de exibição no início dos métodos em questão. Se Deck.shuffle exibir uma mensagem que diz algo como Running Deck.shuffle, então no decorrer da execução do programa ele monitora seu fluxo.
Uma alternativa é usar esta função, que recebe um objeto e um nome de método (como uma string) e retorna a classe que fornece a definição do método:
def find_defining_class(obj, meth_name):
for ty in type(obj).mro():
if meth_name in ty.__dict__:
return ty
Aqui está um exemplo:
>>> hand = Hand()
>>> find_defining_class(hand, 'shuffle')
<class 'Card.Deck'>
Então o método shuffle deste Hand é o de Deck.
find_defining_class usa o método mro para obter a lista de objetos de classe (tipos) onde os métodos serão procurados. “MRO” significa “ordem de resolução do método”, que é a sequência de classes que o Python pesquisa para “descobrir” um nome de método.
Aqui está uma sugestão de projeto: quando você ignora um método, a interface do novo método deve ser a mesma que a do antigo. Ela deve receber os mesmos parâmetros, retornar o mesmo tipo e obedecer às mesmas precondições e pós-condições. Se seguir esta regra, você descobrirá que qualquer função projetada para funcionar com uma instância de uma classe pai, como Deck, também funcionará com instâncias de classes filho como Hand e PokerHand.
Se violar esta regra, o que se chama de “princípio de substituição de Liskov”, seu código cairá como (desculpe) um castelo de cartas.
18.11 - Glossário
codificar
Representar um conjunto de valores usando outro conjunto de valores construindo um mapeamento entre eles.
atributo de classe
Atributo associado a um objeto de classe. Os atributos de classe são definidos dentro de uma definição de classe, mas fora de qualquer método.
atributo de instância
Atributo associado a uma instância de uma classe.
folheado
Método ou função que apresenta uma interface diferente para outra função sem fazer muitos cálculos.
herança
Capacidade de definir uma nova classe que seja uma versão modificada de uma classe definida anteriormente.
classe-pai
Classe da qual uma classe-filho herda.
classe-filho
Nova classe criada por herança de uma classe existente; também chamada de “subclasse”.
relação IS-A
Relação entre uma classe-filho e sua classe-pai. Também chamada de herança.
relação HAS-A
Relação entre duas classes onde as instâncias de uma classe contêm referências a instâncias da outra. Também chamada de composição.
dependência
Relação entre duas classes onde as instâncias de uma classe usam instâncias de outra classe, mas não as guardam como atributos.
diagrama de classe
Diagrama que mostra as classes em um programa e as relações entre elas.
multiplicidade
Notação em um diagrama de classe que mostra, para uma relação HAS-A, quantas referências a instâncias da outra classe podem existir.
encapsulamento de dados
Plano de desenvolvimento de programa que envolve um protótipo usando variáveis globais e uma versão final que transforma as variáveis globais em atributos de instância.
18.12 - Exercícios
Exercício 18.1
Para o seguinte programa, desenhe um diagrama de classe UML que mostre estas classes e as relações entre elas.
class PingPongParent:
pass
class Ping(PingPongParent):
def __init__(self, pong):
self.pong = pong
class Pong(PingPongParent):
def __init__(self, pings=None):
if pings is None:
self.pings = []
else:
self.pings = pings
def add_ping(self, ping):
self.pings.append(ping)
pong = Pong()
ping = Ping(pong)
pong.add_ping(ping)
Exercício 18.2
Escreva um método Deck chamado deal_hands que receba dois parâmetros: o número de mãos e o número de cartas por mão. Ele deve criar o número adequado de objetos Hand, lidar com o número adequado de cartas por mão e retornar uma lista de Hands.
Exercício 18.3
A seguir, as mãos possíveis no pôquer, em ordem crescente de valor e ordem decrescente de probabilidade:
par
Duas cartas com o mesmo valor.
dois pares
Dois pares de cartas com o mesmo valor.
trinca
Três cartas com o mesmo valor.
sequência
Cinco cartas com valores em sequência (os ases podem ser altos ou baixos, então Ace-2-3-4-5 é uma sequência, assim como 10-Jack-Queen-King-Ace, mas Queen-King-Ace-2-3 não é)
flush
Cinco cartas com o mesmo naipe.
full house
Três cartas com um valor, duas cartas com outro.
quadra
Quatro cartas com o mesmo valor.
straight flush
Cinco cartas em sequência (como definido acima) e com o mesmo naipe.
A meta desses exercícios é estimar a probabilidade de ter estas várias mãos.
- Baixe os seguintes arquivos de http://thinkpython2.com/code:
-
Card.py: Versão completa das classes Card, Deck e Hand deste capítulo. -
PokerHand.py: Uma implementação incompleta de uma classe que representa uma mão de pôquer e código para testá-la.
-
Se executar PokerHand.py, você verá que o programa cria mãos de pôquer com 7 cartas e verifica se alguma delas contém um flush. Leia este código com atenção antes de continuar.
-
Acrescente métodos a PokerHand.py chamados
has_pair,has_twopair, etc. que retornem True ou False conforme a mão cumpra os critérios em questão. Seu código deve funcionar corretamente para “mãos” que contenham qualquer número de cartas (embora 5 e 7 sejam as quantidades mais comuns). -
Escreva um método chamado classify que descubra a classificação do valor mais alto para uma mão e estabeleça o atributo label em questão. Por exemplo, uma mão de 7 cartas poderia conter um flush e um par; ela deve ser marcada como “flush”.
-
Quando se convencer de que os seus métodos de classificação estão funcionando, o próximo passo deve ser estimar as probabilidades de várias mãos. Escreva uma função em PokerHand.py que embaralhe cartas, divida-as em mãos, classifique as mãos e conte o número de vezes em que várias classificações aparecem.
-
Exiba uma tabela das classificações e suas probabilidades. Execute seu programa com números cada vez maiores de mãos até que os valores de saída convirjam a um grau razoável de exatidão. Compare seus resultados com os valores em http://en.wikipedia.org/wiki/Hand_rankings.
Solução: http://thinkpython2.com/code/PokerHandSoln.py.
Capítulo 19: Extra
Uma das minhas metas com este livro é ensinar o mínimo possível de Python. Quando havia duas formas de fazer algo, escolhia uma e evitava mencionar a outra. Ou, às vezes, usava a segunda como exercício.
Agora quero voltar a algumas coisas boas que ficaram para trás. O Python oferece vários recursos que não são realmente necessários – você pode escrever um bom código sem eles – mas com eles é possível escrever um código mais conciso, legível ou eficiente e, às vezes, todos os três.
19.1 - Expressões condicionais
Vimos instruções condicionais em “Execução condicional”, na página 78. As instruções condicionais muitas vezes são usadas para escolher um entre dois valores; por exemplo:
if x > 0:
y = math.log(x)
else:
y = float('nan')
Esta instrução verifica se x é positivo. Nesse caso, ela calcula math.log. Do contrário, math.log causaria um ValueError. Para evitar interromper o programa, geramos um “NaN”, que é um valor de ponto flutuante especial que representa um “Não número”.
Podemos escrever essa instrução de forma mais concisa usando uma expressão condicional:
y = math.log(x) if x > 0 else float('nan')
Você quase pode ler esta linha como se tivesse sido escrita em inglês: “y recebe log-x se x for maior que 0; do contrário, ele recebe NaN”.
As funções recursivas por vezes podem ser reescritas usando expressões condicionais. Por exemplo, aqui está uma versão recursiva de factorial:
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
Podemos reescrevê-la assim:
def factorial(n):
return 1 if n == 0 else n * factorial(n-1)
Outro uso de expressões condicionais é lidar com argumentos opcionais. Por exemplo, aqui está o método init de GoodKangaroo (veja o Exercício 17.2):
def __init__(self, name, contents=None):
self.name = name
if contents == None:
contents = []
self.pouch_contents = contents
Podemos reescrevê-lo assim:
def __init__(self, name, contents=None):
self.name = name
self.pouch_contents = [] if contents == None else contents
Em geral, é possível substituir uma instrução condicional por uma expressão condicional se ambos os ramos contiverem expressões simples que sejam retornadas ou atribuídas à mesma variável.
19.2 - Abrangência de listas
Em “Mapeamento, filtragem e redução”, na página 147, vimos os padrões de filtragem e mapeamento. Por exemplo, esta função toma uma lista de strings, mapeia o método de string capitalize aos elementos, e retorna uma nova lista de strings:
def capitalize_all(t):
res = []
for s in t:
res.append(s.capitalize())
return res
Podemos escrever isso de forma mais concisa usando abrangência de listas (list comprehension):
def capitalize_all(t):
return [s.capitalize() for s in t]
Os operadores de colchete indicam que estamos construindo uma nova lista. A expressão dentro dos colchetes especifica os elementos da lista, e a cláusula for indica qual sequência estamos atravessando.
A sintaxe da abrangência de listas é um pouco esquisita porque a variável de loop, s nesse exemplo, aparece na expressão antes de chegarmos à definição.
Abrangências de listas também podem ser usadas para filtragem. Por exemplo, esta função só seleciona os elementos de t que são maiúsculos, e retorna uma nova lista:
def only_upper(t):
res = []
for s in t:
if s.isupper():
res.append(s)
return res
Podemos reescrevê-la usando abrangência de listas:
def only_upper(t):
return [s for s in t if s.isupper()]
Abrangências de listas são concisas e fáceis de ler, pelo menos para expressões simples. E são normalmente mais rápidas que os loops for equivalentes, às vezes muito mais rápidas. Então, se você ficar irritado comigo por não ter mencionado isso antes, eu entendo.
Porém, em minha defesa, as abrangências de listas são mais difíceis de depurar porque não é possível ter instruções de exibição dentro do loop. Sugiro que você as use só se o cálculo for simples o suficiente para que acerte já de primeira. E para principiantes isso significa nunca.
19.3 - Expressões geradoras
Expressões geradoras são semelhantes às abrangências de listas, mas com parênteses em vez de colchetes:
>>> g = (x**2 for x in range(5))
>>> g
<generator object <genexpr> at 0x7f4c45a786c0>
O resultado é um objeto gerador que sabe como fazer iterações por uma sequência de valores. No entanto, ao contrário de uma abrangência de listas, ele não calcula todos os valores de uma vez; espera pelo pedido. A função integrada next recebe o próximo valor do gerador:
>>> next(g)
0
>>> next(g)
1
Quando você chega no fim da sequência, next cria uma exceção StopIteration. Também é possível usar um loop for para fazer a iteração pelos valores:
>>> for val in g:
... print(val)
4
9
16
O objeto gerador monitora a posição em que está na sequência, portanto o loop for continua de onde next parou. Uma vez que o gerador se esgotar, ele continua criando StopException:
>>> next(g)
StopIteration
As expressões geradoras muitas vezes são usadas com funções como sum, max e min:
>>> sum(x**2 for x in range(5))
30
19.4 - any e all
O Python tem uma função integrada, any, que recebe uma sequência de valores booleanos e retorna True se algum dos valores for True. Ela funciona em listas:
>>> any([False, False, True])
True
Entretanto, muitas vezes é usada com expressões geradoras:
>>> any(letter == 't' for letter in 'monty')
True
Esse exemplo não é muito útil porque faz a mesma coisa que o operador in. Porém, podemos usar any para reescrever algumas das funções de pesquisa que escrevemos em “Busca”, na página 136. Por exemplo, poderíamos escrever avoids dessa forma:
def avoids(word, forbidden):
return not any(letter in forbidden for letter in word)
A função quase pode ser lida como uma frase em inglês: “word evita forbidden se não houver nenhuma letra proibida em word”.
Usar any com uma expressão geradora é eficiente porque ela retorna imediatamente se encontrar um valor True, então não é preciso avaliar a sequência inteira.
O Python oferece outra função integrada, all, que retorna True se todos os elementos da sequência forem True. Como exercício, use all para reescrever uses_all de “Busca”, na página 136.
19.5 - Conjuntos
Na seção “Subtração de dicionário”, da página 198, uso dicionários para encontrar as palavras que aparecem em um documento, mas não numa lista de palavras. A função que escrevi recebe d1, que contém as palavras do documento como chaves e d2, que contém a lista de palavras. Ela retorna um dicionário que contém as chaves de d1 que não estão em d2:
def subtract(d1, d2):
res = dict()
for key in d1:
if key not in d2:
res[key] = None
return res
Em todos esses dicionários, os valores não são None porque nunca os usamos. O resultado é que desperdiçamos espaço de armazenamento.
O Python fornece outro tipo integrado, chamado set (conjunto), que se comporta como uma coleção de chaves de dicionário sem valores. Acrescentar elementos a um conjunto é rápido; assim como verificar a adesão. E os conjuntos fornecem métodos e operadores para calcular operações de conjuntos.
Por exemplo, a subtração de conjuntos está disponível como um método chamado difference ou como um operador, -. Portanto, podemos reescrever subtract desta forma:
def subtract(d1, d2):
return set(d1) - set(d2)
O resultado é um conjunto em vez de um dicionário, mas, para operações como iteração, o comportamento é o mesmo.
Alguns exercícios neste livro podem ser feitos de forma concisa e eficiente com conjuntos. Por exemplo, aqui está uma solução para has_duplicates, do Exercício 10.7, que usa um dicionário:
def has_duplicates(t):
d = {}
for x in t:
if x in d:
return True
d[x] = True
return False
Quando um elemento aparece pela primeira vez, ele é acrescentado ao dicionário. Se o mesmo elemento aparece novamente, a função retorna True.
Usando conjuntos, podemos escrever a mesma função dessa forma:
def has_duplicates(t):
return len(set(t)) < len(t)
Um elemento só pode aparecer em um conjunto uma vez, portanto, se um elemento em t aparecer mais de uma vez, o conjunto será menor que t. Se não houver duplicatas, o conjunto terá o mesmo tamanho que t.
Também podemos usar conjuntos para fazer alguns exercícios no Capítulo 9. Por exemplo, aqui está uma versão de uses_only com um loop:
def uses_only(word, available):
for letter in word:
if letter not in available:
return False
return True
uses_only verifica se todas as cartas em word estão em available. Podemos reescrevê-la assim:
def uses_only(word, available):
return set(word) <= set(available)
O operador <= verifica se um conjunto é um subconjunto ou outro, incluindo a possibilidade de que sejam iguais, o que é verdade se todas as letras de word aparecerem em available.
Como exercício, reescreva avoids usando conjuntos.
19.6 - Contadores
Um contador é como um conjunto, exceto que se um elemento aparecer mais de uma vez, o contador registra quantas vezes ele aparece. Se tiver familiaridade com a ideia matemática de um multiconjunto (multiset), um contador é uma forma natural de representar um multiconjunto.
Contadores são definidos em um módulo padrão chamado collections, portanto é preciso importá-lo. Você pode inicializar um contador com uma string, lista ou alguma outra coisa que seja compatível com iteração:
>>> from collections import Counter
>>> count = Counter('parrot')
>>> count
Counter({'r': 2, 't': 1, 'o': 1, 'p': 1, 'a': 1})
Os contadores comportam-se como dicionários de muitas formas; eles mapeiam cada chave ao número de vezes que aparece. Como em dicionários, as chaves têm de ser hashable.
Ao contrário de dicionários, os contadores não causam uma exceção se você acessar um elemento que não aparece. Em vez disso, retornam 0:
>>> count['d']
0
Podemos usar contadores para reescrever is_anagram do Exercício 10.6:
def is_anagram(word1, word2):
return Counter(word1) == Counter(word2)
Se duas palavras forem anagramas, elas contêm as mesmas letras com as mesmas contagens, então seus contadores são equivalentes.
Os contadores oferecem métodos e operadores para executar operações similares às dos conjuntos, incluindo adição, subtração, união e intersecção. E eles fornecem um método muitas vezes útil, most_common, que retorna uma lista de pares frequência-valor, organizados do mais ao menos comum:
>>> count = Counter('parrot')
>>> for val, freq in count.most_common(3):
... print(val, freq)
r 2
p 1
a 1
19.7 - defaultdict
O módulo collections também tem defaultdict, que se parece com um dicionário, exceto pelo fato de que se você acessar uma chave que não existe, um novo valor pode ser gerado automaticamente.
Quando você cria um defaultdict, fornece uma função usada para criar valores. Uma função usada para criar objetos às vezes é chamada de factory (fábrica). As funções integradas que criam listas, conjuntos e outros tipos podem ser usadas como fábricas:
>>> from collections import defaultdict
>>> d = defaultdict(list)
Note que o argumento é list, que é um objeto de classe, não list(), que é uma nova lista. A função que você fornece não é chamada a menos que você acesse uma chave que não existe:
>>> t = d['new key']
>>> t
[]
A nova lista, que estamos chamando de t, também é adicionada ao dicionário. Então, se alterarmos t, a mudança aparece em d:
>>> t.append('new value')
>>> d
defaultdict(<class 'list'>, {'new key': ['new value']})
Se estiver fazendo um dicionário de listas, você pode escrever um código mais simples usando defaultdict. Na minha solução para o Exercício 12.2, que você pode ver em http://thinkpython2.com/code/anagram_sets.py, faço um dicionário que mapeia uma string organizada de letras a uma lista de palavras que pode ser soletrada com essas letras. Por exemplo, 'opst' mapeia para a lista ['opts', 'post', 'pots', 'spot', 'stop', 'tops'].
Aqui está o código original:
def all_anagrams(filename):
d = {}
for line in open(filename):
word = line.strip().lower()
t = signature(word)
if t not in d:
d[t] = [word]
else:
d[t].append(word)
return d
Isso pode ser simplificado usando setdefault, que você poderia ter usado no Exercício 11.2:
def all_anagrams(filename):
d = {}
for line in open(filename):
word = line.strip().lower()
t = signature(word)
d.setdefault(t, []).append(word)
return d
O problema dessa solução é que ela faz uma lista nova a cada vez, mesmo que não seja necessário. Para listas, isso não é grande coisa, mas se a função fábrica for complicada, poderia ser.
Podemos evitar este problema e simplificar o código usando um defaultdict:
def all_anagrams(filename):
d = defaultdict(list)
for line in open(filename):
word = line.strip().lower()
t = signature(word)
d[t].append(word)
return d
A minha solução para o Exercício 18.3, que você pode baixar em http://thinkpython2.com/code/PokerHandSoln.py, usa setdefault na função has_straightflush. O problema dessa solução é criar um objeto Hand cada vez que passa pelo loop, seja ele necessário ou não. Como exercício, reescreva-a usando um defaultdict.
19.8 - Tuplas nomeadas
Muitos objetos simples são basicamente coleções de valores relacionados. Por exemplo, o objeto Point, definido no Capítulo 15, contém dois números, x e y. Ao definir uma classe como essa, normalmente você começa com um método init e um método str:
class Point:
def __init__(self, x=0, y=0):
self.x = x
self.y = y
def __str__(self):
return '(%g, %g)' % (self.x, self.y)
É muito código para transmitir pouca informação. O Python tem uma forma mais concisa de dizer a mesma coisa:
from collections import namedtuple
Point = namedtuple('Point', ['x', 'y'])
O primeiro argumento é o nome da classe que você quer criar. O segundo é uma lista dos atributos que o objeto Point deve ter, como strings. O valor de retorno de namedtuple é um objeto de classe:
>>> Point
<class '__main__.Point'>
Point fornece automaticamente métodos como __init__ e __str__ então não é preciso escrevê-los.
Para criar um objeto Point, você usa a classe Point como uma função:
>>> p = Point(1, 2)
>>> p
Point(x=1, y=2)
O método __init__ atribui os argumentos a atributos usando os nomes que você forneceu. O método __str__ exibe uma representação do objeto Point e seus atributos.
Você pode acessar os elementos da tupla nomeada pelo nome:
>>> p.x, p.y
(1, 2)
Mas também pode tratar uma tupla nomeada como uma tupla:
>>> p[0], p[1]
(1, 2)
>>> x, y = p
>>> x, y
(1, 2)
Tuplas nomeadas fornecem uma forma rápida de definir classes simples. O problema é que classes simples não ficam sempre simples. Mais adiante você poderá decidir que quer acrescentar métodos a uma tupla nomeada. Nesse caso, você poderá definir uma nova classe que herde da tupla nomeada:
class Pointier(Point):
# adicionar mais métodos aqui
Ou poderá mudar para uma definição de classe convencional.
19.9 - Reunindo argumentos de palavra-chave
Em “Tuplas com argumentos de comprimento variável”, na página 181, vimos como escrever uma função que reúne seus argumentos em uma tupla:
def printall(*args):
print(args)
Você pode chamar esta função com qualquer número de argumentos posicionais (isto é, argumentos que não têm palavras-chave):
>>> printall(1, 2.0, '3')
(1, 2.0, '3')
Porém, o operador * não reúne argumentos de palavra-chave:
>>> printall(1, 2.0, third='3')
TypeError: printall() got an unexpected keyword argument 'third'
Para reunir argumentos de palavra-chave, você pode usar o operador **:
def printall(*args, **kwargs):
print(args, kwargs)
Você pode chamar o parâmetro de coleta de palavra-chave, como quiser, mas kwargs é uma escolha comum. O resultado é um dicionário que mapeia palavras-chave a valores:
>>> printall(1, 2.0, third='3')
(1, 2.0) {'third': '3'}
Se tiver um dicionário de palavras-chave e valores, pode usar o operador de dispersão, **, para chamar uma função:
>>> d = dict(x=1, y=2)
>>> Point(**d)
Point(x=1, y=2)
Sem o operador de dispersão, a função trataria d como um único argumento posicional, e então atribuiria d a x e se queixaria porque não há nada para atribuir a y:
>>> d = dict(x=1, y=2)
>>> Point(d)
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
TypeError: __new__() missing 1 required positional argument: 'y'
Quando estiver trabalhando com funções com um grande número de parâmetros, muitas vezes é útil criar dicionários e passá-los como argumentos para especificar as opções usadas com maior frequência.
19.10 - Glossário
expressão condicional
Expressão que contém um de dois valores, dependendo de uma condição.
abrangência de lista (list comprehension)
Expressão com um loop for entre colchetes que produz uma nova lista.
expressão geradora
Uma expressão com um loop for entre parênteses que produz um objeto gerador.
multiconjunto
Entidade matemática que representa um mapeamento entre os elementos de um conjunto e o número de vezes que aparecem.
fábrica (factory)
Função normalmente passada como parâmetro, usada para criar objetos.
19.11 - Exercícios
Exercício 19.1
Esta é uma função que calcula o coeficiente binominal recursivamente:
def binomial_coeff(n, k):
"""Compute the binomial coefficient "n choose k".
n: number of trials
k: number of successes
returns: int
"""
if k == 0:
return 1
if n == 0:
return 0
res = binomial_coeff(n-1, k) + binomial_coeff(n-1, k-1)
return res
Reescreva o corpo da função usando expressões condicionais aninhadas.
Uma observação: esta função não é muito eficiente porque acaba calculando os mesmos valores várias vezes. Você pode torná-lo mais eficiente com memos (veja “Memos”, na página 169). No entanto, vai ver que é mais difícil usar memos se escrevê-la usando expressões condicionais.
Apêndice A: Depuração
Durante a depuração, você deve distinguir entre tipos diferentes de erros para rastreá-los mais rapidamente:
-
Erros de sintaxe são descobertos pelo interpretador quando ele está traduzindo o código-fonte para código de bytes. Eles indicam que há algo errado com a estrutura do programa. Exemplo: a omissão dos dois pontos no fim de uma instrução def gera a mensagem um tanto redundante SyntaxError: invalid syntax.
-
Erros de tempo de execução são produzidos pelo interpretador se algo der errado durante a execução do programa. A maior parte das mensagens de erro de tempo de execução inclui informações sobre onde o erro ocorreu e o que as funções estavam fazendo. Exemplo: a recursividade infinita eventualmente leva ao erro de tempo de execução maximum recursion depth exceeded.
-
Erros semânticos são problemas com um programa que é executado sem produzir mensagens de erro, mas que não faz a coisa certa. Exemplo: uma expressão que não pode ser avaliada na ordem esperada, produzindo um resultado incorreto.
O primeiro passo da depuração é compreender com que tipo de erro você está lidando. Embora as próximas seções sejam organizadas pelo tipo de erro, algumas técnicas são aplicáveis em mais de uma situação.
A.1 - Erros de sintaxe
Os erros de sintaxe normalmente são fáceis de corrigir, uma vez que você descubra quais são. Infelizmente, as mensagens de erro muitas vezes não são úteis. As mensagens mais comuns são SyntaxError: invalid syntax e SyntaxError: invalid token, e nenhuma das duas é muito informativa.
Por outro lado, a mensagem diz onde no programa o problema ocorreu. E, na verdade, diz a você onde o Python notou um problema, que é não necessariamente onde o erro está. Às vezes, o erro está antes da posição da mensagem de erro, muitas vezes na linha precedente.
Se estiver construindo o programa incrementalmente, você terá uma boa ideia sobre onde encontrar o erro. Estará na última linha que acrescentou.
Se estiver copiando o código de um livro, comece comparando com atenção o seu código e o do livro. Verifique cada caractere. Ao mesmo tempo, lembre-se de que o livro pode estar errado, então, se vir algo que parece um erro de sintaxe, pode ser mesmo.
Aqui estão algumas formas de evitar os erros de sintaxe mais comuns:
-
Confira se não está usando uma palavra-chave do Python para um nome de variável.
-
Verifique se há dois pontos no fim do cabeçalho de cada instrução composta, incluindo instruções for, while, if e def.
-
Confira se as strings no código têm as aspas correspondentes. Verifique se todas as aspas são retas, em vez de curvas.
-
Se tiver strings com várias linhas com aspas triplas (simples ou duplas), confira se fechou a string adequadamente. Uma string não fechada pode causar um erro de invalid token no fim do seu programa, ou pode tratar a parte seguinte do programa como uma string até chegar à string seguinte. No segundo caso, o programa pode nem produzir uma mensagem de erro!
-
Um operador inicial aberto –
(,{ou[– faz o Python continuar até a linha seguinte, como se esta fosse parte da instrução atual. Geralmente, um erro ocorre quase imediatamente na linha seguinte. -
Confira se há o clássico
=em vez do==dentro de uma condicional. -
Verifique a endentação para ter certeza de que está alinhada como deveria. O Python pode lidar com espaços e tabulações, mas, se misturá-los, isso pode causar problemas. A melhor forma de evitar esse problema é usar um editor de texto que identifique o Python e gere endentação consistente.
-
Se há caracteres não ASCII no código (incluindo strings e comentários), isso pode causar problemas, embora o Python 3 normalmente lide com caracteres não ASCII. Tenha cuidado se colar texto de uma página web ou outra fonte.
Se nada funcionar, vá para a próxima seção...
A.1.1 - Continuo fazendo alterações e não faz nenhuma diferença
Se o interpretador disser que há um erro e você não o encontra, pode ser que você e o interpretador não estejam olhando para o mesmo código. Verifique o seu ambiente de programação para ter certeza de que o programa que está editando é o mesmo que o Python está tentando executar.
Se não estiver certo, tente pôr um erro de sintaxe óbvio e deliberado no início do programa. Agora execute-o novamente. Se o interpretador não encontrar o novo erro, você não está executando o novo código.
Há alguns culpados prováveis:
-
Você editou o arquivo e esqueceu de salvar as alterações antes de executá-lo novamente. Alguns ambientes de programação fazem isso para você, mas alguns não fazem.
-
Você mudou o nome do arquivo, mas ainda está executando o nome antigo.
-
Algo no seu ambiente de desenvolvimento está configurado incorretamente.
-
Se estiver escrevendo um módulo e usando import, confira se não usou o mesmo nome no seu módulo que os dos módulos padrão do Python.
-
Se você estiver usando import para ler um módulo, lembre-se de que é preciso reiniciar o interpretador ou usar reload para ler um arquivo alterado. Se importar o módulo novamente, ele não faz nada.
Se já esgotou as possibilidades e não conseguiu descobrir o que está acontecendo, uma abordagem é começar novamente com um programa como “Hello, World!”, para ter certeza de que consegue executar um programa conhecido. Então, gradualmente acrescente as partes do programa original ao novo.
A.2 - Erros de tempo de execução
Uma vez que o seu programa esteja sintaticamente correto, o Python pode lê-lo e, pelo menos, começar a executá-lo. O que poderia dar errado?
A.2.1 - Meu programa não faz nada
Este problema é mais comum quando o seu arquivo é composto de funções e classes, mas na verdade não invoca uma função para começar a execução. Isso pode ser intencional se você só planeja importar este módulo para fornecer classes e funções.
Se não for intencional, tenha certeza de que há uma chamada de função no programa, e que o fluxo de execução o alcança (veja “Fluxo da execução” a seguir).
A.2.2 - Meu programa trava
Se um programa parar e parecer que não está fazendo nada, ele está “travado”. Muitas vezes isso significa que está preso em um loop ou recursão infinita.
-
Se houver determinado loop que você suspeita ser o problema, acrescente uma instrução print imediatamente antes do loop que diga “entrando no loop”, e outra imediatamente depois que diga “saindo do loop”.
Execute o programa. Se receber a primeira mensagem e a segunda não, você tem um loop infinito. Vá à seção “Loop infinito” mais adiante. -
Na maior parte do tempo, a recursividade infinita fará com que o programa seja executado durante algum tempo e então gere um erro “RuntimeError: Maximum recursion depth exceeded”. Se isso acontecer, vá à seção “Recursividade infinita” mais adiante.
Se não estiver recebendo este erro, mas suspeita que há um problema com um método ou função recursiva, você ainda pode usar as técnicas da seção “Recursividade infinita”. -
Se nenhum desses passos funcionar, comece a testar outros loops e outras funções e métodos recursivos.
-
Se isso não funcionar, então é possível que você não entenda o fluxo de execução do seu programa. Vá à seção “Fluxo de execução” mais adiante.
Loop infinito
Se você acha que há um loop infinito e talvez saiba qual loop está causando o problema, acrescente uma instrução print no fim do loop que exiba os valores das variáveis na condição e o valor da condição.
Por exemplo:
while x > 0 and y < 0 :
# faz algo com x
# faz algo com y
print('x: ', x)
print('y: ', y)
print("condition: ", (x > 0 and y < 0))
Agora, quando executar o programa, você verá três linhas de saída para cada vez que o programa passar pelo loop. Na última vez que passar pelo loop, a condição deve ser False. Se o loop continuar, você poderá ver os valores de x e y, e compreender porque não estão sendo atualizados corretamente.
Recursividade infinita
Na maioria das vezes, a recursividade infinita faz o programa rodar durante algum tempo e então produzir um erro de "Maximum recursion depth exceeded".
Se suspeitar que uma função está causando recursividade infinita, confira se há um caso-base. Deve haver alguma condição que faz a função retornar sem fazer uma invocação recursiva. Do contrário, você terá que repensar o algoritmo e identificar um caso-base.
Se houver um caso-base, mas o programa não parece alcançá-lo, acrescente uma instrução print no início da função para exibir os parâmetros. Agora, quando executar o programa, você verá algumas linhas de saída cada vez que a função for invocada, e verá os valores dos parâmetros. Se os parâmetros não estiverem se movendo em direção ao caso-base, você terá algumas ideias sobre a razão disso.
Fluxo de execução
Se não tiver certeza de como o fluxo de execução está se movendo pelo seu programa, acrescente instruções print ao começo de cada função com uma mensagem como “entrada na função foo”, onde foo é o nome da função.
Agora, quando executar o programa, ele exibirá cada função que for invocada.
A.2.3 - Quando executo o programa recebo uma exceção
Se algo der errado durante o tempo de execução, o Python exibe uma mensagem que inclui o nome da exceção, a linha do programa onde o problema ocorreu, e um traceback.
O traceback identifica a função que está rodando atualmente, e a função que a chamou, assim como a função que chamou esta, e assim por diante. Em outras palavras, ele traça a sequência de chamadas de função que fez com que você chegasse onde está, incluindo o número da linha no seu arquivo onde cada chamada ocorreu.
O primeiro passo é examinar o lugar no programa onde o erro ocorreu e ver se consegue compreender o que aconteceu. Esses são alguns dos erros de tempo de execução mais comuns:
NameError
Você está tentando usar uma variável que não existe no ambiente atual. Confira se o nome está escrito corretamente e de forma consistente. E lembre-se de que as variáveis locais são locais; você não pode se referir a elas a partir do exterior da função onde são definidas.
TypeError
Há várias causas possíveis:
-
Você está tentando usar um valor de forma inadequada. Exemplo: indexar uma string, lista ou tupla com algo diferente de um número inteiro.
-
Não há correspondência entre os itens em uma string de formatação e os itens passados para conversão. Isso pode acontecer se o número de itens não tiver correspondência ou uma conversão inválida for chamada.
-
Você está passando o número incorreto de argumentos a uma função. Para métodos, olhe para a definição do método e verifique se o primeiro parâmetro é self. Então olhe para a invocação do método; confira se está invocando o método a um objeto com o tipo correto e fornecendo os outros argumentos corretamente.
KeyError
Você está tentando acessar um elemento de um dicionário usando uma chave que o dicionário não contém. Se as chaves forem strings, lembre-se de que letras maiúsculas são diferentes de minúsculas.
AttributeError
Você está tentando acessar um atributo ou método que não existe. Verifique a ortografia! Você pode usar a função integrada vars para listar os atributos que existem mesmo.
Se um AttributeError indicar que um objeto é do tipo NoneType, fica subentendido que é None. Então o problema não é o nome do atributo, mas o objeto.
Pode ser que o objeto seja none porque você se esqueceu de retornar um valor de uma função; se chegar ao fim de uma função sem chegar a uma instrução return, ela retorna None. Outra causa comum é usar o resultado de um método de lista, como sort, que retorne None.
IndexError
O índice que você está usando para acessar uma lista, string ou tupla é maior que o seu comprimento menos um. Imediatamente antes do local do erro, acrescente uma instrução print para exibir o valor do índice e o comprimento do array. O array é do tamanho certo? O índice tem o valor certo?
O depurador do Python (pdb) é útil para rastrear exceções porque permite examinar o estado do programa imediatamente antes do erro. Você pode ler sobre o pdb em https://docs.python.org/3/library/pdb.html.
A.2.4 - Acrescentei tantas instruções print que fui inundado pelos resultados
Um dos problemas com a utilização de instruções print para a depuração é que você pode terminar enterrado pelos resultados. Há duas formas de prosseguir: simplifique a saída ou simplifique o programa.
Para simplificar a saída, você pode retirar ou transformar as instruções print que não estão ajudando em comentários, ou combiná-las, ou formatar a saída para que seja mais fácil de entender.
Para simplificar o programa, há várias coisas que você pode fazer. Em primeiro lugar, reduza o problema no qual o programa está trabalhando. Por exemplo, se está fazendo uma busca em uma lista, procure em uma lista pequena. Se o programa receber entradas do usuário, dê a entrada mais simples possível que cause o problema.
Em segundo lugar, limpe o programa. Retire o código morto e reorganize o programa para torná-lo o mais fácil possível de ler. Por exemplo, se você suspeitar que o problema está em uma parte profundamente aninhada do programa, tente reescrever aquela parte com uma estrutura mais simples. Se suspeitar de uma função grande, tente quebrá-la em funções menores para testá-las separadamente.
Muitas vezes, o próprio processo de encontrar o caso de teste mínimo leva você ao problema. Se descobrir que um programa funciona em uma situação, mas não em outra, isso dá uma pista sobre o que está acontecendo.
De forma similar, reescrever uma parte do código pode ajudar a encontrar erros sutis. Se fizer uma alteração que você ache que não vai afetar o programa, mas que acabe afetando, isso pode ajudá-lo.
A.3 - Erros semânticos
De algumas formas, os erros semânticos são os mais difíceis de depurar, porque o interpretador não fornece nenhuma informação sobre qual é o problema. Só você sabe o que o programa deve fazer.
O primeiro passo é fazer uma conexão entre o texto do programa e o comportamento que está vendo. Você precisa de uma hipótese sobre o que o programa está fazendo de fato. Uma das coisas que torna isso difícil é que os computadores são rápidos.
Pode ser que você queira diminuir a velocidade do programa para ser equivalente à humana; com alguns depuradores é possível fazer isso. No entanto, o tempo que leva para inserir instruções print bem colocadas muitas vezes é curto em comparação ao da configuração do depurador, inserção e remoção de marcações e colocação do “compasso” do programa onde o erro está ocorrendo.
A.3.1 - Meu programa não funciona
Você deve se perguntar o seguinte:
-
Há algo que o programa deveria fazer, mas que não parece acontecer? Encontre a seção do código que executa a função em questão e confira se está sendo executada quando você acha que deveria.
-
Algo está acontecendo, mas não o que deveria? Encontre o código no seu programa que executa a função em questão e veja se está sendo executada na hora errada.
-
Uma seção do código está produzindo um efeito que não é o esperado? Tenha certeza de que entende o código em questão, especialmente se envolver funções ou métodos de outros módulos do Python. Leia a documentação das funções que chama. Teste-as escrevendo casos de teste simples e verificando os resultados.
Para programar, é preciso ter um modelo mental de como os programas funcionam. Se escrever um programa que não faz o que espera, muitas vezes o problema não está no programa, está no seu modelo mental.
A melhor forma de corrigir o seu modelo mental é quebrar o programa nos seus componentes (normalmente as funções e métodos) e testar cada componente em separado. Uma vez que encontre a discrepância entre o seu modelo e a realidade, poderá resolver o problema.
Naturalmente, você deveria construir e testar componentes conforme desenvolva o programa. Assim, se encontrar um problema, deve haver só uma pequena quantidade de código novo que não sabe se está correto.
A.3.2 - Tenho uma baita expressão cabeluda e ela não faz o que espero
Escrever expressões complexas é ótimo enquanto são legíveis, mas elas podem ser difíceis de depurar. Muitas vezes é uma boa ideia quebrar uma expressão complexa em uma série de atribuições a variáveis temporárias.
Por exemplo:
self.hands[i].addCard(self.hands[self.findNeighbor(i)].popCard())
A expressão pode ser reescrita assim:
neighbor = self.findNeighbor(i)
pickedCard = self.hands[neighbor].popCard()
self.hands[i].addCard(pickedCard)
A versão explícita é mais fácil de ler porque os nomes das variáveis oferecem documentação adicional, e é mais fácil de depurar porque você pode verificar os tipos das variáveis intermediárias e exibir seus valores.
Outro problema que pode ocorrer com grandes expressões é que a ordem da avaliação pode não ser o que você espera. Por exemplo, se estiver traduzindo a expressão 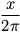 . para o Python, poderia escrever:
. para o Python, poderia escrever:
y = x / 2 * math.pi
Isso não está correto porque a multiplicação e a divisão têm a mesma precedência e são avaliadas da esquerda para a direita. Então, é assim que essa expressão é calculada: xπ/2.
Uma boa forma de depurar expressões é acrescentar parênteses para tornar a ordem da avaliação explícita:
y = x / (2 * math.pi)
Sempre que não tiver certeza sobre a ordem da avaliação, use parênteses. Além de o programa ficar correto (quanto à execução do que era pretendido), ele também será mais legível para outras pessoas que não memorizaram a ordem de operações.
A.3.3 - Tenho uma função que não retorna o que espero
Se tiver uma instrução return com uma expressão complexa, não há possibilidade de exibir o resultado antes do retorno. Novamente, você pode usar uma variável temporária. Por exemplo, em vez de:
return self.hands[i].removeMatches()
você poderia escrever:
count = self.hands[i].removeMatches()
return count
Agora você tem a oportunidade de exibir o valor de count antes do retorno.
A.3.4 - Estou perdido e preciso de ajuda
Em primeiro lugar, afaste-se do computador por alguns minutos. Computadores emitem ondas que afetam o cérebro, causando estes sintomas:
-
frustração e raiva;
-
crenças supersticiosas (“o computador me odeia”) e pensamento mágico (“o programa só funciona quando uso o meu chapéu virado para trás”);
-
programação aleatória (a tentativa de programar escrevendo todos os programas possíveis e escolhendo aquele que faz a coisa certa).
Se estiver sofrendo algum desses sintomas, levante-se e dê uma volta. Quando se acalmar, pense no programa. O que ele está fazendo? Quais são algumas causas possíveis para esse comportamento? Quando foi a última vez que tinha um programa funcionando, e o que fez depois disso?
Às vezes leva tempo para encontrar um erro. Com frequência encontro erros quando estou longe do computador e deixo a minha mente vagar. Os melhores lugares para encontrar erros são os trens, o chuveiro e a cama, logo antes de adormecer.
A.3.5 - Sério, preciso mesmo de ajuda
Acontece. Mesmo os melhores programadores ocasionalmente empacam. Pode ocorrer de você trabalhar tanto em um programa que não consegue enxergar o erro. Precisa de outro par de olhos.
Antes de trazer mais alguém, não se esqueça de se preparar. Seu programa deve ser o mais simples possível, e deve estar funcionando com a menor entrada possível que cause o erro. Deve ter instruções print nos lugares adequados (e a saída que produzem deve ser compreensível). Você deve entender o problema o suficiente para descrevê-lo de forma concisa.
Ao trazer alguém para ajudar, lembre-se de dar as informações de que a pessoa possa precisar:
-
Se houver uma mensagem de erro, qual é e que parte do programa indica?
-
Qual foi a última coisa que fez antes de este erro ocorrer? Quais foram as últimas linhas de código que escreveu, ou qual é o novo caso de teste que falhou?
-
O que tentou até agora e o que aprendeu?
Quando encontrar o erro, pense por um segundo no que poderia ter feito para encontrá-lo mais rápido. Na próxima vez em que vir algo similar, poderá encontrar o erro mais rapidamente.
Lembre-se, a meta não é só fazer o programa funcionar. A meta é aprender como fazer o programa funcionar.
Apêndice B: Análise de algoritmos
Este apêndice é um excerto editado de Think Complexity, por Allen B. Downey, também publicado pela O’Reilly Media (2012). Depois de ler este livro aqui, pode ser uma boa ideia lê-lo também.
Análise de algoritmos é um ramo da Ciência da Computação que estuda o desempenho de algoritmos, especialmente suas exigências de tempo de execução e requisitos de espaço. Veja http://en.wikipedia.org/wiki/Analysis_of_algorithms.
A meta prática da análise de algoritmos é prever o desempenho de algoritmos diferentes para guiar decisões de projeto.
Durante a campanha presidencial dos Estados Unidos de 2008, pediram ao candidato Barack Obama para fazer uma entrevista de emprego improvisada quando visitou a Google. O diretor executivo, Eric Schmidt, brincou, pedindo a ele “a forma mais eficiente de classificar um milhão de números inteiros de 32 bits”. Aparentemente, Obama tinha sido alertado porque respondeu na hora: “Creio que a ordenação por bolha (bubble sort) não seria a escolha certa”. Veja http://bit.ly/1MpIwTf.
Isso é verdade: a ordenação por bolha é conceitualmente simples, mas lenta para grandes conjuntos de dados. A resposta que Schmidt procurava provavelmente é “ordenação radix” (radix sort)[2].
A meta da análise de algoritmos é fazer comparações significativas entre algoritmos, mas há alguns problemas:
-
O desempenho relativo dos algoritmos pode depender de características do hardware; então um algoritmo pode ser mais rápido na Máquina A, e outro na Máquina B. A solução geral para este problema é especificar um modelo de máquina e analisar o número de passos ou operações que um algoritmo exige sob um modelo dado.
-
O desempenho relativo pode depender dos detalhes do conjunto de dados. Por exemplo, alguns algoritmos de ordenação rodam mais rápido se os dados já foram parcialmente ordenados; outros algoritmos rodam mais devagar neste caso. Uma forma comum de evitar este problema é analisar o pior caso. Às vezes é útil analisar o desempenho de casos médios, mas isso é normalmente mais difícil, e pode não ser óbvio qual conjunto de casos deve ser usado para a média.
-
O desempenho relativo também depende do tamanho do problema. Um algoritmo de ordenação que é rápido para pequenas listas pode ser lento para longas listas. A solução habitual para este problema é expressar o tempo de execução (ou o número de operações) como uma função do tamanho de problema e funções de grupo em categorias que dependem de sua velocidade de crescimento quando o tamanho de problema aumenta.
Uma coisa boa sobre este tipo de comparação é que ela é própria para a classificação simples de algoritmos. Por exemplo, se souber que o tempo de execução do algoritmo A tende a ser proporcional ao tamanho da entrada n, e o algoritmo B tende a ser proporcional a \( n^2 \), então espero que A seja mais rápido que B, pelo menos para valores grandes de n.
Esse tipo de análise tem algumas desvantagens, mas falaremos disso mais adiante.
B.1 - Ordem de crescimento
Vamos supor que você analisou dois algoritmos e expressou seus tempos de execução em relação ao tamanho da entrada: o algoritmo A leva 100n+1 passos para resolver um problema com o tamanho n; o algoritmo B leva \( n^2 + n + 1 \) passos.
A tabela seguinte mostra o tempo de execução desses algoritmos para tamanhos de problema diferentes:
| Tamanho da entrada | Tempo de execução do algoritmo A | Tempo de execução do algoritmo B |
| 10 | 1 001 | 111 |
| 100 | 10 001 | 10 101 |
| 1 000 | 100 001 | 1 001 001 |
| 10 000 | 1 000 001 | > 1010 |
Ao chegar em n=10, o algoritmo A parece bem ruim; ele é quase dez vezes mais longo que o algoritmo B. No entanto, para n=100 eles são bem parecidos, e, para valores maiores, A é muito melhor.
A razão fundamental é que para grandes valores de n, qualquer função que contenha um termo \( n^2 \) será mais rápida que uma função cujo termo principal seja n. O termo principal é o que tem o expoente mais alto.
Para o algoritmo A, o termo principal tem um grande coeficiente, 100, que é a razão de B ser melhor que A para um valor pequeno de n. Entretanto, apesar dos coeficientes, sempre haverá algum valor de n em que \( an^2 > bn \), para valores de a e b.
O mesmo argumento se aplica aos termos que não são principais. Mesmo se o tempo de execução do algoritmo A fosse n+1000000, ainda seria melhor que o algoritmo B para um valor suficientemente grande de n.
Em geral, esperamos que um algoritmo com um termo principal menor seja um algoritmo melhor para grandes problemas, mas, para problemas menores, pode haver um ponto de desvio onde outro algoritmo seja melhor. A posição do ponto de desvio depende dos detalhes dos algoritmos, das entradas e do hardware; então, ele é normalmente ignorado para os propósitos da análise algorítmica. Porém, isso não significa que você pode se esquecer dele.
Se dois algoritmos tiverem o mesmo termo principal de ordem, é difícil dizer qual é melhor; mais uma vez, a resposta depende dos detalhes. Assim, para a análise algorítmica, funções com o mesmo termo principal são consideradas equivalentes, mesmo se tiverem coeficientes diferentes.
Uma ordem de crescimento é um conjunto de funções cujo comportamento de crescimento é considerado equivalente. Por exemplo, 2n, 100n e n+1 pertencem à mesma ordem de crescimento, que se escreve \( O(n) \) em notação Grande-O e muitas vezes é chamada de linear, porque cada função no conjunto cresce linearmente em relação a n.
Todas as funções com o termo principal \( n^2 \) pertencem a \( O(n^2) \); elas são chamadas de quadráticas.
A tabela seguinte mostra algumas ordens de crescimento mais comuns na análise algorítmica, em ordem crescente de complexidade.
| Ordem de crescimento | Nome |
|---|---|
| \( O(1) \) | constante |
| \( O(\log_b n) \) | logarítmica (para qualquer b) |
| \( O(n) \) | linear |
| \( O(n \log_b n) \) | log-linear |
| \( O(n^2) \) | quadrática |
| \( O(n^3) \) | cúbica |
| \( O(c^n) \) | exponencial (para qualquer c) |
Para os termos logarítmicos, a base do logaritmo não importa; a alteração de bases é o equivalente da multiplicação por uma constante, o que não altera a ordem de crescimento. De forma similar, todas as funções exponenciais pertencem à mesma ordem de crescimento, apesar da base do expoente. As funções exponenciais crescem muito rapidamente, então os algoritmos exponenciais só são úteis para pequenos problemas.
Exercício B.1
Leia a página da Wikipédia sobre a notação Grande-O (Big-Oh notation) em http://en.wikipedia.org/wiki/Big_O_notation e responda às seguintes perguntas:
1. Qual é a ordem de crescimento de \( n^3 + n^2 \)? E de \( 1000000n^3 + n^2 \)? Ou de \( n^3 + 1000000n^2 \)?
2. Qual é a ordem de crescimento de \( (n^2 + n) . (n + 1) \)? Antes de começar a multiplicar, lembre-se de que você só precisa do termo principal.
3. Se f está em \( O(g) \), para alguma função não especificada g, o que podemos dizer de af+b?
4. Se f1 e f2 estão em \( O(g) \), o que podemos dizer a respeito de f1 + f2?
5. Se f1 está em \( O(g) \) e f2 está em \( O(h) \), o que podemos dizer a respeito de f1 + f2?
6. Se f1 está em \( O(g) \) e f2 é O(h) \), o que podemos dizer a respeito de f1 . f2?
Programadores que se preocupam com o desempenho muitas vezes consideram esse tipo de análise difícil de engolir. A razão para isso é: às vezes os coeficientes e os termos não principais fazem muita diferença. Os detalhes do hardware, a linguagem de programação e as características da entrada fazem grande diferença. E para pequenos problemas, o comportamento assintótico é irrelevante.
Porém, se mantiver essas questões em mente, a análise algorítmica pode ser uma ferramenta útil. Pelo menos para grandes problemas, os “melhores” algoritmos são normalmente melhores, e, às vezes, muito melhores. A diferença entre dois algoritmos com a mesma ordem de crescimento é normalmente um fator constante, mas a diferença entre um bom algoritmo e um algoritmo ruim é ilimitada!
B.2 - Análise de operações básicas do Python
No Python, a maior parte das operações aritméticas tem um tempo constante; a multiplicação normalmente leva mais tempo que a adição e a subtração, e a divisão leva até mais tempo, mas esses tempos de execução não dependem da magnitude dos operandos. Os números inteiros muito grandes são uma exceção; nesse caso, o tempo de execução aumenta com o número de dígitos.
Operações de indexação – ler ou escrever elementos em uma sequência ou dicionário – também têm tempo constante, não importa o tamanho da estrutura de dados.
Um loop for que atravesse uma sequência ou dicionário é normalmente linear, desde que todas as operações no corpo do loop sejam de tempo constante. Por exemplo, somar os elementos de uma lista é linear:
total = 0
for x in t:
total += x
A função integrada sum também é linear porque faz a mesma coisa, mas tende a ser mais rápida porque é uma implementação mais eficiente; na linguagem da análise algorítmica, tem um coeficiente principal menor.
Via de regra, se o corpo de um loop está em \( O(na) \), então o loop inteiro está em \( O(na + 1) \). A exceção é se você puder mostrar que o loop encerra depois de um número constante de iterações. Se um loop é executado k vezes, não importa o valor de n, então o loop está em \( O(na) \), mesmo para valores grandes de k.
A multiplicação por k não altera a ordem de crescimento, nem a divisão. Então, se o corpo de um loop está em \( O(na) \) e é executado n/k vezes, o loop está em \( O(na + 1) \), mesmo para valores grandes de k.
A maior parte das operações de strings e tuplas são lineares, exceto a indexação e len, que são de tempo constante. As funções integradas min e max são lineares. O tempo de execução de uma operação de fatia é proporcional ao comprimento da saída, mas não depende do tamanho da entrada.
A concatenação de strings é linear; o tempo de execução depende da soma dos comprimentos dos operandos.
Todos os métodos de string são lineares, mas se os comprimentos das strings forem limitados por uma constante – por exemplo, operações em caracteres únicos – são consideradas de tempo constante. O método de string join é linear; o tempo de execução depende do comprimento total das strings.
A maior parte dos métodos de lista são lineares, mas há algumas exceções:
-
A soma de um elemento ao fim de uma lista é de tempo constante em média; quando o espaço acaba, ela ocasionalmente é copiada a uma posição maior, mas o tempo total de operações n é \( O(n) \), portanto o tempo médio de cada operação é \( O(1) \).
-
A remoção de um elemento do fim de uma lista é de tempo constante.
-
A ordenação é \( O(n \log n) \).
A maior parte das operações e métodos de dicionário são de tempo constante, mas há algumas exceções:
-
O tempo de execução de update é proporcional ao tamanho do dicionário passado como parâmetro, não o dicionário que está sendo atualizado.
-
keys, values e items são de tempo constante porque retornam iteradores. Porém, se fizer um loop pelos iteradores, o loop será linear.
O desempenho de dicionários é um dos milagres menores da ciência da computação. Vemos como funcionam em “Hashtables”, na página 302.
Exercício B.2
Leia a página da Wikipédia sobre algoritmos de ordenação em http://en.wikipedia.org/wiki/Sorting_algorithm e responda às seguintes perguntas:
1. O que é um “tipo de comparação”? Qual é a melhor opção nos casos de pior cenário de ordem de crescimento para um tipo de comparação? Qual é a melhor opção nos casos de pior cenário de ordem de crescimento para qualquer algoritmo de ordenação?
2. Qual é a ordem de crescimento do tipo bolha, e por que Barack Obama acha que “não é a escolha certa”?
3. Qual é a ordem de crescimento do tipo radix? Quais são as precondições necessárias para usá-la?
4. O que é um tipo estável e qual é sua importância na prática?
5. Qual é o pior algoritmo de ordenação (que tenha um nome)?
6. Que algoritmo de ordenação a biblioteca C usa? Que algoritmo de ordenação o Python usa? Esses algoritmos são estáveis? Você pode ter que pesquisar no Google para encontrar essas respostas.
- Muitos dos tipos de não comparação são lineares, então, por que o Python usa um tipo de comparação \( O(n \log n) \)?
B.3 - Análise de algoritmos de busca
Uma busca é um algoritmo que recebe uma coleção e um item de objetivo e determina se o objetivo está na coleção, muitas vezes retornando o índice do objetivo.
O algoritmo de busca mais simples é uma “busca linear”, que atravessa os itens da coleção em ordem, parando se encontrar o objetivo. No pior caso, ele tem que atravessar a coleção inteira, então o tempo de execução é linear.
O operador in para sequências usa uma busca linear; assim como métodos de string como find e count.
Se os elementos da sequência estiverem em ordem, você pode usar uma busca por bisseção, que é \( O(\log n) \). A busca por bisseção é semelhante ao algoritmo que você poderia usar para procurar uma palavra em um dicionário (um dicionário de papel, não a estrutura de dados). Em vez de começar no início e verificar cada item em ordem, você começa com o item do meio e verifica se a palavra que está procurando vem antes ou depois. Se vier antes, então procura na primeira metade da sequência. Se não, procura na segunda metade. Seja como for, você corta o número de itens restantes pela metade.
Se a sequência tiver um milhão de itens, serão necessários cerca de 20 passos para encontrar a palavra ou concluir que não está lá. Então é aproximadamente 50 mil vezes mais rápido que uma busca linear.
A busca por bisseção pode ser muito mais rápida que a busca linear, mas é preciso que a sequência esteja em ordem, o que pode exigir trabalho extra.
Há outra estrutura de dados chamada hashtable, que é até mais rápida – você pode fazer uma busca em tempo constante – e ela não exige que os itens estejam ordenados. Os dicionários do Python são implementados usando hashtables e é por isso a maior parte das operações de dicionário, incluindo o operador in, são de tempo constante.
B.4 - Hashtables
Para explicar como hashtables funcionam e por que o seu desempenho é tão bom, começo com uma implementação simples de um mapa e vou melhorá-lo gradualmente até que seja uma hashtable.
Uso o Python para demonstrar essas implementações, mas, na vida real, eu não escreveria um código como esse no Python; bastaria usar um dicionário! Assim, para o resto deste capítulo, você tem que supor que os dicionários não existem e que quer implementar uma estrutura de dados que faça o mapa de chaves a valores. As operações que precisa implementar são:
add(k, v)
Insere um novo item que mapeia a chave k ao valor v. Com um dicionário de Python, d, essa operação é escrita d[k] = v.
get(k)
Procura e devolve o valor que corresponde à chave k. Com um dicionário de Python, d, esta operação é escrita d[k] ou d.get(k).
Por enquanto, vou supor que cada chave só apareça uma vez. A implementação mais simples desta interface usa uma lista de tuplas, onde cada tupla é um par chave-valor:
class LinearMap:
def __init__(self):
self.items = []
def add(self, k, v):
self.items.append((k, v))
def get(self, k):
for key, val in self.items:
if key == k:
return val
raise KeyError
add acrescenta uma tupla chave-valor à lista de itens, o que tem tempo constante.
get usa um loop for para buscar na lista: se encontrar a chave-alvo, retorna o valor correspondente; do contrário, exibe um KeyError. Então get é linear.
Uma alternativa é manter uma lista ordenada por chaves. Assim, get poderia usar uma busca por bisseção, que é \( O(\log n) \). Porém, inserir um novo item no meio de uma lista é linear, então isso pode não ser a melhor opção. Há outras estruturas de dados que podem implementar add e get em tempo logarítmico, mas isso não é tão bom como tempo constante, então vamos continuar.
Uma forma de melhorar LinearMap é quebrar a lista de pares chave-valor em listas menores. Aqui está uma implementação chamada BetterMap, que é uma lista de cem LinearMaps. Como veremos em um segundo, a ordem de crescimento para get ainda é linear, mas BetterMap é um passo no caminho em direção a hashtables:
class BetterMap:
def __init__(self, n=100):
self.maps = []
for i in range(n):
self.maps.append(LinearMap())
def find_map(self, k):
index = hash(k) % len(self.maps)
return self.maps[index]
def add(self, k, v):
m = self.find_map(k)
m.add(k, v)
def get(self, k):
m = self.find_map(k)
return m.get(k)
__init__ cria uma lista de n LinearMaps.
find_map é usada por add e get para saber em qual mapa o novo item deve ir ou em qual mapa fazer a busca.
find_map usa a função integrada hash, que recebe quase qualquer objeto do Python e retorna um número inteiro. Uma limitação desta implementação é que ela só funciona com chaves hashable. Tipos mutáveis como listas e dicionários não são hashable.
Objetos hashable considerados equivalentes retornam o mesmo valor hash, mas o oposto não é necessariamente verdade: dois objetos com valores diferentes podem retornar o mesmo valor hash.
find_map usa o operador módulo para manter os valores hash no intervalo de 0 a len(self.maps), então o resultado é um índice legal na lista. Naturalmente, isso significa que muitos valores hash diferentes serão reunidos no mesmo índice. Entretanto, se a função hash dispersar as coisas de forma consistente (que é o que as funções hash foram projetadas para fazer), então esperamos ter n/100 itens por LinearMap.
Como o tempo de execução de LinearMap.get é proporcional ao número de itens, esperamos que BetterMap seja aproximadamente cem vezes mais rápido que LinearMap. A ordem de crescimento ainda é linear, mas o coeficiente principal é menor. Isto é bom, mas não tão bom quanto uma hashtable.
Aqui (finalmente) está a ideia crucial que faz hashtables serem rápidas: se puder limitar o comprimento máximo de LinearMaps, LinearMap.get é de tempo constante. Tudo o que você precisa fazer é rastrear o número de itens e quando o número de itens por LinearMap exceder o limite, alterar o tamanho da hashtable acrescentando LinearMaps.
Aqui está uma implementação de uma hashtable:
class HashMap:
def __init__(self):
self.maps = BetterMap(2)
self.num = 0
def get(self, k):
return self.maps.get(k)
def add(self, k, v):
if self.num == len(self.maps.maps):
self.resize()
self.maps.add(k, v)
self.num += 1
def resize(self):
new_maps = BetterMap(self.num * 2)
for m in self.maps.maps:
for k, v in m.items:
new_maps.add(k, v)
self.maps = new_maps
Cada HashMap contém um BetterMap; __init__ inicia com apenas dois LinearMaps e inicializa num, que monitora o número de itens.
get apenas despacha para BetterMap. O verdadeiro trabalho acontece em add, que verifica o número de itens e o tamanho de BetterMap: se forem iguais, o número médio de itens por LinearMap é um, então resize é chamada.
resize faz um novo BetterMap duas vezes maior que o anterior, e então “redispersa” os itens do mapa antigo no novo.
A redispersão é necessária porque alterar o número de LinearMaps muda o denominador do operador módulo em find_map. Isso significa que alguns objetos que costumavam ser dispersos no mesmo LinearMap serão separados (que é o que queríamos, certo?).
A redispersão é linear, então resize é linear, o que pode parecer ruim, já que prometi que add seria de tempo constante. Entretanto, lembre-se de que não temos que alterar o tamanho a cada vez, então add normalmente é de tempo constante e só ocasionalmente linear. O volume total de trabalho para executar add n vezes é proporcional a n, então o tempo médio de cada add é de tempo constante!
Para ver como isso funciona, pense como seria começar com uma HashTable vazia e inserir uma série de itens. Começamos com dois LinearMaps, então as duas primeiras inserções são rápidas (não é necessário alterar o tamanho). Digamos que elas tomem uma unidade do trabalho cada uma. A próxima inserção exige uma alteração de tamanho, então temos de redispersar os dois primeiros itens (vamos chamar isso de mais duas unidades de trabalho) e então acrescentar o terceiro item (mais uma unidade). Acrescentar o próximo item custa uma unidade, então o total, por enquanto, é de seis unidades de trabalho para quatro itens.
O próximo add custa cinco unidades, mas os três seguintes são só uma unidade cada um, então o total é de 14 unidades para as primeiras oito inserções.
O próximo add custa nove unidades, mas então podemos inserir mais sete antes da próxima alteração de tamanho, então o total é de 30 unidades para as primeiras 16 inserções.
Depois de 32 inserções, o custo total é de 62 unidades, e espero que você esteja começando a ver um padrão. Depois de n inserções, nas quais n é uma potência de dois, o custo total é de 2n-2 unidades, então o trabalho médio por inserção é um pouco menos de duas unidades. Quando n é uma potência de dois, esse é o melhor caso; para outros valores de n, o trabalho médio é um pouco maior, mas isso não é importante. O importante é que seja \( O(1) \).
A Figura 21.1 mostra graficamente como isso funciona. Cada bloco representa uma unidade de trabalho. As colunas mostram o trabalho total para cada inserção na ordem da esquerda para a direita: os primeiros dois adds custam uma unidade, o terceiro custa três unidades etc.
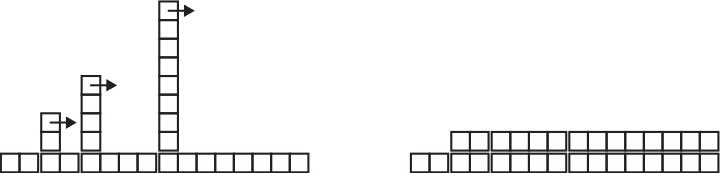 .
.
Figura B.1 – O custo de inserções em uma hashtable.
O trabalho extra de redispersão aparece como uma sequência de torres cada vez mais altas com um aumento de espaço entre elas. Agora, se derrubar as torres, espalhando o custo de alterar o tamanho por todas as inserções, poderá ver graficamente que o custo total depois de n inserções é de 2n − 2.
Uma característica importante deste algoritmo é que quando alteramos o tamanho da HashTable, ela cresce geometricamente; isto é, multiplicamos o tamanho por uma constante. Se você aumentar o tamanho aritmeticamente – somando um número fixo de cada vez – o tempo médio por add é linear.
Você pode baixar minha implementação de HashMap em http://thinkpython2.com/code/Map.py, mas lembre-se de que não há razão para usá-la; se quiser um mapa, basta usar um dicionário do Python.
B.5 - Glossário
análise de algoritmos
Forma de comparar algoritmos quanto às suas exigências de espaço e/ou tempo de execução.
modelo de máquina
Representação simplificada de um computador usada para descrever algoritmos.
pior caso
Entrada que faz um dado algoritmo rodar mais lentamente (ou exigir mais espaço).
termo principal
Em um polinômio, o termo com o expoente mais alto.
ponto de desvio
Tamanho do problema em que dois algoritmos exigem o mesmo tempo de execução ou espaço.
ordem de crescimento
Conjunto de funções em que todas crescem em uma forma considerada equivalente para os propósitos da análise de algoritmos. Por exemplo, todas as funções que crescem linearmente pertencem à mesma ordem de crescimento.
notação Grande-O (Big-Oh notation)
Notação para representar uma ordem de crescimento; por exemplo, \( O(n) \) representa o conjunto de funções que crescem linearmente.
linear
Algoritmo cujo tempo de execução é proporcional ao tamanho do problema, pelo menos para grandes tamanhos de problema.
quadrático
Algoritmo cujo tempo de execução é proporcional a \( n^2 \), onde n é uma medida de tamanho do problema.
busca
Problema de localizar um elemento de uma coleção (como uma lista ou dicionário) ou de decidir que não está presente.
hashtable
Estrutura de dados que representa uma coleção de pares chave-valor e executa buscas em tempo constante.
[1] popen foi descartado, ou seja, devemos parar de usá-lo e começar a usar o módulo subprocess. Entretanto, para casos simples, eu considero subprocess mais complicado que o necessário. Então vou continuar usando popen até que o removam.
[2] Mas se fizerem uma pergunta como essa em uma entrevista, creio que a melhor resposta é “A forma mais rápida de classificar um milhão de números inteiros é usar qualquer função de ordenação oferecida pela linguagem que estou usando. Se o desempenho é bom o suficiente para a grande maioria das aplicações, mas a minha aplicação acabasse sendo lenta demais, eu usaria algum recurso para investigar onde o tempo está sendo gasto. Se parecesse que um algoritmo mais rápido teria um efeito significativo sobre o desempenho, então procuraria uma boa implementação do tipo radix”.
Colofão
O animal na capa de Pense em Python é um papagaio-da-carolina, também conhecido como periquito-da-carolina (Conuropsis carolinensis). Este papagaio habitava o sudeste dos Estados Unidos e foi o único papagaio continental a habitar regiões acima do norte do México. Um dia, vivia no norte, em locais tão distantes quanto Nova Iorque e os Grandes Lagos, embora fosse encontrado principalmente na região da Flórida às Carolinas.
O papagaio-da-carolina era quase todo verde com a cabeça amarela e, na maturidade, tinha uma coloração laranja na testa e na face. Seu tamanho médio variava de 31 a 33 cm. Tinha uma voz alta, ruidosa e palrava constantemente enquanto se alimentava. Habitava troncos de árvores ocos perto de brejos e barrancos. O papagaio-da-carolina era um animal muito gregário, que vivia em pequenos grupos os quais podiam chegar a várias centenas quando se alimentavam.
Infelizmente, essas áreas de alimentação muitas vezes eram as plantações de agricultores, que disparavam nos pássaros para mantê-los longe das plantas. A natureza social dos pássaros fazia com que eles voassem ao resgate de qualquer papagaio ferido, permitindo aos agricultores derrubar bandos inteiros de cada vez. Além disso, suas penas eram usadas para embelezar chapéus de senhoras, e alguns papagaios eram mantidos como mascotes. Uma combinação desses fatores levou o papagaio-da-carolina a tornar-se raro no fim dos anos 1800, e as doenças de aves domésticas podem ter contribuído para diminuir seu número. Pelos anos 1920, a espécie estava extinta.
Hoje, há mais de 700 espécimes de papagaios-da-carolina conservados em museus no mundo inteiro.
Muitos dos animais nas capas de livros da O’Reilly estão em perigo de extinção; todos eles são importantes para o mundo. Para saber mais sobre como você pode ajudar, acesse animals.oreilly.com. A imagem da capa é do livro Johnson’s Natural History.
Sobre o autor
Allen Downey é professor de Ciência da Computação no Olin College of Engineering. Ele já ensinou no Wellesley College, Colby College e na U.C. Berkeley. É doutor em Ciência da Computação pela U.C. Berkeley e mestre e graduado pelo MIT.
