Pense em Python

7.5 - Raízes quadradas

Loops muitas vezes são usados em programas que calculam resultados numéricos, começando com uma resposta aproximada e melhorando-a iterativamente.

Por exemplo, uma forma de calcular raízes quadradas é o método de Newton. Suponha que você queira saber a raiz quadrada de a. Se começar com quase qualquer estimativa, x, é possível calcular uma estimativa melhor com a seguinte fórmula:

.

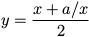Por exemplo, se a for 4 e x for 3:
>>> a = 4
>>> x = 3
>>> y = (x + a/x) / 2
>>> y
2.16666666667

O resultado é mais próximo à resposta correta (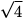. = 2). Se repetirmos o processo com a nova estimativa, chegamos ainda mais perto:

>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00641025641

Depois de algumas atualizações, a estimativa é quase exata:

>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00001024003
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.00000000003

Em geral, não sabemos com antecedência quantos passos são necessários para chegar à resposta correta, mas sabemos quando chegamos lá porque a estimativa para de mudar:

>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.0
>>> x = y
>>> y = (x + a/x) / 2
>>> y
2.0

Quando y == x, podemos parar. Aqui está um loop que começa com uma estimativa inicial, x, e a melhora até que deixe de mudar:

while True:
    print(x)
    y = (x + a/x) / 2
    if y == x:
        break
    x = y

Para a maior parte de valores de a funciona bem, mas pode ser perigoso testar a igualdade de um float. Os valores de ponto flutuante são aproximadamente corretos: a maioria dos números racionais, como 1/3, e números irracionais, como 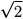., não podem ser representados exatamente com um float.

Em vez de verificar se x e y são exatamente iguais, é mais seguro usar a função integrada abs para calcular o valor absoluto ou magnitude da diferença entre eles:

if abs(y-x) < epsilon:
    break

Onde epsilon tem um valor como 0.0000001, que determina a proximidade desejada entre x e y.