6.5 - Mais recursividade
Cobrimos apenas um pequeno subconjunto do Python, mas talvez seja bom você saber que este subconjunto é uma linguagem de programação completa, ou seja, qualquer coisa que possa ser calculada pode ser expressa nesta linguagem. Qualquer programa que já foi escrito pode ser reescrito apenas com os recursos da linguagem que você aprendeu até agora (na verdade, seria preciso alguns comandos para dispositivos de controle como mouse, discos etc., mas isso é tudo).
Comprovar esta declaração é um exercício nada trivial realizado pela primeira vez por Alan Turing, um dos primeiros cientistas da computação (alguns diriam que ele foi matemático, mas muitos dos primeiros cientistas da computação começaram como matemáticos). Assim, é conhecida como a Tese de Turing. Para uma exposição mais completa (e exata) da Tese de Turing, recomendo o livro de Michael Sipser, Introduction to the Theory of Computation (Introdução à teoria da computação, Course Technology, 2012).
Para dar uma ideia do que podemos fazer com as ferramentas que aprendeu até agora, avaliaremos algumas funções matemáticas definidas recursivamente. Uma definição recursiva é semelhante a uma definição circular, no sentido de que a definição contém uma referência à coisa que é definida. Uma definição realmente circular não é muito útil:
vorpal
Adjetivo usado para descrever algo que é vorpal.
Ver uma definição assim no dicionário pode ser irritante. Por outro lado, se procurar a definição da função de fatorial, denotada pelo símbolo !, você pode encontrar algo assim:
0! = 1
n! = n·(n − 1)!
Esta definição diz que o fatorial de 0 é 1, e o fatorial de qualquer outro valor, n, é n multiplicado pelo fatorial de n-1.
Então 3! é 3 vezes 2!, que é 2 vezes 1!, que é 1 vez 0!. Juntando tudo, 3! é igual a 3 vezes 2 vezes 1 vezes 1, que é 6.
Se puder escrever uma definição recursiva de algo, você poderá escrever um programa em Python que a avalie. O primeiro passo deve ser decidir quais parâmetros ela deve ter. Neste caso, deve estar claro que factorial recebe um número inteiro:
def factorial(n):
Se o argumento for 0, tudo que temos de fazer é retornar 1:
def factorial(n):
if n == 0:
return 1
Senão, e aí é que fica interessante, temos que fazer uma chamada recursiva para encontrar o fatorial de n-1 e então multiplicá-lo por n:
def factorial(n):
if n == 0:
return 1
else:
recurse = factorial(n-1)
result = n * recurse
return result
O fluxo de execução deste programa é semelhante ao fluxo de countdown em “Recursividade”, na página 81. Se chamarmos factorial com o valor 3:
Como 3 não é 0, tomamos o segundo ramo e calculamos o fatorial de n-1...
Como 2 não é 0, tomamos o segundo ramo e calculamos o fatorial de n-1...
Como 1 não é 0, tomamos o segundo ramo e calculamos o fatorial de n-1...
Como 0 é igual a 0, tomamos o primeiro ramo e devolvemos 1 sem fazer mais chamadas recursivas.
O valor de retorno, 1, é multiplicado por n, que é 1, e o resultado é devolvido.
O valor de retorno, 1, é multiplicado por n, que é 2, e o resultado é devolvido.
O valor devolvido (2) é multiplicado por n, que é 3, e o resultado, 6, torna-se o valor devolvido pela chamada de função que começou o processo inteiro.
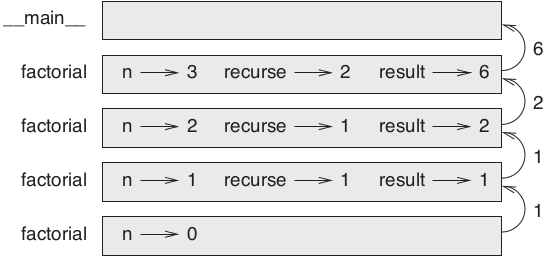
A Figura 6.1 mostra como é o diagrama da pilha para esta sequência de chamadas de função.
 .
.
Figura 6.1 – Diagrama da pilha para factorial.
Os valores devolvidos são mostrados ao serem passados de volta até o alto da pilha. Em cada frame, o valor devolvido é o valor de result, que é o produto de n e recurse.
No último frame, as variáveis locais recurse e result não existem, porque o ramo que os cria não é executado.