Apêndice B: Análise de algoritmos

Este apêndice é um excerto editado de Think Complexity, por Allen B. Downey, também publicado pela O’Reilly Media (2012). Depois de ler este livro aqui, pode ser uma boa ideia lê-lo também.

Análise de algoritmos é um ramo da Ciência da Computação que estuda o desempenho de algoritmos, especialmente suas exigências de tempo de execução e requisitos de espaço. Veja http://en.wikipedia.org/wiki/Analysis_of_algorithms.

A meta prática da análise de algoritmos é prever o desempenho de algoritmos diferentes para guiar decisões de projeto.

Durante a campanha presidencial dos Estados Unidos de 2008, pediram ao candidato Barack Obama para fazer uma entrevista de emprego improvisada quando visitou a Google. O diretor executivo, Eric Schmidt, brincou, pedindo a ele “a forma mais eficiente de classificar um milhão de números inteiros de 32 bits”. Aparentemente, Obama tinha sido alertado porque respondeu na hora: “Creio que a ordenação por bolha (bubble sort) não seria a escolha certa”. Veja http://bit.ly/1MpIwTf.

Isso é verdade: a ordenação por bolha é conceitualmente simples, mas lenta para grandes conjuntos de dados. A resposta que Schmidt procurava provavelmente é “ordenação radix” (radix sort)[2].

A meta da análise de algoritmos é fazer comparações significativas entre algoritmos, mas há alguns problemas:

O desempenho relativo dos algoritmos pode depender de características do hardware; então um algoritmo pode ser mais rápido na Máquina A, e outro na Máquina B. A solução geral para este problema é especificar um modelo de máquina e analisar o número de passos ou operações que um algoritmo exige sob um modelo dado.
O desempenho relativo pode depender dos detalhes do conjunto de dados. Por exemplo, alguns algoritmos de ordenação rodam mais rápido se os dados já foram parcialmente ordenados; outros algoritmos rodam mais devagar neste caso. Uma forma comum de evitar este problema é analisar o pior caso. Às vezes é útil analisar o desempenho de casos médios, mas isso é normalmente mais difícil, e pode não ser óbvio qual conjunto de casos deve ser usado para a média.
O desempenho relativo também depende do tamanho do problema. Um algoritmo de ordenação que é rápido para pequenas listas pode ser lento para longas listas. A solução habitual para este problema é expressar o tempo de execução (ou o número de operações) como uma função do tamanho de problema e funções de grupo em categorias que dependem de sua velocidade de crescimento quando o tamanho de problema aumenta.

Uma coisa boa sobre este tipo de comparação é que ela é própria para a classificação simples de algoritmos. Por exemplo, se souber que o tempo de execução do algoritmo A tende a ser proporcional ao tamanho da entrada n, e o algoritmo B tende a ser proporcional a \( n^2 \), então espero que A seja mais rápido que B, pelo menos para valores grandes de n.

Esse tipo de análise tem algumas desvantagens, mas falaremos disso mais adiante.

B.1 - Ordem de crescimento

Vamos supor que você analisou dois algoritmos e expressou seus tempos de execução em relação ao tamanho da entrada: o algoritmo A leva 100n+1 passos para resolver um problema com o tamanho n; o algoritmo B leva \( n^2 + n + 1 \) passos.

A tabela seguinte mostra o tempo de execução desses algoritmos para tamanhos de problema diferentes:


Tamanho da entrada	Tempo de execução do algoritmo A	Tempo de execução do algoritmo B
10	1 001	111
100	10 001	10 101
1 000	100 001	1 001 001
10 000	1 000 001	> 1010

Ao chegar em n=10, o algoritmo A parece bem ruim; ele é quase dez vezes mais longo que o algoritmo B. No entanto, para n=100 eles são bem parecidos, e, para valores maiores, A é muito melhor.

A razão fundamental é que para grandes valores de n, qualquer função que contenha um termo \( n^2 \) será mais rápida que uma função cujo termo principal seja n. O termo principal é o que tem o expoente mais alto.

Para o algoritmo A, o termo principal tem um grande coeficiente, 100, que é a razão de B ser melhor que A para um valor pequeno de n. Entretanto, apesar dos coeficientes, sempre haverá algum valor de n em que \( an^2 > bn \), para valores de a e b.

O mesmo argumento se aplica aos termos que não são principais. Mesmo se o tempo de execução do algoritmo A fosse n+1000000, ainda seria melhor que o algoritmo B para um valor suficientemente grande de n.

Em geral, esperamos que um algoritmo com um termo principal menor seja um algoritmo melhor para grandes problemas, mas, para problemas menores, pode haver um ponto de desvio onde outro algoritmo seja melhor. A posição do ponto de desvio depende dos detalhes dos algoritmos, das entradas e do hardware; então, ele é normalmente ignorado para os propósitos da análise algorítmica. Porém, isso não significa que você pode se esquecer dele.

Se dois algoritmos tiverem o mesmo termo principal de ordem, é difícil dizer qual é melhor; mais uma vez, a resposta depende dos detalhes. Assim, para a análise algorítmica, funções com o mesmo termo principal são consideradas equivalentes, mesmo se tiverem coeficientes diferentes.

Uma ordem de crescimento é um conjunto de funções cujo comportamento de crescimento é considerado equivalente. Por exemplo, 2n, 100n e n+1 pertencem à mesma ordem de crescimento, que se escreve \( O(n) \) em notação Grande-O e muitas vezes é chamada de linear, porque cada função no conjunto cresce linearmente em relação a n.

Todas as funções com o termo principal \( n^2 \) pertencem a \( O(n^2) \); elas são chamadas de quadráticas.

A tabela seguinte mostra algumas ordens de crescimento mais comuns na análise algorítmica, em ordem crescente de complexidade.

Ordem de crescimento	Nome
\( O(1) \)	constante
\( O(\log_b n) \)	logarítmica (para qualquer b)
\( O(n) \)	linear
\( O(n \log_b n) \)	log-linear
\( O(n^2) \)	quadrática
\( O(n^3) \)	cúbica
\( O(c^n) \)	exponencial (para qualquer c)

Para os termos logarítmicos, a base do logaritmo não importa; a alteração de bases é o equivalente da multiplicação por uma constante, o que não altera a ordem de crescimento. De forma similar, todas as funções exponenciais pertencem à mesma ordem de crescimento, apesar da base do expoente. As funções exponenciais crescem muito rapidamente, então os algoritmos exponenciais só são úteis para pequenos problemas.

Exercício B.1

Leia a página da Wikipédia sobre a notação Grande-O (Big-Oh notation) em http://en.wikipedia.org/wiki/Big_O_notation e responda às seguintes perguntas:

1. Qual é a ordem de crescimento de \( n^3 + n^2 \)? E de \( 1000000n^3 + n^2 \)? Ou de \( n^3 + 1000000n^2 \)?

2. Qual é a ordem de crescimento de \( (n^2 + n) . (n + 1) \)? Antes de começar a multiplicar, lembre-se de que você só precisa do termo principal.

3. Se f está em \( O(g) \), para alguma função não especificada g, o que podemos dizer de af+b?

4. Se f1 e f2 estão em \( O(g) \), o que podemos dizer a respeito de f1 + f2?

5. Se f1 está em \( O(g) \) e f2 está em \( O(h) \), o que podemos dizer a respeito de f1 + f2?

6. Se f1 está em \( O(g) \) e f2 é O(h) \), o que podemos dizer a respeito de f1 . f2?

Programadores que se preocupam com o desempenho muitas vezes consideram esse tipo de análise difícil de engolir. A razão para isso é: às vezes os coeficientes e os termos não principais fazem muita diferença. Os detalhes do hardware, a linguagem de programação e as características da entrada fazem grande diferença. E para pequenos problemas, o comportamento assintótico é irrelevante.

Porém, se mantiver essas questões em mente, a análise algorítmica pode ser uma ferramenta útil. Pelo menos para grandes problemas, os “melhores” algoritmos são normalmente melhores, e, às vezes, muito melhores. A diferença entre dois algoritmos com a mesma ordem de crescimento é normalmente um fator constante, mas a diferença entre um bom algoritmo e um algoritmo ruim é ilimitada!

B.2 - Análise de operações básicas do Python

No Python, a maior parte das operações aritméticas tem um tempo constante; a multiplicação normalmente leva mais tempo que a adição e a subtração, e a divisão leva até mais tempo, mas esses tempos de execução não dependem da magnitude dos operandos. Os números inteiros muito grandes são uma exceção; nesse caso, o tempo de execução aumenta com o número de dígitos.

Operações de indexação – ler ou escrever elementos em uma sequência ou dicionário – também têm tempo constante, não importa o tamanho da estrutura de dados.

Um loop for que atravesse uma sequência ou dicionário é normalmente linear, desde que todas as operações no corpo do loop sejam de tempo constante. Por exemplo, somar os elementos de uma lista é linear:

total = 0
for x in t:
    total += x

A função integrada sum também é linear porque faz a mesma coisa, mas tende a ser mais rápida porque é uma implementação mais eficiente; na linguagem da análise algorítmica, tem um coeficiente principal menor.

Via de regra, se o corpo de um loop está em \( O(na) \), então o loop inteiro está em \( O(na + 1) \). A exceção é se você puder mostrar que o loop encerra depois de um número constante de iterações. Se um loop é executado k vezes, não importa o valor de n, então o loop está em \( O(na) \), mesmo para valores grandes de k.

A multiplicação por k não altera a ordem de crescimento, nem a divisão. Então, se o corpo de um loop está em \( O(na) \) e é executado n/k vezes, o loop está em \( O(na + 1) \), mesmo para valores grandes de k.

A maior parte das operações de strings e tuplas são lineares, exceto a indexação e len, que são de tempo constante. As funções integradas min e max são lineares. O tempo de execução de uma operação de fatia é proporcional ao comprimento da saída, mas não depende do tamanho da entrada.

A concatenação de strings é linear; o tempo de execução depende da soma dos comprimentos dos operandos.

Todos os métodos de string são lineares, mas se os comprimentos das strings forem limitados por uma constante – por exemplo, operações em caracteres únicos – são consideradas de tempo constante. O método de string join é linear; o tempo de execução depende do comprimento total das strings.

A maior parte dos métodos de lista são lineares, mas há algumas exceções:

A soma de um elemento ao fim de uma lista é de tempo constante em média; quando o espaço acaba, ela ocasionalmente é copiada a uma posição maior, mas o tempo total de operações n é \( O(n) \), portanto o tempo médio de cada operação é \( O(1) \).
A remoção de um elemento do fim de uma lista é de tempo constante.
A ordenação é \( O(n \log n) \).

A maior parte das operações e métodos de dicionário são de tempo constante, mas há algumas exceções:

O tempo de execução de update é proporcional ao tamanho do dicionário passado como parâmetro, não o dicionário que está sendo atualizado.
keys, values e items são de tempo constante porque retornam iteradores. Porém, se fizer um loop pelos iteradores, o loop será linear.

O desempenho de dicionários é um dos milagres menores da ciência da computação. Vemos como funcionam em “Hashtables”, na página 302.

Exercício B.2

Leia a página da Wikipédia sobre algoritmos de ordenação em http://en.wikipedia.org/wiki/Sorting_algorithm e responda às seguintes perguntas:

1. O que é um “tipo de comparação”? Qual é a melhor opção nos casos de pior cenário de ordem de crescimento para um tipo de comparação? Qual é a melhor opção nos casos de pior cenário de ordem de crescimento para qualquer algoritmo de ordenação?

2. Qual é a ordem de crescimento do tipo bolha, e por que Barack Obama acha que “não é a escolha certa”?

3. Qual é a ordem de crescimento do tipo radix? Quais são as precondições necessárias para usá-la?

4. O que é um tipo estável e qual é sua importância na prática?

5. Qual é o pior algoritmo de ordenação (que tenha um nome)?

6. Que algoritmo de ordenação a biblioteca C usa? Que algoritmo de ordenação o Python usa? Esses algoritmos são estáveis? Você pode ter que pesquisar no Google para encontrar essas respostas.

Muitos dos tipos de não comparação são lineares, então, por que o Python usa um tipo de comparação \( O(n \log n) \)?

B.3 - Análise de algoritmos de busca

Uma busca é um algoritmo que recebe uma coleção e um item de objetivo e determina se o objetivo está na coleção, muitas vezes retornando o índice do objetivo.

O algoritmo de busca mais simples é uma “busca linear”, que atravessa os itens da coleção em ordem, parando se encontrar o objetivo. No pior caso, ele tem que atravessar a coleção inteira, então o tempo de execução é linear.

O operador in para sequências usa uma busca linear; assim como métodos de string como find e count.

Se os elementos da sequência estiverem em ordem, você pode usar uma busca por bisseção, que é \( O(\log n) \). A busca por bisseção é semelhante ao algoritmo que você poderia usar para procurar uma palavra em um dicionário (um dicionário de papel, não a estrutura de dados). Em vez de começar no início e verificar cada item em ordem, você começa com o item do meio e verifica se a palavra que está procurando vem antes ou depois. Se vier antes, então procura na primeira metade da sequência. Se não, procura na segunda metade. Seja como for, você corta o número de itens restantes pela metade.

Se a sequência tiver um milhão de itens, serão necessários cerca de 20 passos para encontrar a palavra ou concluir que não está lá. Então é aproximadamente 50 mil vezes mais rápido que uma busca linear.

A busca por bisseção pode ser muito mais rápida que a busca linear, mas é preciso que a sequência esteja em ordem, o que pode exigir trabalho extra.

Há outra estrutura de dados chamada hashtable, que é até mais rápida – você pode fazer uma busca em tempo constante – e ela não exige que os itens estejam ordenados. Os dicionários do Python são implementados usando hashtables e é por isso a maior parte das operações de dicionário, incluindo o operador in, são de tempo constante.

B.4 - Hashtables

Para explicar como hashtables funcionam e por que o seu desempenho é tão bom, começo com uma implementação simples de um mapa e vou melhorá-lo gradualmente até que seja uma hashtable.

Uso o Python para demonstrar essas implementações, mas, na vida real, eu não escreveria um código como esse no Python; bastaria usar um dicionário! Assim, para o resto deste capítulo, você tem que supor que os dicionários não existem e que quer implementar uma estrutura de dados que faça o mapa de chaves a valores. As operações que precisa implementar são:

add(k, v)

Insere um novo item que mapeia a chave k ao valor v. Com um dicionário de Python, d, essa operação é escrita d[k] = v.

get(k)

Procura e devolve o valor que corresponde à chave k. Com um dicionário de Python, d, esta operação é escrita d[k] ou d.get(k).

Por enquanto, vou supor que cada chave só apareça uma vez. A implementação mais simples desta interface usa uma lista de tuplas, onde cada tupla é um par chave-valor:

class LinearMap:

    def __init__(self):
        self.items = []

    def add(self, k, v):
        self.items.append((k, v))

    def get(self, k):
        for key, val in self.items:
            if key == k:
                return val
        raise KeyError

add acrescenta uma tupla chave-valor à lista de itens, o que tem tempo constante.

get usa um loop for para buscar na lista: se encontrar a chave-alvo, retorna o valor correspondente; do contrário, exibe um KeyError. Então get é linear.

Uma alternativa é manter uma lista ordenada por chaves. Assim, get poderia usar uma busca por bisseção, que é \( O(\log n) \). Porém, inserir um novo item no meio de uma lista é linear, então isso pode não ser a melhor opção. Há outras estruturas de dados que podem implementar add e get em tempo logarítmico, mas isso não é tão bom como tempo constante, então vamos continuar.

Uma forma de melhorar LinearMap é quebrar a lista de pares chave-valor em listas menores. Aqui está uma implementação chamada BetterMap, que é uma lista de cem LinearMaps. Como veremos em um segundo, a ordem de crescimento para get ainda é linear, mas BetterMap é um passo no caminho em direção a hashtables:

class BetterMap:

    def __init__(self, n=100):
        self.maps = []
        for i in range(n):
            self.maps.append(LinearMap())

    def find_map(self, k):
        index = hash(k) % len(self.maps)
        return self.maps[index]

    def add(self, k, v):
        m = self.find_map(k)
        m.add(k, v)

    def get(self, k):
        m = self.find_map(k)
        return m.get(k)

__init__ cria uma lista de n LinearMaps.

find_map é usada por add e get para saber em qual mapa o novo item deve ir ou em qual mapa fazer a busca.

find_map usa a função integrada hash, que recebe quase qualquer objeto do Python e retorna um número inteiro. Uma limitação desta implementação é que ela só funciona com chaves hashable. Tipos mutáveis como listas e dicionários não são hashable.

Objetos hashable considerados equivalentes retornam o mesmo valor hash, mas o oposto não é necessariamente verdade: dois objetos com valores diferentes podem retornar o mesmo valor hash.

find_map usa o operador módulo para manter os valores hash no intervalo de 0 a len(self.maps), então o resultado é um índice legal na lista. Naturalmente, isso significa que muitos valores hash diferentes serão reunidos no mesmo índice. Entretanto, se a função hash dispersar as coisas de forma consistente (que é o que as funções hash foram projetadas para fazer), então esperamos ter n/100 itens por LinearMap.

Como o tempo de execução de LinearMap.get é proporcional ao número de itens, esperamos que BetterMap seja aproximadamente cem vezes mais rápido que LinearMap. A ordem de crescimento ainda é linear, mas o coeficiente principal é menor. Isto é bom, mas não tão bom quanto uma hashtable.

Aqui (finalmente) está a ideia crucial que faz hashtables serem rápidas: se puder limitar o comprimento máximo de LinearMaps, LinearMap.get é de tempo constante. Tudo o que você precisa fazer é rastrear o número de itens e quando o número de itens por LinearMap exceder o limite, alterar o tamanho da hashtable acrescentando LinearMaps.

Aqui está uma implementação de uma hashtable:

class HashMap:
    def __init__(self):
        self.maps = BetterMap(2)
        self.num = 0
    def get(self, k):
        return self.maps.get(k)
    def add(self, k, v):
        if self.num == len(self.maps.maps):
            self.resize()
        self.maps.add(k, v)
        self.num += 1
    def resize(self):
        new_maps = BetterMap(self.num * 2)
        for m in self.maps.maps:
            for k, v in m.items:
                new_maps.add(k, v)
        self.maps = new_maps

Cada HashMap contém um BetterMap; __init__ inicia com apenas dois LinearMaps e inicializa num, que monitora o número de itens.

get apenas despacha para BetterMap. O verdadeiro trabalho acontece em add, que verifica o número de itens e o tamanho de BetterMap: se forem iguais, o número médio de itens por LinearMap é um, então resize é chamada.

resize faz um novo BetterMap duas vezes maior que o anterior, e então “redispersa” os itens do mapa antigo no novo.

A redispersão é necessária porque alterar o número de LinearMaps muda o denominador do operador módulo em find_map. Isso significa que alguns objetos que costumavam ser dispersos no mesmo LinearMap serão separados (que é o que queríamos, certo?).

A redispersão é linear, então resize é linear, o que pode parecer ruim, já que prometi que add seria de tempo constante. Entretanto, lembre-se de que não temos que alterar o tamanho a cada vez, então add normalmente é de tempo constante e só ocasionalmente linear. O volume total de trabalho para executar add n vezes é proporcional a n, então o tempo médio de cada add é de tempo constante!

Para ver como isso funciona, pense como seria começar com uma HashTable vazia e inserir uma série de itens. Começamos com dois LinearMaps, então as duas primeiras inserções são rápidas (não é necessário alterar o tamanho). Digamos que elas tomem uma unidade do trabalho cada uma. A próxima inserção exige uma alteração de tamanho, então temos de redispersar os dois primeiros itens (vamos chamar isso de mais duas unidades de trabalho) e então acrescentar o terceiro item (mais uma unidade). Acrescentar o próximo item custa uma unidade, então o total, por enquanto, é de seis unidades de trabalho para quatro itens.

O próximo add custa cinco unidades, mas os três seguintes são só uma unidade cada um, então o total é de 14 unidades para as primeiras oito inserções.

O próximo add custa nove unidades, mas então podemos inserir mais sete antes da próxima alteração de tamanho, então o total é de 30 unidades para as primeiras 16 inserções.

Depois de 32 inserções, o custo total é de 62 unidades, e espero que você esteja começando a ver um padrão. Depois de n inserções, nas quais n é uma potência de dois, o custo total é de 2n-2 unidades, então o trabalho médio por inserção é um pouco menos de duas unidades. Quando n é uma potência de dois, esse é o melhor caso; para outros valores de n, o trabalho médio é um pouco maior, mas isso não é importante. O importante é que seja \( O(1) \).

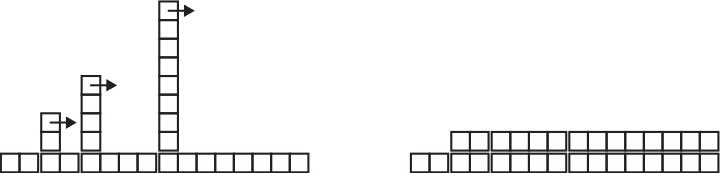
A Figura 21.1 mostra graficamente como isso funciona. Cada bloco representa uma unidade de trabalho. As colunas mostram o trabalho total para cada inserção na ordem da esquerda para a direita: os primeiros dois adds custam uma unidade, o terceiro custa três unidades etc.

.
Figura B.1 – O custo de inserções em uma hashtable.

O trabalho extra de redispersão aparece como uma sequência de torres cada vez mais altas com um aumento de espaço entre elas. Agora, se derrubar as torres, espalhando o custo de alterar o tamanho por todas as inserções, poderá ver graficamente que o custo total depois de n inserções é de 2n − 2.

Uma característica importante deste algoritmo é que quando alteramos o tamanho da HashTable, ela cresce geometricamente; isto é, multiplicamos o tamanho por uma constante. Se você aumentar o tamanho aritmeticamente – somando um número fixo de cada vez – o tempo médio por add é linear.

Você pode baixar minha implementação de HashMap em http://thinkpython2.com/code/Map.py, mas lembre-se de que não há razão para usá-la; se quiser um mapa, basta usar um dicionário do Python.

B.5 - Glossário

análise de algoritmos

Forma de comparar algoritmos quanto às suas exigências de espaço e/ou tempo de execução.

modelo de máquina

Representação simplificada de um computador usada para descrever algoritmos.

pior caso

Entrada que faz um dado algoritmo rodar mais lentamente (ou exigir mais espaço).

termo principal

Em um polinômio, o termo com o expoente mais alto.

ponto de desvio

Tamanho do problema em que dois algoritmos exigem o mesmo tempo de execução ou espaço.

ordem de crescimento

Conjunto de funções em que todas crescem em uma forma considerada equivalente para os propósitos da análise de algoritmos. Por exemplo, todas as funções que crescem linearmente pertencem à mesma ordem de crescimento.

notação Grande-O (Big-Oh notation)

Notação para representar uma ordem de crescimento; por exemplo, \( O(n) \) representa o conjunto de funções que crescem linearmente.

linear

Algoritmo cujo tempo de execução é proporcional ao tamanho do problema, pelo menos para grandes tamanhos de problema.

quadrático

Algoritmo cujo tempo de execução é proporcional a \( n^2 \), onde n é uma medida de tamanho do problema.

busca

Problema de localizar um elemento de uma coleção (como uma lista ou dicionário) ou de decidir que não está presente.

hashtable

Estrutura de dados que representa uma coleção de pares chave-valor e executa buscas em tempo constante.

[1] popen foi descartado, ou seja, devemos parar de usá-lo e começar a usar o módulo subprocess. Entretanto, para casos simples, eu considero subprocess mais complicado que o necessário. Então vou continuar usando popen até que o removam.

[2] Mas se fizerem uma pergunta como essa em uma entrevista, creio que a melhor resposta é “A forma mais rápida de classificar um milhão de números inteiros é usar qualquer função de ordenação oferecida pela linguagem que estou usando. Se o desempenho é bom o suficiente para a grande maioria das aplicações, mas a minha aplicação acabasse sendo lenta demais, eu usaria algum recurso para investigar onde o tempo está sendo gasto. Se parecesse que um algoritmo mais rápido teria um efeito significativo sobre o desempenho, então procuraria uma boa implementação do tipo radix”.

Pense em Python